最优化&线代
梯度
- Jacobian矩阵
简单理解为多个实函数偏导组成的矩阵。
梯度向量是特殊的Jacobian矩阵。 - Hessian矩阵
多个实函数的二阶偏导数矩阵。
Jacobian矩阵的导数是Hessian矩阵。- 多元函数极值判断
- Hessian矩阵负定:极大值;
- Hessian矩阵正定:极小值;
- Hessian矩阵不定:非极值;
- Hessian矩阵半正定或者半负定:需进一步判断;
- 多元函数极值判断
最优化方法
- 梯度下降法
- 牛顿法
在求函数 y = c o s ( x ) y=cos(x) y=cos(x)在区间 x ∈ [ 0 , 2 π ] x \in [0,2\pi] x∈[0,2π]的极小值点时,如果初始值取 0 0 0或者 2 π 2\pi 2π一阶导为 0 0 0,会停止于极大值。
线代
- 正交
python 中实现Schmidt正交
from sympy.matrices import Matrix,GramSchmidt
L = [Matrix([1,2,3]), Matrix([2,1,3]), Matrix([3,2,1])]
o1=GramSchmidt(L)
o2=GramSchmidt(L,True) #标准化
- 行列式
行列式可以理解为衡量向量变化程度。一维长度,二维面积,三维体积,以此类推。
概率论与数理统计
估计
- 最大似然估计(频率派)
假设参数是一个数 - 贝叶斯估计(贝叶斯派)
假设参数是一个随机变量- 为什么要用贝叶斯估计?
- 解决小数据问题
- 处理不确定性(增加先验)
- 进行模型压缩
- 不足
P ( D ) P(D) P(D)难以计算,可以用采样近似估计,因此计算量很大
- 为什么要用贝叶斯估计?
作业
Rosenbrockh函数
f
(
x
)
=
(
a
−
x
1
)
2
+
b
(
x
2
−
x
1
2
)
2
f(x)=(a-x_1)^2+b(x_2-x_1^2)^2
f(x)=(a−x1)2+b(x2−x12)2,
其中
x
=
(
x
1
,
x
2
)
T
∈
R
2
\mathbf{x}=( x_1,x_2)^T\in \mathbf{R}^2
x=(x1,x2)T∈R2,
a
,
b
∈
R
a,b\in R
a,b∈R。
1. 为不同a,b取值,绘制函数三维图像
代码如下:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import time
from mpl_toolkits.mplot3d import Axes3D
class Rosenbrock():
def __init__(self,a0,b0):
self.x1 = np.arange(-1, 1, 0.01)
self.x2 = np.arange(-1, 1, 0.01)
self.a = a0
self.b = b0
self.z = np.square(self.a - self.x1) + self.b * np.square(self.x2 - np.square(self.x1))
# 绘图
def plot(self):
x1, x2 = np.meshgrid(self.x1, self.x2)
z = np.square(self.a - x1) + self.b * np.square(x2 - np.square(x1))
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(x1, x2, z, alpha=1, cmap='rainbow') # 生成表面, alpha 用于控制透明度
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f')
plt.title('a='+ str(self.a) + ', b=' + str(self.b))
plt.show()
if __name__ == '__main__':
a= [-100,0,100]
b = [-100,0,100]
for i in a:
for j in b:
r = Rosenbrock(i,j)
r.plot()
运行结果如下:
| (a,b) | b ∈ ( − ∞ , 0 ) b\in (-\infty,0) b∈(−∞,0) | b = 0 b=0 b=0 | b ∈ ( 0 , + ∞ ) b\in (0,+\infty) b∈(0,+∞) |
|---|---|---|---|
| a ∈ ( − ∞ , 0 ) a\in (-\infty,0) a∈(−∞,0) | 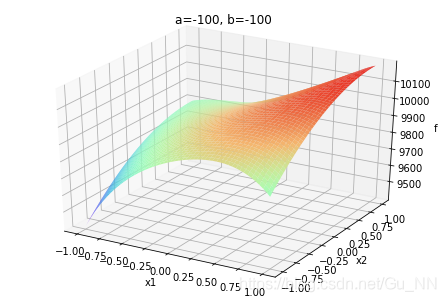 | 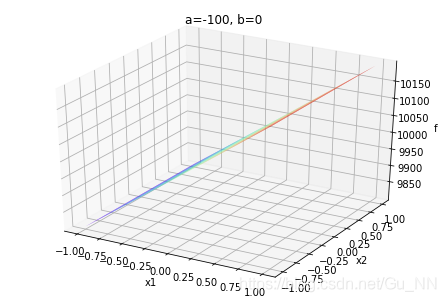 | 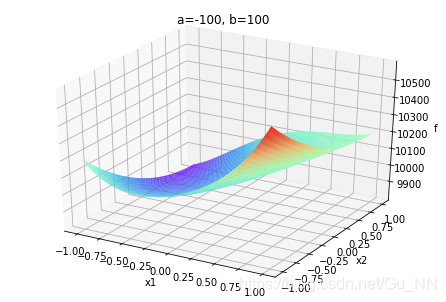 |
| a = 0 a=0 a=0 | 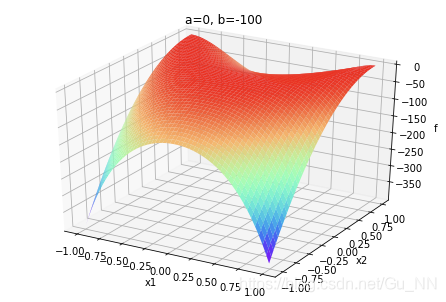 | .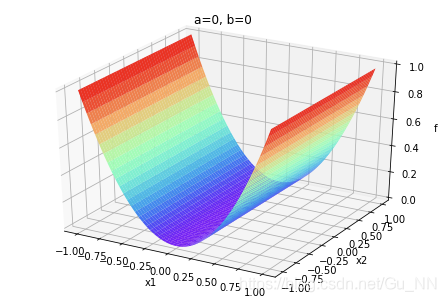 | 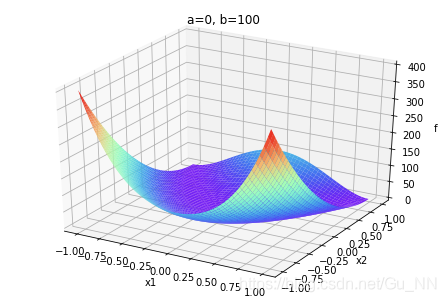 |
| a ∈ ( 0 , + ∞ ) a\in (0,+\infty) a∈(0,+∞) | 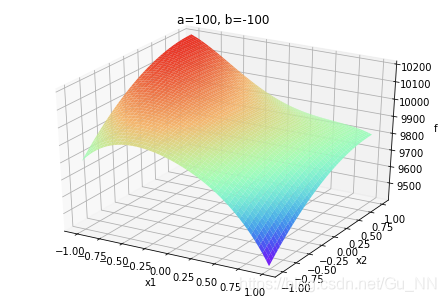 | 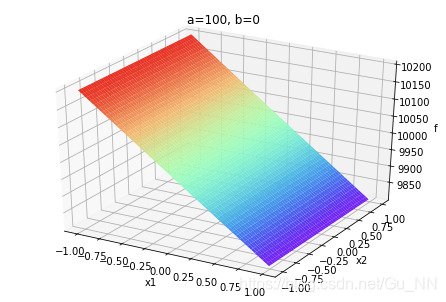 | 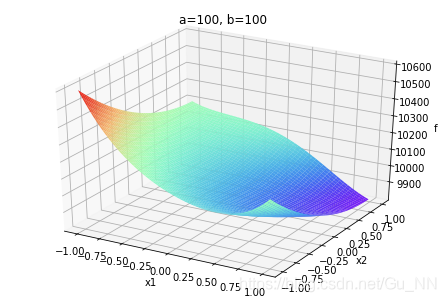 |
a,b不同取值对函数有很大影响。
注:为快速计算,图中
x
1
,
x
2
∈
(
−
1
,
1
)
x_1,x_2\in(-1,1)
x1,x2∈(−1,1),当取值范围不同时,图像会不同
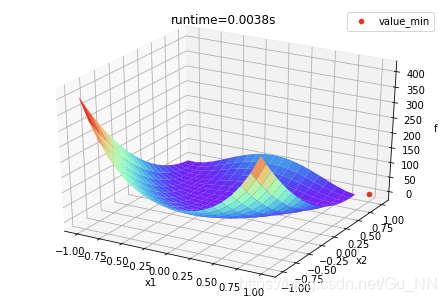
2. 寻找全局最小值及最小解,并在图中标注,分析时空复杂度,计算运行时间
最优化方法为牛顿法。以a = 1,b = 100为例,代码如下:
def rosenbrockfunc(x1,x2,a,b):
return np.square(a - x1) + b * np.square(x2 - np.square(x1))
def H(x1, x2,a,b):
return np.array([[12 * b * x1 * x1 - 4 * b * x2 + 2, -4 * b * x1],
[-4 * b * x1, 2 * b]])
def grad(x1, x2, a, b):
return np.array([[2 * x1 - 2 * a + 4 * b * x1 * (x1 * x1 - x2)],
[2 * b * (x2 - x1 * x1)]])
def rosenbrock_nt_plot(rb,min_x1,min_x2,min_z,runtime):
x1, x2 = np.meshgrid(rb.x1, rb.x2)
z = np.square(rb.a - x1) + rb.b * np.square(x2 - np.square(x1))
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(x1, x2, z, alpha=1, cmap='rainbow')
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f')
ax.scatter(min_x1,min_x2,min_z,c= 'r',label='value_min')
plt.legend()
plt.title('runtime='+ str(round(runtime,4)) + 's')
plt.show()
r = Rosenbrock(1,100)
times = 100
#初始值
rand_init = np.random.randint(0,r.z.shape[0])
x1_init,x2_init = r.x1[rand_init],r.x2[rand_init]
x0 =np.array([x1_init,x2_init]).reshape((-1,1))
answers = []
min_z = rosenbrockfunc(x1_init,x2_init,1,100)
min_x1 = x1_init
min_x2 = x2_init
#开始计时
start_time = time.time()
for t in range(times):
a = r.a
b = r.b
xi = x0 - np.matmul(np.linalg.inv(H(x1_init, x2_init,a,b)),grad(x1_init, x2_init, a, b).reshape((-1,1)))
x0 = xi
x1_init = x0[0,0]
x2_init = x0[1,0]
answers.append(x0)
z = rosenbrockfunc(x1_init,x2_init,1,100)
if z<min_z:
min_z = z
min_x1 = x1_init
min_x2 = x2_init
end_time = time.time() #结束计时
running_time = end_time-start_time
#画图
rosenbrock_nt_plot(r,min_x1,min_x2,min_z,running_time)
结果如下:最小解为(1,1),最小值为0。





















 15万+
15万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








