Leetcode 63. Unique Paths II

最新推荐文章于 2024-07-26 10:47:39 发布

GoodJobJasper

最新推荐文章于 2024-07-26 10:47:39 发布

阅读量247

点赞数

CC 4.0 BY-SA版权

分类专栏： Leetcode 文章标签： dfs dp recursion

本文链接：https://blog.youkuaiyun.com/GoodJobJasper/article/details/113306572

Leetcode 专栏收录该内容

278 篇文章

订阅专栏

这篇博客探讨了两种方法来解决带有障碍物的唯一路径问题。方法1采用深度优先搜索（DFS），时间复杂度和空间复杂度均为O(mn)，其中m和n分别为网格的行数和列数。方法2则使用动态规划，同样以O(mn)的时间复杂度解决问题，并可通过优化降低空间复杂度。博客提供了详细的代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

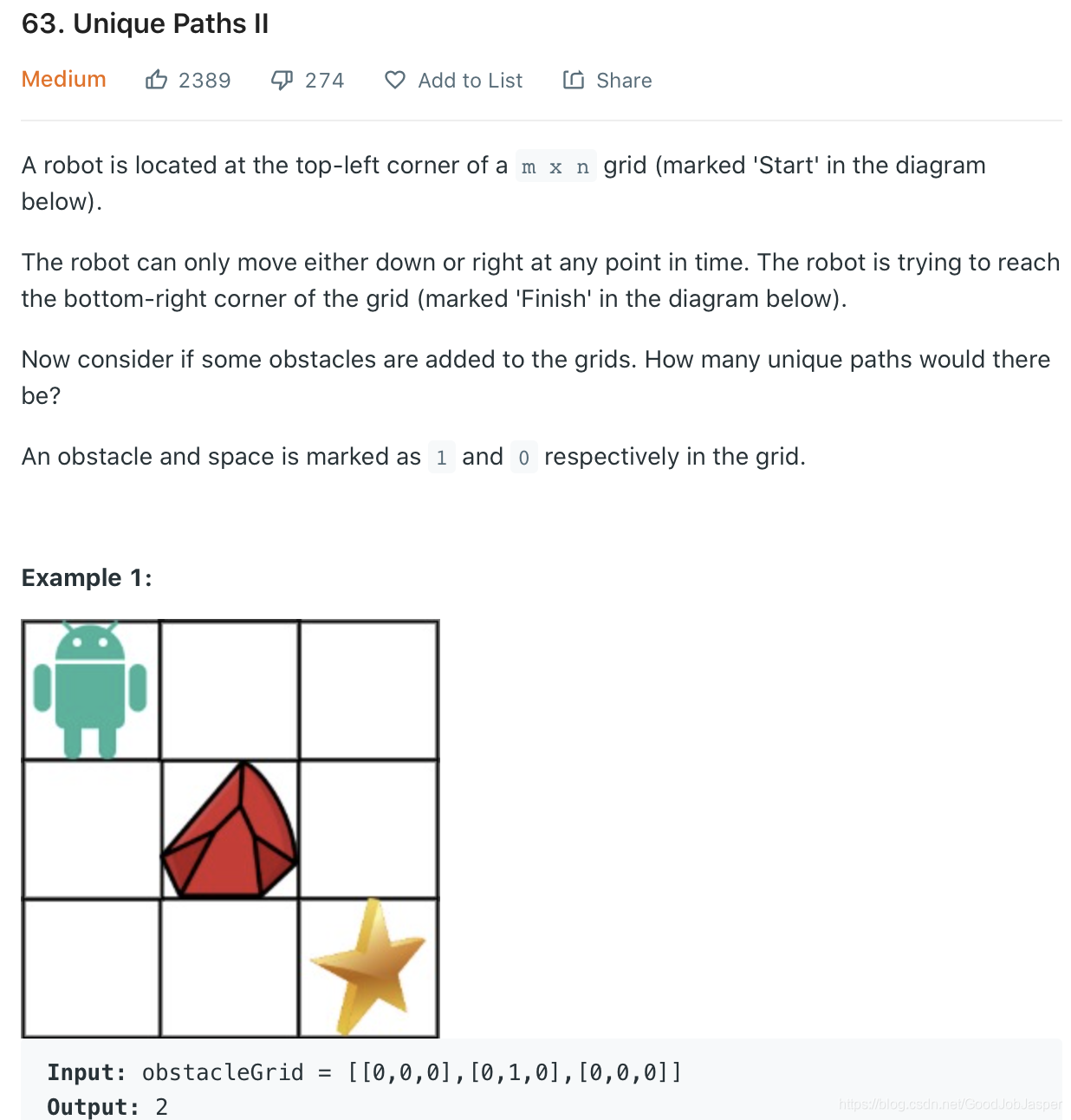
在这里插入图片描述
方法1: 这个很自然第一个想到的肯定是backtracking/dfs。我一开始是想就套用backtracking模版来写的，但是好像不是特别合适，感觉直接dfs就可以了。但是一定要用那个backtracking模版来做的话也可以，可以看下这个链接。下面我直接展示dfs的做法。时间复杂mn，空间复杂mn。

class Solution {
    int m;
    int n;
    Map<Pair<Integer, Integer>, Integer> map = new HashMap<>();
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        this.m = obstacleGrid.length;
        this.n = obstacleGrid[0].length;
        return backtracking(obstacleGrid, new Pair<>(0,0));
    }
    
    public int backtracking(int[][] obstacleGrid, Pair<Integer, Integer> start){
        if(map.containsKey(start)) return map.get(start);
        int row = start.getKey();
        int col = start.getValue();
        if(row >= m || col >= n || obstacleGrid[row][col] == 1) return 0;
        if(row == m - 1 && col == n - 1) return 1;
        int res = backtracking(obstacleGrid, new Pair<>(row + 1, col)) + backtracking(obstacleGrid, new Pair<>(row, col + 1));
        map.put(start, res);
        return res;
    }
}

方法2: dp，时间复杂mn，空间复杂mn。dp的思路完全和62题一模一样，只是遇到阻碍的时候dp数组直接设置为0。当然我们也可以把空间复杂降为1，不新建dp数组，直接在原数组上修改数字就行。具体思路参考lc官方解答。

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m + 1][n + 1];
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                if(obstacleGrid[i - 1][j - 1] == 1){
                   dp[i][j] = 0;
                } else{
                    if(i == 1 && j == 1) dp[i][j] = 1;
                    else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
        return dp[m][n];
    }
}