Leetcode 130. Surrounded Regions

最新推荐文章于 2023-12-01 14:27:39 发布

原创最新推荐文章于 2023-12-01 14:27:39 发布 · 207 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#dfs #bfs #matrix

Leetcode 专栏收录该内容

278 篇文章

订阅专栏

这篇博客介绍了两种方法，深度优先搜索（DFS）和广度优先搜索（BFS），来解决二维字符矩阵的问题。对于给定的棋盘，DFS从边界开始将'O'标记为'E'，然后将未访问的'O'标记为'X'。BFS通过构建边界细胞列表，标记逃逸的细胞，最后更新所有'O'和'E'的状态。两种方法的时间复杂度均为O(mn)，空间复杂度也为O(mn)。

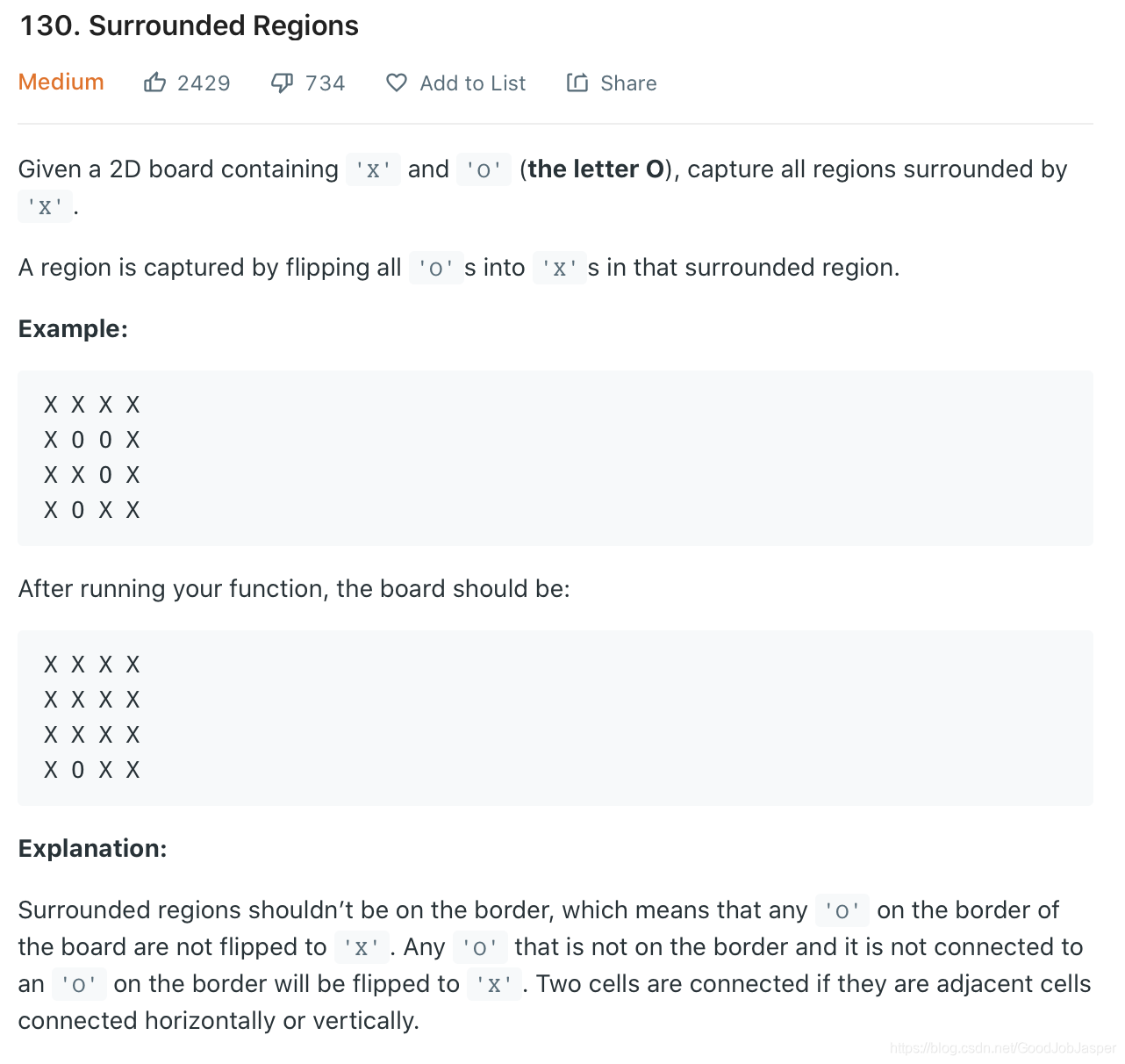
在这里插入图片描述
方法1: dfs。和lc官方解答1思路基本一样。时间复杂mn，空间复杂mn。

class Solution {
    int m;
    int n;
    Set<Pair<Integer,Integer>> set = new HashSet<>();
    public void solve(char[][] board) {
        m = board.length;
        if(m == 0) return;
        n= board[0].length;
        if(m < 3 || n < 3) return;
        // first row and last row
        for(int i = 0; i < m; i += m-1){
            for(int j = 0; j < n; j++){
                if(board[i][j] == 'O'){
                    dfs(board, i, j);
                }
            }
        } 
        
        // first col and last col
        for(int i = 1; i < m - 1; i++){
            for(int j = 0; j < n; j += n-1){
                if(board[i][j] == 'O'){
                    dfs(board, i, j);
                }
            }
        } 
        
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(!set.contains(new Pair(i,j)))
                    board[i][j] = 'X';
            }
        }
    }
    
    public void dfs(char[][] board, int i, int j){
        if(i < 0 || j < 0 || i >= m || j >= n || board[i][j] != 'O' || set.contains(new Pair(i,j))) return;
        set.add(new Pair(i,j));
        dfs(board, i-1, j);
        dfs(board, i+1, j);
        dfs(board, i, j-1);
        dfs(board, i, j+1);
    }
}

方法2: bfs。也不是很难，详细bfs分析一定要去lc去看官方解答2，写得很好。时间复杂mn，空间复杂mn。


public class Solution {
  protected Integer ROWS = 0;
  protected Integer COLS = 0;

  public void solve(char[][] board) {
    if (board == null || board.length == 0) {
      return;
    }
    this.ROWS = board.length;
    this.COLS = board[0].length;

    List<Pair<Integer, Integer>> borders = new LinkedList<Pair<Integer, Integer>>();
    // Step 1). construct the list of border cells
    for (int r = 0; r < this.ROWS; ++r) {
      borders.add(new Pair(r, 0));
      borders.add(new Pair(r, this.COLS - 1));
    }
    for (int c = 0; c < this.COLS; ++c) {
      borders.add(new Pair(0, c));
      borders.add(new Pair(this.ROWS - 1, c));
    }

    // Step 2). mark the escaped cells
    for (Pair<Integer, Integer> pair : borders) {
      this.BFS(board, pair.first, pair.second);
    }

    // Step 3). flip the cells to their correct final states
    for (int r = 0; r < this.ROWS; ++r) {
      for (int c = 0; c < this.COLS; ++c) {
        if (board[r][c] == 'O')
          board[r][c] = 'X';
        if (board[r][c] == 'E')
          board[r][c] = 'O';
      }
    }
  }

  protected void BFS(char[][] board, int r, int c) {
    LinkedList<Pair<Integer, Integer>> queue = new LinkedList<Pair<Integer, Integer>>();
    queue.offer(new Pair<>(r, c));

    while (!queue.isEmpty()) {
      Pair<Integer, Integer> pair = queue.pollFirst();
      int row = pair.first, col = pair.second;
      if (board[row][col] != 'O')
        continue;

      board[row][col] = 'E';
      if (col < this.COLS - 1)
        queue.offer(new Pair<>(row, col + 1));
      if (row < this.ROWS - 1)
        queue.offer(new Pair<>(row + 1, col));
      if (col > 0)
        queue.offer(new Pair<>(row, col - 1));
      if (row > 0)
        queue.offer(new Pair<>(row - 1, col));
    }
  }
}


class Pair<U, V> {
  public U first;
  public V second;

  public Pair(U first, V second) {
    this.first = first;
    this.second = second;
  }
}