272. Closest Binary Search Tree Value II

最新推荐文章于 2022-02-02 22:15:19 发布

原创最新推荐文章于 2022-02-02 22:15:19 发布 · 179 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#bst #dfs #sort #heap #quick select

Leetcode 专栏收录该内容

278 篇文章

订阅专栏

博客介绍了在BST中查找k个最接近元素的三种方法。方法1是中序遍历加排序，时间复杂度nlogn，空间复杂度n；方法2是中序遍历加堆，时间复杂度nlogk，空间复杂度n + k，也有不用堆的巧妙方法；方法3是快速选择，时间复杂度n，空间复杂度n。

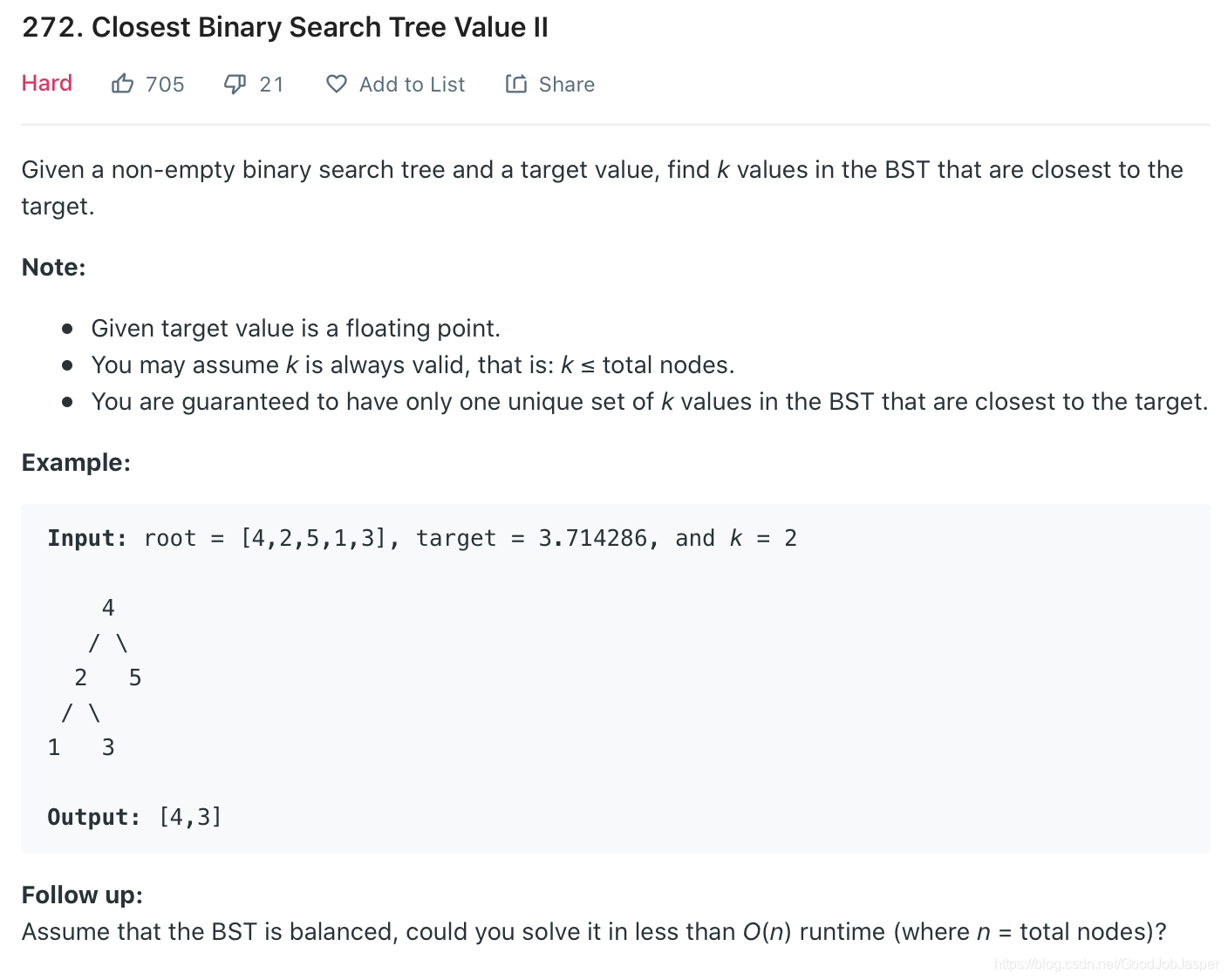
在这里插入图片描述
方法1: inorder traversal + sort（override）。时间复杂nlogn，空间复杂n。

class Solution {
    public void inorder(TreeNode root, List<Integer> nums) {
        if (root == null) return;
        inorder(root.left, nums);
        nums.add(root.val);
        inorder(root.right, nums);
    }

    public List<Integer> closestKValues(TreeNode root, double target, int k) {
        List<Integer> nums = new ArrayList();
        inorder(root, nums);
        
        Collections.sort(nums, new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return Math.abs(o1 - target) < Math.abs(o2 - target) ? -1 : 1;
            }
        });
        return nums.subList(0, k);
    }
}

方法2: inorder traversal + heap. 这个heap将会 keep less close element first的规则，heap规定大小为k。所以我们遍历bst。每当heap满的时候我们需要判断是不是要把当前node加进heap（拿当前node大小与heap第一个元素大小比较，heap第一个元素就是与target差距最大的元素）。时间复杂nlogk。空间复杂n+k。

class Solution {
    public void inorder(TreeNode r, List<Integer> nums, Queue<Integer> heap, int k) {
        if (r == null) 
            return;
                    
        inorder(r.left, nums, heap, k);
        heap.add(r.val);
        if (heap.size() > k) 
            heap.remove();
        inorder(r.right, nums, heap, k);
    }

    public List<Integer> closestKValues(TreeNode root, double target, int k) {
        List<Integer> nums = new ArrayList();
        
        // init heap 'less close element first'
        Queue<Integer> heap = new PriorityQueue<>((o1, o2) -> Math.abs(o1 - target) > Math.abs(o2 - target) ? -1 : 1);
        inorder(root, nums, heap, k);
        return new ArrayList<>(heap);
    }
}

这个方法二也可以不用heap，但是这个方法非常的巧妙，要自己画图才知道为啥行得通，但是一般情况下都是要用heap的，因为要找到那个与target差距最大的元素。下面这个算法时间复杂n，空间复杂h。

public class Solution {
    public List<Integer> closestKValues(TreeNode root, double target, int k) {
        LinkedList<Integer> res = new LinkedList<>();
        collect(root, target, k, res);
        return res;
    }

    public void collect(TreeNode root, double target, int k, LinkedList<Integer> res) {
        if (root == null) return;
        collect(root.left, target, k, res);

        if (res.size() == k) {
            //if size k, add curent and remove head if it's optimal, otherwise return
            if (Math.abs(target - root.val) < Math.abs(target - res.peekFirst())) 
                res.removeFirst();
            else return;
        }
        res.add(root.val);
        collect(root.right, target, k, res);
    }
}