Leetcode 220 Contains Duplicate III

最新推荐文章于 2025-12-28 17:52:30 发布

原创最新推荐文章于 2025-12-28 17:52:30 发布 · 168 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #java #array #BST #treeset

Leetcode 专栏收录该内容

278 篇文章

订阅专栏

本文深入探讨了解决LeetCode中Almost Duplicate问题的三种核心方法：暴力破解、自平衡二叉搜索树及桶排序策略。通过对比不同算法的优劣，帮助读者理解数据结构在算法设计中的关键作用。

在这里插入图片描述
思路一： 这是我自己的思路，其实本质上和approach1是差不多的，brute force。但是会tle。下面给出代码，但是复盘不建议看我的代码，没意义，后面介绍的两种方法才是这道题真正让我学习到的东西：

class Solution {
    public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
        Map[] map = new Map[nums.length];
        for(int i = 0; i < nums.length; i++){
            map[i] = new HashMap();
        }
        
        for(int i = 0; i < nums.length; i++){
            if(map[0].isEmpty())
                map[0].put(0,nums[0]);
            else{
                int flag = 0;
                for(int j = 0; j < i; j++){
                    if(map[j].isEmpty()) break;
                    long a = (int)map[j].get(map[j].keySet().toArray()[0]);
                    long b = nums[i];
                    long num = a - b;
                    num = Math.abs(num);
                    if(num <= t){
                        map[j].put(i,nums[i]);
                        flag = 1;
                    }
                }
                if(flag == 0)
                    map[i].put(i,nums[i]);
            }
        }
        
        for(Map m : map){
            if(m.isEmpty())
                continue;
            else{
                for(int i = 0; i < m.size() - 1; i++){
                    int check = (int)m.keySet().toArray()[i + 1] - (int)m.keySet().toArray()[i];
                    if(check <= k)
                        return true;
                }
            }
        }
        return false;
    }
}

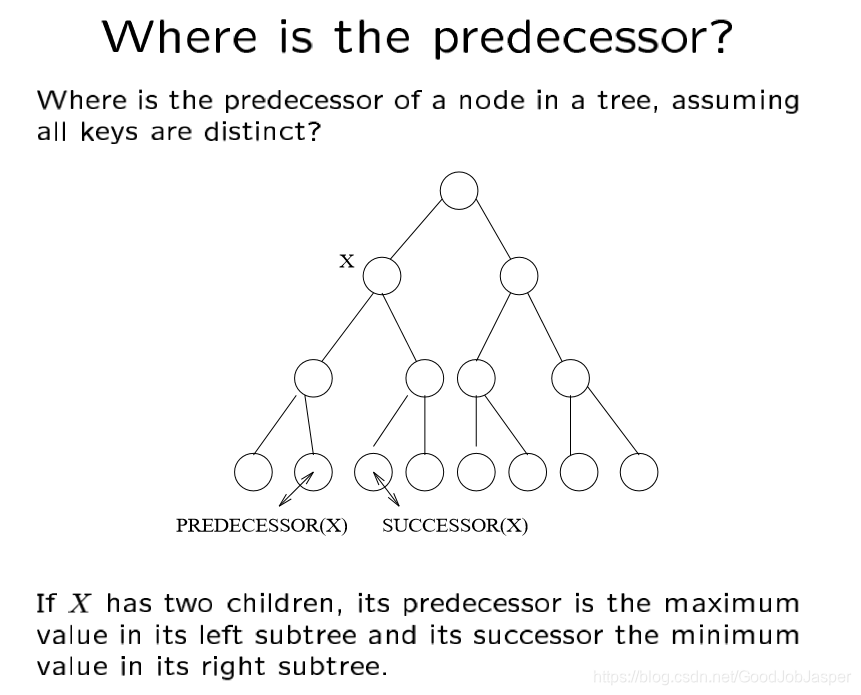
思路二： 利用自平衡二叉寻找树这个数据结构。自平衡二叉寻找树在java中的实现是treeset，这题主要是利用了treeset的两个函数ceiling和floor。floor(E e) 方法返回在这个集合中小于或者等于给定元素的最大元素，如果不存在这样的元素,返回null。ceiling(E e) 方法返回在这个集合中大于或者等于给定元素的最小元素，如果不存在这样的元素,返回null。floor返回的值可以看作e的predecessor，ceiling返回的值可以看作e的successor。关于predecessor和successor在自平衡二叉树种的体现可以参照下面这张图：
在这里插入图片描述
具体这个方法的思路我建议去lc上看approach2，讲的很清楚，这边我直接上代码,其实直接看代码也基本可以看的懂：

public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
    TreeSet<Integer> set = new TreeSet<>();
    for (int i = 0; i < nums.length; ++i) {
        // Find the successor of current element
        Integer s = set.ceiling(nums[i]);
        if (s != null && s <= nums[i] + t) return true;

        // Find the predecessor of current element
        Integer g = set.floor(nums[i]);
        if (g != null && nums[i] <= g + t) return true;

        set.add(nums[i]);
        if (set.size() > k) {
            set.remove(nums[i - k]);
        }
    }
    return false;
}

思路三： buckets。就是按照t的大小来分组，每个组大小都是t。并且每个组只能最多存在一个数字。遍历数组，我们碰到一个数字n，那么要符合题目condition2的数字只可能出现在n所在的组，或n前面一个组，或n后面一个组。我们只要分别check就行，check成功就返回true。同时我们还需要满足condition1，所以当遍历到下标超过k的数字时，我们就要去掉前面最老的一个元素。保证在map中的元素总量小于等于k。我讲的很笼统我建议去lc看approach3讲解，讲的很清楚，这边我直接展示代码：

public class Solution {
    // Get the ID of the bucket from element value x and bucket width w
    // In Java, `-3 / 5 = 0` and but we need `-3 / 5 = -1`.
    private long getID(long x, long w) {
        return x < 0 ? (x + 1) / w - 1 : x / w;
    }

    public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
        if (t < 0) return false;
        Map<Long, Long> d = new HashMap<>();
        long w = (long)t + 1;
        for (int i = 0; i < nums.length; ++i) {
            long m = getID(nums[i], w);
            // check if bucket m is empty, each bucket may contain at most one element
            if (d.containsKey(m))
                return true;
            // check the neighbor buckets for almost duplicate
            if (d.containsKey(m - 1) && Math.abs(nums[i] - d.get(m - 1)) < w)
                return true;
            if (d.containsKey(m + 1) && Math.abs(nums[i] - d.get(m + 1)) < w)
                return true;
            // now bucket m is empty and no almost duplicate in neighbor buckets
            d.put(m, (long)nums[i]);
            if (i >= k) d.remove(getID(nums[i - k], w));
        }
        return false;
    }
}

总结：

自平衡二叉寻找树是bst的升级，它保证了每一个节点的左子树和右子树的height差在1之内。换句话说就是对于自平衡二叉寻找树的任意一个节点，他的balance factor只能为0，1，-1三者之一。为什么要尽量减少这种heights的差距呢，因为bst中的绝大多数操作的耗时时常都与这棵树height有着直接的关系，我们尽量平衡这个bst的话，那么这个bst的height就会减小，对于这个树的操作所花的时间就会越少。
自平衡二叉寻找树的java是现实treeset。
这道题目值得仔细看每个解法，我上面写的思路解释真的很差，因为我现在很饿，我要去吃饭了，建议复盘的时候直接看lc思路解释。