贝叶斯

2019.10

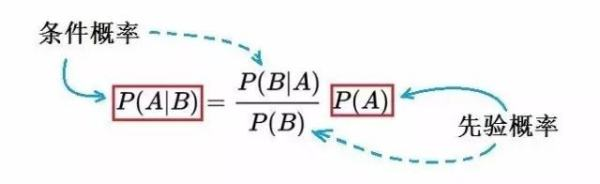
贝叶斯解释图

P(A)是先验概率，求法：

• 经验判断
• 估计
• 有监督学习

P(B)先验概率，全概率公式 P(B)=P(B|A)P(A)+P(B|A1')P(A1')+...

P(B|A)类条件概率，连续型用似然估计类条件概率密度。

P(A|B)为后验概率，表示某事在某类别发生的概率。

 

eg:A为性别，B为患病。

P(A|B)=P(A)P(B|A)/P(B)，求患者为女性概率

P(A)男女比例用经验或者估计

P(B|A)女性患者概率，概率估计

P(B)人口患病概率

https://blog.youkuaiyun.com/To_be_to_thought/article/details/81223561讲贝叶斯和贝叶斯公式的，里面推荐了几个数据书。

https://blog.youkuaiyun.com/u014683535/article/details/51872093#re.split讲python正则化的

 

设A为某事，B某类别。

P（A|B）=P(AB)/P(B)

=P(A)P(B|A)/P(B)

=P(A)P(B|A)/SUM(P(An)P(B|An))

B相当于约束，非B发生了A发生的概率，非先后关系。表约束，在B的前提下，A发生的概率。

 

监督学习

监督学习生成的模型有两种：

1决策模型Y=P(X)，判别方法

由数据直接学习f(X)或条件概率P(Y|X)作为预测模型，判别方法关心的是给定X，应预测什么样的输出Y，典型有k邻近算法。

2条件概率模型P(Y|X)，生成方法

由数据学习联合概率分布P(AB)，求条件概率P(Y|X)作为预测的模型。模型表示给定输入X，产生输出Y的生成关系。典型有朴素贝叶斯和隐形马尔可夫模型。

----------------------------------------------------------------------------------------------------------------------------------------------------------------------

先验概率是指根据以往经验和分析得到的概率，如全概率公式，它往往作为"由因求果"问题中的"因"出现的概率。

在贝叶斯统计推断中，不确定数量的先验概率分布是在考虑一些因素之前表达对这一数量的置信程度的概率分布。例如，先验概率分布可能代表在将来的选举中投票给特定政治家的选民相对比例的概率分布。未知的数量可以是模型的参数或者是潜在变量。

后验概率是信息理论的基本概念之一。在一个通信系统中，在收到某个消息之后，接收端所了解到的该消息发送的概率称为后验概率。

后验概率的计算要以先验概率为基础。后验概率可以根据通过贝叶斯公式，用先验概率和似然函数计算出来。

 

先验概率的分类

1、利用过去历史资料计算得到的先验概率，称为客观先验概率；

2、当历史资料无从取得或资料不完全时，凭人们的主观经验来判断而得到的先验概率，称为主观先验概率。

先验概率的条件

先验概率是通过古典概率模型加以定义的，故又称为古典概率。古典概率模型要求满足两个条件：

1、试验的所有可能结果是有限的；

2、每一种可能结果出现的可能性(概率)相等。若所有可能结果的总数为N，随机事件A包括n个可能结果，那么随机事件A出现的概率为n/N。

先验概率不是根据有关自然状态的全部资料测定的，而只是利用现有的材料(主要是历史资料)计算的；后验概率使用了有关自然状态更加全面的资料，既有先验概率资料，也有补充资料；

先验概率的计算比较简单，没有使用贝叶斯公式；而后验概率的计算，要使用贝叶斯公式，而且在利用样本资料计算逻辑概率时，还要使用理论概率分布，需要更多的数理统计知识。

朴素贝叶斯

编译出现的错误

trainingSet=range(50)——>trainingSet=list(range(50))

gbk’ codec can’t decode byte 0xae in position 199: illegal multibyte sequen 错误

email->ham->23.txt 文本中出现了“?”字符,删去

unexpected EOF while parsing

print少括号了吧

 

利用贝叶斯对文章分类

朴素贝叶斯思路：

train：人工进行特征属性划分，得到先验概率

          机器计算类条件概率，训练生成分类器

test：求和（先验概率*类条件概率），不需要除..，因为都一样；得到后验概率，孰大为孰

import numpy as np
import math
import random
def loadDataSet():
    postingList=[['my','dog','has','flea','problems','help','please'],
                 ['maybe','not','take','him','to','dog','park','stdpid'],
                 ['my','dalmation','is','so','cute','I','love','him'],
                 ['stop','posting','stupid','worthless','garbage'],
                 ['mr','licks','ate','my','steak','how','to','stop','him'],
                 ['quit','buying','worthless','dog','food','stupid']]
    classVec=[0,1,0,1,0,1]
    return postingList,classVec
def createCabList(dataSet):   #将上函数内的列表转化为一个不重复的集合
    vocabSet=set([])    #建立空集合
    for document in dataSet:
        vocabSet=vocabSet|set(document)   #并集
    return list(vocabSet)
def setOfWodrs2Vec(vocabList,inputSet):  #所有单词集合（在createcablist return的）；一篇文章单词（loaddataset的）
    returnVec=[0]*len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)]+=1
        else:
            print("the word:",word,"is not in my vocabulary!")
    return returnVec

#p1vect   p(wn|c1)   {  ,  ,  ,, }每个侮辱性词汇在所有文档（其实就是侮辱性文档）中所有侮辱性词汇总数的占比
#p0vec    p(wn|c0)   {}每个非侮辱性词汇。。。
#p1denom   侮辱性文档中侮辱性词汇总数（会重复）
#p0denom
#pabusive  侮辱性文档占总文档数占比
def trainNB0(trainMatrix,trainCategory):   #trainMatrix:二维，维数是文章数，长度是总词汇数。每篇文章单词在总词汇集合中有无，无0有1  #trainCategory：[0,1,0,1,0,1]0表示非侮辱文章，1表示侮辱。列表长度代表文章数
    numTrainDocs=len(trainMatrix)  #总篇数
    #print("trainmatrix:",trainMatrix)
    numWords=len(trainMatrix[0])   #文章单词数
    pAbusive=sum(trainCategory)/float(numTrainDocs)  #侮辱性文章占总文章占比
    p0Num=np.ones(numWords)
    p1Num=np.ones(numWords)
    p1Vect=np.zeros(numWords)
    p0Vect=np.zeros(numWords)
    p0Denom=2.0
    p1Denom=2.0
    for i in range(numTrainDocs):   #扫描文档侮辱性or非侮辱
        if trainCategory[i]==1:    #是侮辱
            p1Num+=trainMatrix[i]   #将文章中词汇在侮辱性词汇列表中对应+1
            p1Denom+=sum(trainMatrix[i])   #总词汇:加文章总单词数
        else:
            p0Num+=trainMatrix[i]
            p0Denom+=sum(trainMatrix[i])
    #P(wn|c)
    for i in range(0,numWords):
        p1Vect[i]=math.log(p1Num[i]/p1Denom)
        p0Vect[i]=math.log(p0Num[i]/p0Denom)
    return p0Vect,p1Vect,pAbusive
def classifyNB(vec2Classify,p0Vec,p1Vec,pClass1):
    p1=sum(vec2Classify*p1Vec)+math.log(pClass1)   #p(w1,w2,w3..|c1)*p(c1)=p(w1|c1)*p(w2|c2)*...p(c1)   (log模式相加)
    p0=sum(vec2Classify*p0Vec)+math.log(1-pClass1)
    #没有除p(w)(所测文章内单词占总单词比例),两者p(w)相同======p1\p0相当于p(c1|w)   p(c0|w)
    if p1>p0:
        return 1   #
    else:
        return 0
def testingNB():
    listOposts,listClasses=loadDataSet()
    myVocalbList=createCabList(listOposts)    #不重复单词集合
    trainMat=[]
    for postinDoc in listOposts:
        trainMat.append(setOfWodrs2Vec(myVocalbList,postinDoc))
    p0V,p1V,pAb=trainNB0(np.array(trainMat),np.array(listClasses))
    testEntry=['love','my','dalmation']
    thisDoc=np.array(setOfWodrs2Vec(myVocalbList,testEntry))   #wn
    print(testEntry,"classified as:",classifyNB(thisDoc,p0V,p1V,pAb))
    testEntry=['stupid','garbage']
    thisDoc=np.array(setOfWodrs2Vec(myVocalbList,testEntry))   #wn
    print(testEntry,"classified as:",classifyNB(thisDoc,p0V,p1V,pAb))
def textParse(bigString):   #把邮件内容分割成单词并全部首字母小写
    import re  #正则化
    listOfTokens=re.split(r'\W*',  bigString)
    return [tok.lower() for tok in listOfTokens if len(tok)>2]  #首字母小写
def spamTest():
    docList=[]
    classList=[]
    fullText=[]
    for i in range(1,26):
        wordList=textParse(open('email/spam/%d.txt' %i).read())   #加载邮件
        docList.append(wordList)   #所有文章列表，单词
        fullText.extend(wordList)  #
        classList.append(1)         #所有文章列表，判断侮辱or非侮辱
        wordList=textParse(open('email/ham/%d.txt' % i).read())
        docList.append(wordList)   #每篇邮件单词汇总
        fullText.extend(wordList)   #
        classList.append(0)       #垃圾邮件
    vocabList=createCabList(docList)
    trainingSet=list(range(50))
    testSet=[]
    for i in range(10):
        randIndex=int(random.uniform(0,len(trainingSet)))
        testSet.append(trainingSet[randIndex])
        del(trainingSet[randIndex])
    trainMat=[]
    trainClasses=[]
    for docIndex in trainingSet:
        trainMat.append(setOfWodrs2Vec(vocabList,docList[docIndex]))
        trainClasses.append(classList[docIndex])

    p0V,p1V,pSpam=trainNB0(np.array(trainMat),np.array(trainClasses))  #p(w|c0)  p(w|c1)  p(c1)
    errorCount=0
    for docIndex in testSet:
        wordVextor=setOfWodrs2Vec(vocabList,docList[docIndex])
        if classifyNB(np.array(wordVextor),p0V,p1V,pSpam)!=classList[docIndex]:  #p(c|w)  判断训练误差
            errorCount+=1
    print("thr error rate is:",float(errorCount/len(testSet)))


spamTest()

  贝叶斯应用很广。玻尔认为：在人工智能中贝叶斯的问题在其只能应用在关联阶段。玻尔将人工智能分为三个阶段：关联、干预、反事实。若想从第一阶段跨越到第二阶段，需要利用因果关系( 源自《THE BOOK OF WHY》)