1.1 广义线性模型
1.1.1 普通最小二乘法
最小二乘法很经常用在线性回归Linear Regression, y^=Xw+b y ^ = X w + b 中,LR是用来拟合一个
J(w,b)=12m∑mi=1(y^(i)−y(i))2 J ( w , b ) = 1 2 m ∑ i = 1 m ( y ^ ( i ) − y ( i ) ) 2
然后再在梯度下降法Gradient Descent Optimization对系数w进行优化:
∂J∂wj=1m∑mi=1(y^(i)−y(i))x(i)j
∂
J
∂
w
j
=
1
m
∑
i
=
1
m
(
y
^
(
i
)
−
y
(
i
)
)
x
j
(
i
)
∂J∂b=1m∑mi=1(y^(i)−y(i))
∂
J
∂
b
=
1
m
∑
i
=
1
m
(
y
^
(
i
)
−
y
(
i
)
)
说明:
y^(i)表示第i个样本的预测值
y
^
(
i
)
表
示
第
i
个
样
本
的
预
测
值
y(i)表示第i个样本的真实值
y
(
i
)
表
示
第
i
个
样
本
的
真
实
值
x(i)j
x
j
(
i
)
指的是第i个样本的第j个特征的值。
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score # 模型评价指标
import matplotlib.pyplot as plt
import numpy as np
# 生成500个点数据
X = 2 * np.random.rand(500, 1)
y = 5 + 3 * X + np.random.randn(500, 1)
plt.scatter(X, y)
plt.title("Dataset")
plt.xlabel('X')
plt.ylabel('y')
plt.show()# 下面使用Sklearn中的线性回归模型进行拟合
lr = LinearRegression()
lr.fit(X, y)
# 再使用这个模型进行数据的预测
y_pred = lr.predict(X)
# 输出这个模型拟合的系数
print('The cofficients of lr is : ', lr.coef_)
# 计算mean squared error
print('The mse of the training sets is : ', mean_squared_error(y_true=y, y_pred=y_pred))
# 将模型拟合的图画出来
plt.scatter(X ,y, color='orange')
plt.plot(X, y_pred, color='red', linewidth=1) # 拟合直线
plt.xticks([])
plt.yticks([])
plt.show()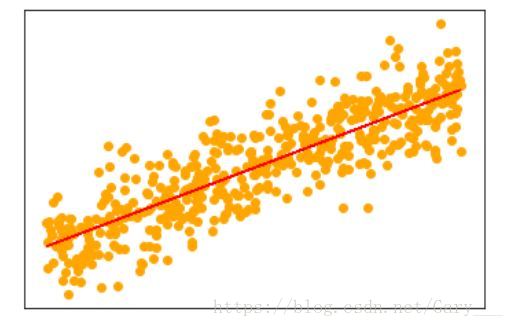
由图可知,拟合的直线正好符合散点图的趋向
1.1.2 岭回归Ridge Regression
岭回归是线性回归的一个改善的版本,对系数施加L2正则:
其中α>=0, 是控制系数的收缩量的发杂性参数,α值越大,收缩量也就越大。
梯度下降在Ridge上的运用就不再做详细的推导,同学们可以按照上面的Linear Regression的推导进行练习,不难的。
from sklearn.linear_model import Ridge
## 引用上面的数据
ridge = Ridge(alpha=0.5)
ridge.fit(X, y)
# 再使用这个模型进行数据的预测
y_pred = ridge.predict(X)
# 输出这个模型拟合的系数
print('The cofficients of lr is : ', ridge.coef_)
# 计算mean squared error
print('The mse of the training sets is : ', mean_squared_error(y_true=y, y_pred=y_pred))
# 将模型拟合的图画出来
plt.scatter(X ,y, color='orange')
plt.plot(X, y_pred, color='red', linewidth=1) # 拟合直线
plt.xticks([])
plt.yticks([])
plt.show()在小型的数据集上,可能与无正则项的Linear Regression相差不大,但是加入正则项是可以是模型更加的鲁棒。
添加Cross Validation找出更加优秀的alpha系数。
# 我们还可以为岭回归添加交叉性验证
from sklearn.linear_model import RidgeCV
rid_cv = RidgeCV() # alpha=(0.1, 1.0, 10.0) # 通过cv找到更好的alpha系数
rid_cv.fit(X, y)
# 再使用这个模型进行数据的预测
y_pred = rid_cv.predict(X)
# 输出这个模型拟合的系数
print('The cofficients of lr is : ', rid_cv.coef_)
# 计算mean squared error
print('The mse of the training sets is : ', mean_squared_error(y_true=y, y_pred=y_pred))1.1.3 Lasso
Lasso也是线性回归的一个改善模型,不过这个是加入了L1正则项,以获得稀疏解:
from sklearn.linear_model import Lasso
reg = Lasso(alpha=0.1)
reg.fit(X, y)
# 再使用这个模型进行数据的预测
y_pred = reg.predict(X)
# 输出这个模型拟合的系数
print('The cofficients of lr is : ', reg.coef_)
# 计算mean squared error
print('The mse of the training sets is : ', mean_squared_error(y_true=y, y_pred=y_pred))本人github,欢迎star/follow:https://github.com/Gary-Deeplearning/sklearn-study-note






 本文详细介绍了线性模型的各种形式,包括普通最小二乘法、岭回归、Lasso等,并通过Python代码实例展示了如何使用这些模型进行数据拟合。
本文详细介绍了线性模型的各种形式,包括普通最小二乘法、岭回归、Lasso等,并通过Python代码实例展示了如何使用这些模型进行数据拟合。
















 845
845

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








