——————————————————以下为正文——————————————————
从线性空间的角度看，在一个定义了内积的线性空间里，对一个N阶 对称方阵进行特征分解，就是产生了该空间的N个标准正交基，然后把矩阵投影到这N个基上。N个特征向量就是N个标准正交基，而特征值的模则代表矩阵在每个基上的投影长度。
特征值越大，说明矩阵在对应的特征向量上的方差越大，功率越大，信息量越多。
应用到最优化中，意思就是对于R的二次型，自变量在这个方向上变化的时候，对函数值的影响最大，也就是该方向上的方向导数最大。
应用到数据挖掘中，意思就是最大特征值对应的特征向量方向上包含最多的信息量，如果某几个特征值很小，说明这几个方向信息量很小，可以用来降维，也就是删除小特征值对应方向的数据，只保留大特征值方向对应的数据，这样做以后数据量减小，但有用信息量变化不大。
——————————————————举两个栗子——————————————————
应用1 二次型最优化问题
二次型
，其中R是已知的二阶矩阵，R=[1，0.5；0.5，1]，x是二维列向量，x=[x1；x2]，求y的最小值。
求解很简单，讲一下这个问题与特征值的关系。
对R特征分解，特征向量是[-0.7071；0.7071]和[0.7071；0.7071]，对应的特征值分别是0.5和1.5。
然后把y的等高线图画一下
从图中看，函数值变化最快的方向，也就是曲面最陡峭的方向，归一化以后是[0.7071；0.7071]，嗯哼，这恰好是矩阵R的一个特征值，而且它对应的特征向量是最大的。因为这个问题是二阶的，只有两个特征向量，所以另一个特征向量方向就是曲面最平滑的方向。这一点在分析最优化算法收敛性能的时候需要用到。
从图中看，函数值变化最快的方向，也就是曲面最陡峭的方向，归一化以后是[0.7071；0.7071]，嗯哼，这恰好是矩阵R的一个特征值，而且它对应的特征向量是最大的。因为这个问题是二阶的，只有两个特征向量，所以另一个特征向量方向就是曲面最平滑的方向。这一点在分析最优化算法收敛性能的时候需要用到。
二阶问题比较直观，当R阶数升高时，也是一样的道理。
应用2 数据降维
兴趣不大的可以跳过问题，直接看后面降维方法。
机器学习中的分类问题，给出178个葡萄酒样本，每个样本含有13个参数，比如酒精度、酸度、镁含量等，这些样本属于3个不同种类的葡萄酒。任务是提取3种葡萄酒的特征，以便下一次给出一个新的葡萄酒样本的时候，能根据已有数据判断出新样本是哪一种葡萄酒。
问题详细描述： UCI Machine Learning Repository: Wine Data Set
训练样本数据： http://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data
原数据有13维，但这之中含有冗余，减少数据量最直接的方法就是降维。
做法：把数据集赋给一个178行13列的矩阵R，它的协方差矩阵
，C是13行13列的矩阵，对C进行特征分解，对角化
，其中U是特征向量组成的矩阵，D是特征之组成的对角矩阵，并按由大到小排列。然后，另
，就实现了数据集在特征向量这组正交基上的投影。嗯，重点来了，R’中的数据列是按照对应特征值的大小排列的，后面的列对应小特征值，去掉以后对整个数据集的影响比较小。比如，现在我们直接去掉后面的7列，只保留前6列，就完成了降维。这个降维方法叫PCA（Principal Component Analysis）。
下面看结果：
这是不降维时候的分类错误率。
这是不降维时候的分类错误率。
这是降维以后的分类错误率。
结论：降维以后分类错误率与不降维的方法相差无几，但需要处理的数据量减小了一半（不降维需要处理13维，降维后只需要处理6维）。
特征值不仅仅是数学上的一个定义或是工具，特征值是有具体含义的，是完全看得见摸得着的。
1. 比如说一个三维矩阵，理解成线性变换，作用在一个球体上：
三个特征值决定了 对球体在三个维度上的拉伸/压缩，把球体塑造成一个橄榄球；
剩下的部分决定了这个橄榄球在三维空间里面怎么旋转。
2. 对于一个微分方程：
将系数提取出来
对角化：
其中
由于
定义
于是有
因此y的变化率与特征值息息相关：
再将y由Q变换回x，我们就能得出x在不同时间的值。x的增长速度就是特征值λ，Q用来把x旋转成y。
-----------------------------------------
详细信息参看《神奇的矩阵》
----这是打广告的分割线---------
想要理解特征值，首先要理解矩阵相似。什么是矩阵相似呢？从定义角度就是：存在可逆矩阵P满足B＝
则我们说A和B是相似的。让我们来回顾一下之前得出的重要结论：对于同一个线性空间，可以用两组不同的基
![[\alpha ]](https://i-blog.csdnimg.cn/blog_migrate/d34ef1487e86eff5edfb941978aa325d.png)
和基
![[\beta ]](https://i-blog.csdnimg.cn/blog_migrate/6c32ce9b013a566e1b537b107f270ef1.png)
来描述，他们之间的过渡关系是这样的：
![[\beta ]=[\alpha ]P](https://i-blog.csdnimg.cn/blog_migrate/6c32ce9b013a566e1b537b107f270ef1.png%3D%5B%5Calpha+%5DP)
，而对应坐标之间的过渡关系是这样的：
我们知道，对于一个线性变换，只要你选定一组基，那么就可以用一个矩阵T1来描述这个线性变换。换一组基，就得到另一个不同的矩阵T2（之所以会不同，是因为选定了不同的基，也就是选定了不同的坐标系）。所有这些矩阵都是这同一个线性变换的描述，但又都不是线性变换本身。具体来说，有一个线性变换，我们选择基
来描述，对应矩阵是T1；同样的道理，我们选择基来描述，，对应矩阵是T2；我们知道基
和基是有联系的，那么他们之间的变换T1和T2有没有联系呢？
当然有，T1和T2就是相似的关系，具体的请看下图：
没错，所谓相似矩阵，就是同一个线性变换的不同基的描述矩阵。这就是相似变换的几何意义。
这个发现太重要了。原来一族相似矩阵都是同一个线性变换的描述啊！难怪这么重要！工科研究生课程中有矩阵论、矩阵分析等课程，其中讲了各种各样的相似变换，比如什么相似标准型，对角化之类的内容，都要求变换以后得到的那个矩阵与先前的那个矩阵式相似的，为什么这么要求？因为只有这样要求，才能保证变换前后的两个矩阵是描述同一个线性变换的。就像信号处理（积分变换）中将信号（函数）进行拉氏变换，在复数域处理完了之后又进行拉式反变换，回到实数域一样。信号处理中是主要是为了将复杂的卷积运算变成乘法运算。其实这样的变换还有好多，有兴趣可以看积分变换的教材。
为什么这样做呢？矩阵的相似变换可以把一个比较丑的矩阵变成一个比较美的矩阵，而保证这两个矩阵都是描述了同一个线性变换。至于什么样的矩阵是“美”的，什么样的是“丑”的，我们说对角阵是美的。在线性代数中，我们会看到，如果把复杂的矩阵变换成对角矩阵，作用完了之后再变换回来，这种转换很有用处，比如求解矩阵的n次幂！而学了矩阵论之后你会发现，矩阵的n次幂是工程中非常常见的运算。这里顺便说一句，将矩阵对角化在控制工程和机械振动领域具有将复杂方程解耦的妙用！ 总而言之，相似变换是为了简化计算！
从另一个角度理解矩阵就是：矩阵主对角线上的元素表示自身和自身的关系，其他位置的元素aij表示i位置和j位置元素之间的相互关系。那么好，特征值问题其实就是选取了一组很好的基，就把矩阵 i位置和j位置元素之间的相互关系消除了。而且因为是相似变换，并没有改变矩阵本身的特性。因此矩阵对角化才如此的重要！
特征向量的引入是为了选取一组很好的基。空间中因为有了矩阵，才有了坐标的优劣。对角化的过程，实质上就是找特征向量的过程。如果一个矩阵在复数域不能对角化，我们还有办法把它化成比较优美的形式——Jordan标准型。高等代数理论已经证明：一个方阵在复数域一定可以化成Jordan标准型。这一点有兴趣的同学可以看一下高等代数后或者矩阵论。
特征值英文名eigen value。“特征”一词译自德语的eigen，由希尔伯特在1904年首先在这个意义下使用（赫尔曼·冯·亥姆霍兹在更早的时候也在类似意义下使用过这一概念）。eigen一词可翻译为“自身的”，“特定于...的”，“有特征的”或者“个体的”—这强调了特征值对于定义特定的变换上是很重要的。它还有好多名字，比如谱，本征值。为什么会有这么多名字呢？
原因就在于他们应用的领域不同，中国人为了区分，给特不同的名字。你看英文文献就会发现，他们的名字都是同一个。当然，特征值的思想不仅仅局限于线性代数，它还延伸到其他领域。在数学物理方程的研究领域，我们就把特征值称为本征值。如在求解薛定谔波动方程时，在波函数满足单值、有限、连续性和归一化条件下，势场中运动粒子的总能量(正)所必须取的特定值，这些值就是正的本征值。
前面我们讨论特征值问题面对的都是有限维度的特征向量，下面我们来看看特征值对应的特征向量都是无限维函数的例子。这时候的特征向量我们称为特征函数，或者本证函数。这还要从你熟悉的微分方程说起。方程本质是一种约束，微分方程就是在世界上各种各样的函数中，约束出一类函数。对于一阶微分方程
我们发现如果我将变量y用括号[]包围起来，微分运算的结构和线性代数中特征值特征向量的结构,即和
竟是如此相似。这就是一个求解特征向量的问题啊！只不过“特征向量”变成函数！我们知道只有
满足这个式子。这里出现了神奇的数e，一杯开水放在室内，它温度的下降是指数形式的；听说过放射性元素的原子核发生衰变么？随着放射的不断进行，放射强度将按指数曲线下降；化学反应的进程也可以用指数函数描述……类似的现象还有好多。
为什么选择指数函数而不选择其他函数，因为指数函数是特征函数。为什么指数函数是特征？我们从线性代数的特征向量的角度来解释。这已经很明显了就是“特征向量”。于是，很自然的将线性代数的理论应用到线性微分方程中。那么指数函数就是微分方程（实际物理系统）的特征向量。用特征向量作为基表示的矩阵最为简洁。就像你把一个方阵经过相似对角化变换，耦合的矩阵就变成不耦合的对角阵一样。在机械振动里面所说的模态空间也是同样的道理。如果你恰巧学过振动分析一类的课程，也可以来和我交流。
同理，用特征函数解的方程也是最简洁的，不信你用级数的方法解方程，你会发现方程的解有无穷多项。解一些其他方程的时候(比如贝塞尔方程)我们目前没有找到特征函数，于是退而求其次才选择级数求解，至少级数具有完备性。实数的特征值代表能量的耗散或者扩散，比如空间中热量的传导、化学反应的扩散、放射性元素的衰变等。虚数的特征值(对应三角函数)代表能量的无损耗交换，比如空间中的电磁波传递、振动信号的动能势能等。复数的特征值代表既有交换又有耗散的过程，实际过程一般都是这样的。复特征值在电路领域以及振动领域将发挥重要的作用，可以说，没有复数，就没有现代的电气化时代！
对于二阶微分方程方程，它的解都是指数形式或者复指数形式。可以通过欧拉公式将其写成三角函数的形式。复特征值体现最多的地方是在二阶系统，别小看这个方程，整本自动控制原理都在讲它，整个振动分析课程也在讲它、还有好多课程的基础都是以这个微分方程为基础，这里我就不详细说了，有兴趣可以学习先关课程。说了这么多只是想向你传达一个思想，就是复指数函数式系统的特征向量！
如果将二阶微分方程转化成状态空间
的形式(具体转化方法见现代控制理论，很简单的)
。则一个二阶线性微分方程就变成一个微分方程组的形式这时就出现了矩阵A，矩阵可以用来描述一个系统：如果是振动问题，矩阵A的特征值是虚数，对应系统的固有频率，也就是我们常说的，特征值代表振动的谱。如果含有耗散过程，特征值是负实数，对应指数衰减；特征值是正实数，对应指数发散过程，这时是不稳定的，说明系统极容易崩溃，如何抑制这种发散就是控制科学研究的内容。
提到振动的谱，突然想到了这个经典的例子：美国数学家斯特让（G..Strang）在其经典教材《线性代数及其应用》中这样介绍了特征值作为频率的物理意义，他说："大概最简单的例子（我从不相信其真实性，虽然据说1831年有一桥梁毁于此因）是一对士兵通过桥梁的例子。传统上，他们要停止齐步前进而要散步通过。这个理由是因为他们可能以等于桥的特征值之一的频率齐步行进，从而将发生共振。就像孩子的秋千那样，你一旦注意到一个秋千的频率，和此频率相配，你就使频率荡得更高。一个工程师总是试图使他的桥梁或他的火箭的自然频率远离风的频率或液体燃料的频率；而在另一种极端情况，一个证券经纪人则尽毕生精力于努力到达市场的自然频率线。特征值是几乎任何一个动力系统的最重要的特征。"
对于一个线性系统，总可以把高阶的方程转化成一个方程组描述，这被称为状态空间描述。因此，他们之间是等价的。特征值还有好多用处，原因不在特征值本身，而在于特征值问题和你的物理现象有着某种一致的对应关系。学习特征值问题告诉你一种解决问题的方法：寻找事物的特征，然后特征分解。
-----------
我举一个直观一点的例子吧...我也喜欢数学的直观之美。
我们知道，一张图像的像素（如:320 x 320）到了计算机里面事实上就是320x320的矩阵，每一个元素都代表这个像素点的颜色..
如果我们把基于特征值的应用，如PCA、向量奇异值分解SVD这种东西放到图像处理上，大概就可以提供一个看得到的、直观的感受。关于SVD的文章可以参考LeftNotEasy的文章： 机器学习中的数学(5)-强大的矩阵奇异值分解(SVD)及其应用
简单的说，SVD的效果就是..用一个规模更小的矩阵去近似原矩阵...
这里A就是代表图像的原矩阵..其中的
尤其值得关注，它是由A的特征值
从大到小放到对角线上的..也就是说，我们可以选择其中的某些具有“代表性”的特征值去近似原矩阵！
左边的是原始图片
当我把特征值的数量减少几个的时候...后面的图像变“模糊”了..
当我把特征值的数量减少几个的时候...后面的图像变“模糊”了..
同样地...
同样地...
关键的地方来了！如果我们只看到这里的模糊..而没有看到计算机（或者说数学）对于人脸的描述，那就太可惜了...我们看到，不论如何模糊，脸部的关键部位（我们人类认为的关键部位）——五官并没有变化太多...这能否说：数学揭示了世界的奥秘？
看作一个线性变换，那么这个定义式就表示对于 向量
而言，经过
变换之后该向量的方向没有变化（可能会反向），而只是长度变化了（乘以
）。
也就是对于变换
来说，存在一些“不变”的量（比如特征向量
的方向），
我想，“特征”的含义就是“不变”。
而特征值
，如你所见，就是变换
在特征方向上的伸展系数吧（乱诹了个名词 :P）。
嗯，觉得维基其实讲的就挺好的： https://zh.wikipedia.org/wiki/%E7%89%B9%E5%BE%81%E5%90%91%E9%87%8F
特征值和特征向量是为了研究矩阵仿射变换的不变性而提出的，一个空间里的元素通过线性变换到另一个相同维数的空间，那么会有某些向量的方向在变换前后不会改变，方向不变但是这些向量的范数可能会改变，我这里说的都是实数空间的向量。
定义
，定义
为原始空间中的向量，
为变换后空间的向量，简单起见令
为
阶方阵且特征值
那么在变换到另一个空间时
好，下面再说更深层次的含义。
在不同的领域特征值的大小与特征向量的方向所表示的含义也不同，但是从数学定义上来看，每一个原始空间中的向量都要变换到新空间中，所以他们之间的差异也会随之变化，但是为了保持相对位置，每个方向变换的幅度要随着向量的分散程度进行调整。
你们体会一下拖拽图片使之放大缩小的感觉。
如果A为样本的协方差矩阵，特征值的大小就反映了变换后在特征向量方向上变换的幅度，幅度越大，说明这个方向上的元素差异也越大，换句话说这个方向上的元素更分散。
用特征向量作为基，线性变换会很简单，仅仅是伸缩变换，而特征值就是伸缩的大小。
各位已经说的很清楚了，我就发几张用mathematica做的图吧。
这里只给出一些“可视化”的2D线性变换。
在
平面当中的一个向量
经过一个线性变换（乘上一个矩阵）之后变成了另一个
的向量
，把它的起点接在
，就可以表示线性变换的特性。再画出一组特征向量，我们就有下图：
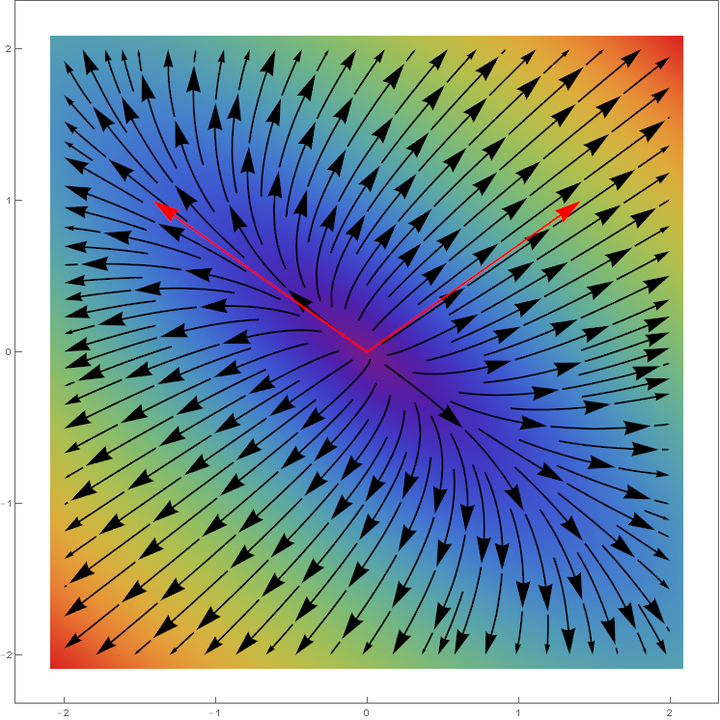
颜色越深冷，代表向量长度越小。
可以看出特征向量所在的直线上的向量经过变换之后方向不变，这意味着一个向量的分量是各自独立的，这对于我们分析矩阵、线性变换就方便了很多。
（绿色箭头是矩阵的行向量，红色是特征向量）
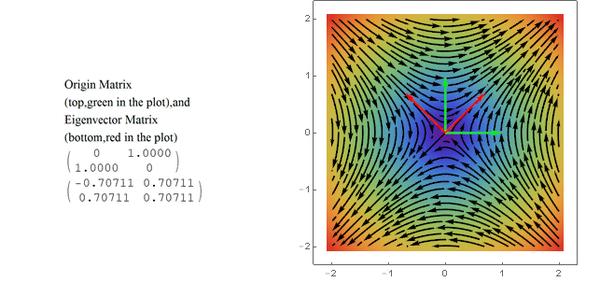
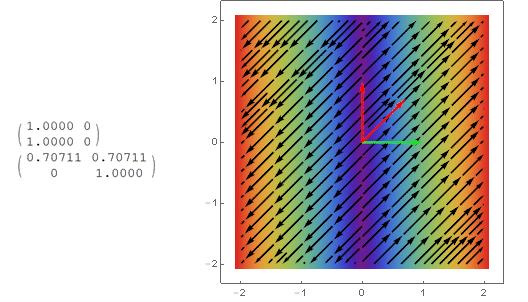
只有一个特征值-1的情况：
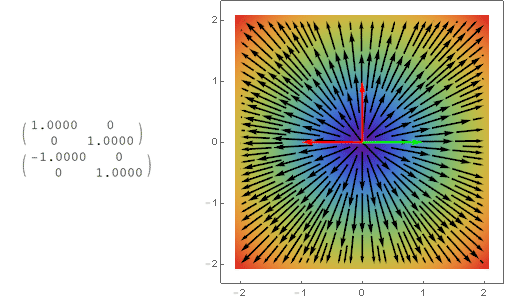
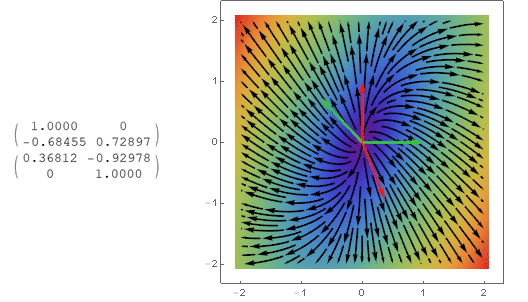
特征值是虚数的反对称矩阵：
其实做的是动图，可惜知乎不支持动图。
其实做的是动图，可惜知乎不支持动图。
为例，设它的3个特征值（多重特征值就重复写）分别为
,
和
，则
线性无关。
可表示为
,则有
扫一扫
2962
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
