从线性回归看偏差-方差分解（Bias-Variance Decomposition）

转载请注明出处：http://blog.youkuaiyun.com/gamer_gyt
博主微博：http://weibo.com/234654758
Github：https://github.com/thinkgamer
公众号：搜索与推荐Wiki

个人网站：http://thinkgamer.github.io

---

概述

对于数字序列1，3，5，7，？，正常情况下大家脑海里蹦出的是9，但是217314也是其一个解
9对应的数学公式为
$$f(x)=2x-1$$
217314对应的数学公式为
$$f(x)=\frac{18111}{2}{x}^4-90555x^3+\frac{633885}{2}{x}^2-452773x+217331$$
Python 实现为：

>>> def f(x):
...     return 18111/2 * pow(x,4) -90555 * pow(x,3) + 633885/2 * pow(x,2) -452773 * x +217331
... 
>>> f(1)
1.0
>>> f(2)
3.0
>>> f(3)
5.0
>>> f(4)
7.0
>>> f(5)
217341.0

当机器学习模型进行预测的时候，通常都需要把握一个非常微妙的平衡，一方面我们希望模型能够匹配更多的训练数据，相应的增加其复杂度，否则会丢失相关特征的趋势（即模型过拟合）；但是另一方面，我们又不想让模型过分的匹配训练数据，相应的舍弃部分复杂的，因为这样存在过度解析所有异常值和伪规律的风险，导致模型的泛化能力差（即模型欠拟合）。因此在模型的拟合能力和复杂度之前取得一个比较好的权衡，对于一个模型来讲十分重要。而偏差-方差分解（Bias-Variance Decomposition）就是用来指导和分析这种情况的工具。

偏差和方差定义

• 偏差（Bias）：即预测数据偏离真实数据的情况。
• 方差（Variance）：描述的是随机变量的离散程度，即随机变量在其期望值附近的波动程度。

偏差-方差推导过程

以回归问题为例，假设样本的真实分布为p_r(x,y)，并采用平方损失函数，模型f(x)的期望错误为(公式2.1)：
$$R(f)=E_{(x,y)\sim p_r(x,y)}\left[(y-f(x){)}^2\right]$$
那么最优模型为(公式2.2)：
$$f^{\ast }(x)=E_{y\sim p_r(y|x)}\left[y\right]$$
其中p_r(y|x)为真实的样本分布，f^*(x)为使用平方损失作为优化目标的最优模型，其损失为(公式2.3)：
$$\epsilon =E_{(x,y)\sim p_r(x,y)}\left[(y-f^{\ast }(x){)}^2\right]$$
损失
$$\epsilon$$
通常是由于样本分布及其噪声引起的，无法通过优化模型来减少。
期望错误可以分解为(公式2.4)：
$$R(f)$$
$$=E_{(x,y)\sim p_r(x,y)}\left[(y-f^{\ast }(x)+f^{\ast }(x)-f(x){)}^2\right]$$
$$=E_{x\sim p_r(x)}\left[(f(x)-f^{\ast }(x){)}^2\right]+\epsilon$$
公式2.4中的第一项是机器学习可以优化的真实目标，是当前模型和最优模型之间的差距。

在实际训练一个模型f(x)时，训练集D是从真实分布p_r(x,y)上独立同分布的采样出来的有限样本集合。不同的训练集会得到不同的模型。令f_D(x)表示在训练集D上学习到的模型，一个机器学习算法（包括模型和优化算法）的能力可以通过模型在不同训练集上的平均性能来体现。

对于单个样本x，不同训练集D得到的模型f_D(x)和最优模型f^*(x)的上的期望差距为（公式2.5）：
$$E_D[(f_D(x)-f^{\ast }(x){)}^2]$$
$$=E_D\left[(f_D(x)-E_D[f_D(x)]+E_D[f_D(x)]-f^{\ast }(x){)}^2\right]$$
$$=(E_D[f_D(x)]-f^{\ast }(x){)}^2)+E_D[(f_D(x)-E_D[f_D(x)]{)}^2]$$
公式2.5最后一行中的第一项为偏差(bias)，是指一个模型在不同训练集上的平均性能和与最优模型的差异，偏差可以用来衡量一个模型的拟合能力；第二项是方差（variance），是指一个模型在不同训练集上的差异，可以用来衡量一个模型是否容易过拟合。

集合公式2.4和公式2.5，期望错误可以分解为(公式2.6)：
$$R(f)=(bias{)}^2+variance+\epsilon$$
其中
$$(bias{)}^2=E_X[E_D[f_D(x)]-f^{\ast }(x){)}^2]$$
$$variance=E_X[E_D[(f_D(x)-E_D[f_D(x)]{)}^2]]$$
最小化期望错误等价于最小化偏差和方差之和。

偏差和方差分析

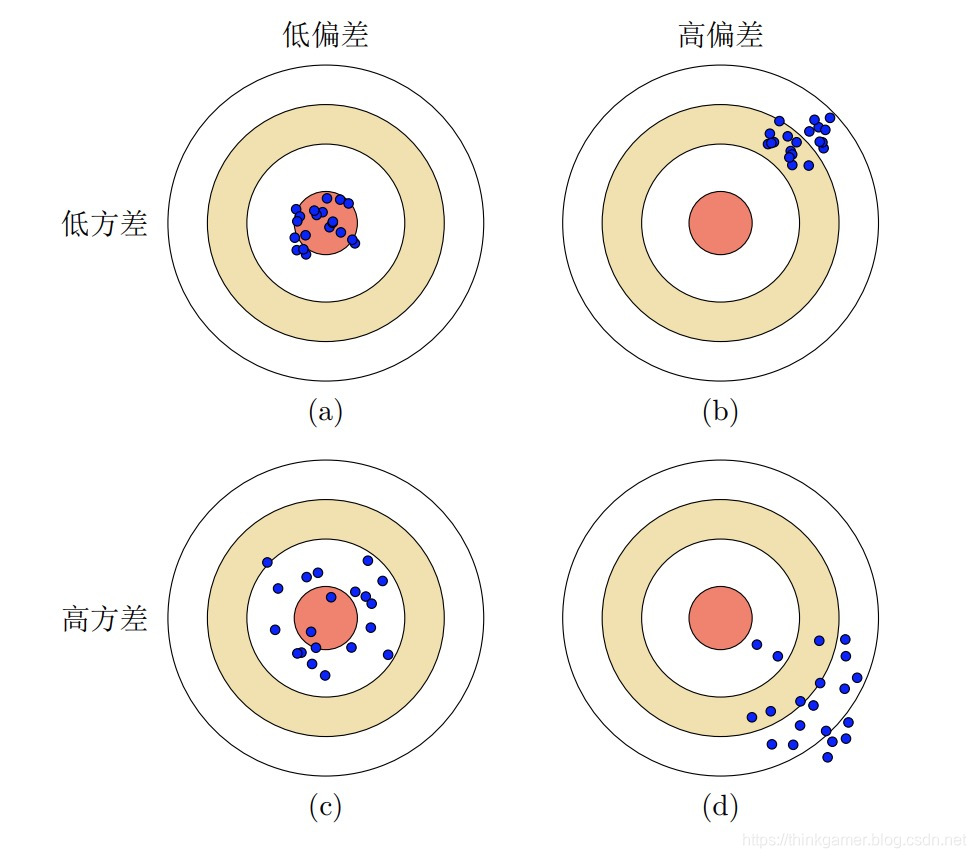
上图为机器学习中偏差和方差的四种不同情况。每个图的中心点为最优模型f*(x)，蓝点为不同训练集D 上得到的模型f_D(x)。

• (a)给出了一种理想情况，方差和偏差都比较小
• (b)为高偏差低方差的情况，表示模型的泛化能力很好，但拟合能力不足
• ©为低偏差高方差的情况，表示模型的拟合能力很好，但泛化能力比较差。当训练数据比较少时会导致过拟合
• (d)为高偏差高方差的情况，是一种最差的情况

方差一般会随着训练样本的增加而减少。当样本比较多时，方差比较少，我们可以选择能力强的模型来减少偏差。然而在很多机器学习任务上，训练集上往往都比较有限，最优的偏差和最优的方差就无法兼顾。

随着模型复杂度的增加，模型的拟合能力变强，偏差减少而方差增大，从而导致过拟合。以结构错误最小化为例，我们可以调整正则化系数λ来控制模型的复杂度。当λ变大时，模型复杂度会降低，可以有效地减少方差，避免过拟合，但偏差会上升。当λ过大时，总的期望错误反而会上升。因此，正则化系数λ需要在偏差和方差之间取得比较好的平衡。下图给出了机器学习模型的期望错误、偏差和方差随复杂度的变化情况。最优的模型并不一定是偏差曲线和方差曲线的交点。

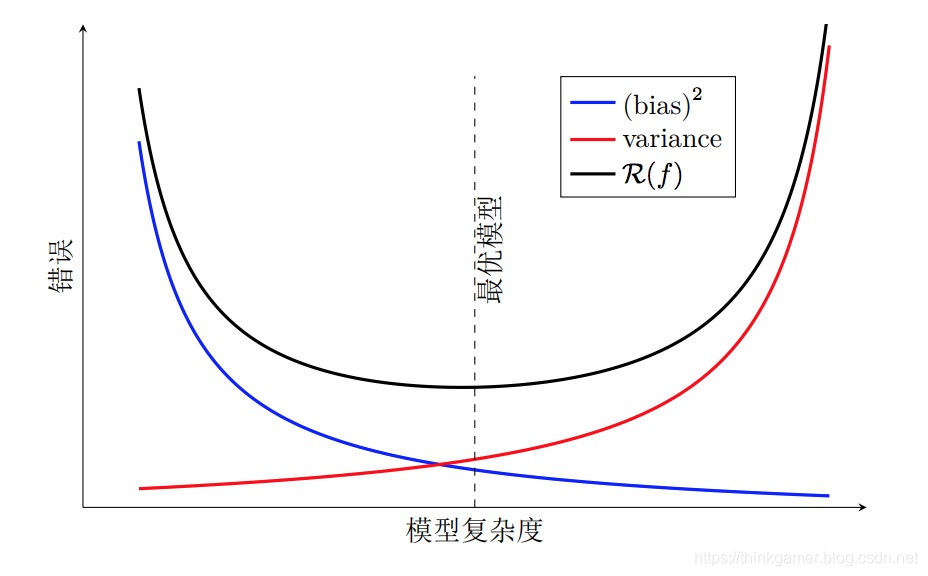
偏差和方差分解给机器学习模型提供了一种分析途径，但在实际操作中难以直接衡量。一般来说，当一个模型在训练集上的错误率比较高时，说明模型的拟合能力不够，偏差比较高。这种情况可以增加数据特征、提高模型复杂度，减少正则化系数等操作来改进模型。当模型在训练集上的错误率比较低，但验证集上的错误率比较高时，说明模型过拟合，方差比较高。这种情况可以通过降低模型复杂度，加大正则化系数，引入先验等方法来缓解。此外，还有一种有效的降低方差的方法为集成模型，即通过多个高方差模型的平均来降低方差。

---

【技术服务】，详情点击查看： https://mp.weixin.qq.com/s/PtX9ukKRBmazAWARprGIAg

---

扫一扫 关注微信公众号！号主 专注于搜索和推荐系统，尝试使用算法去更好的服务于用户，包括但不局限于机器学习，深度学习，强化学习，自然语言理解，知识图谱，还不定时分享技术，资料，思考等文章！

---