人工智能-机器学习（四）——逻辑回归_人工智能函数分类与回归-优快云博客

一、学习目标

基础认知：明确逻辑回归的核心定位（二分类模型）、典型应用场景，掌握 sigmoid 函数、概率基础等核心数学工具；
技能掌握：理解逻辑回归的建模思想（线性映射→概率转换→分类）、交叉熵损失函数的意义，熟练使用 sklearn 逻辑回归 API；
实战能力：独立完成数据预处理（缺失值、标准化）、模型训练与评估，通过癌症分类案例落地二分类任务。

二、目录

第一章逻辑回归简介（定位与应用）

1.1 逻辑回归的核心定位

1.2 典型应用场景

第二章逻辑回归的数学基础

2.1 sigmoid 激活函数（概率转换工具）

2.2 概率基础（边际 / 联合 / 条件概率）

第三章逻辑回归核心原理

3.1 建模基本思想

3.2 假设函数（线性→概率的桥梁）

3.3 交叉熵损失函数（模型优化目标）

3.4 似然函数与极大似然估计（优化逻辑来源）

3.5 交叉熵与似然函数的关系（优化目标统一）

第四章 API 详解与癌症分类实战

4.1 核心 API：sklearn.linear_model.LogisticRegression

4.2 实战案例：乳腺癌良恶性分类

4.3 结果分析与关键注意事项

第五章整体总结

第一章逻辑回归简介（定位与应用）

1.1 逻辑回归的核心定位

逻辑回归是解决二分类问题的经典模型，其本质是：

将线性回归的连续输出 $w^TX + b$ 通过 sigmoid 函数映射到（0,1）区间，转化为 “属于某一类的概率”，再通过阈值（如 0.5）实现分类。

⚠️ 注意：虽名为 “回归”，但实际是分类模型，仅用于二分类（多分类需扩展为 Softmax 回归）。

1.2 典型应用场景

逻辑回归因模型简单、可解释性强，广泛应用于需输出 “分类概率” 的二分类任务：

应用领域	具体场景	分类标签（0/1）
医疗健康	疾病诊断（如癌症、新冠）	0 = 阴性，1 = 阳性
金融风控	贷款风险评估	0 = 不放贷，1 = 放贷
自然语言处理	情感分析（如评论、舆情）	0 = 负面，1 = 正面
互联网营销	广告点击率预测（CTR）	0 = 不点击，1 = 点击
工业质检	产品缺陷检测	0 = 合格，1 = 不合格

思考：你还能想到哪些二分类场景？（如 “用户是否流失”“邮件是否为垃圾邮件” 等）

第二章逻辑回归的数学基础

2.1 sigmoid 激活函数（概率转换工具）

sigmoid 函数是逻辑回归的 “核心桥梁”，负责将线性模型的输出 $(-\infty, +\infty)$ 映射到（0,1）区间，输出值可解释为 “样本属于 1 类的概率”。

2.1.1 函数公式与图像

公式： $f(x) = \frac{1}{1 + e^{-x}}$
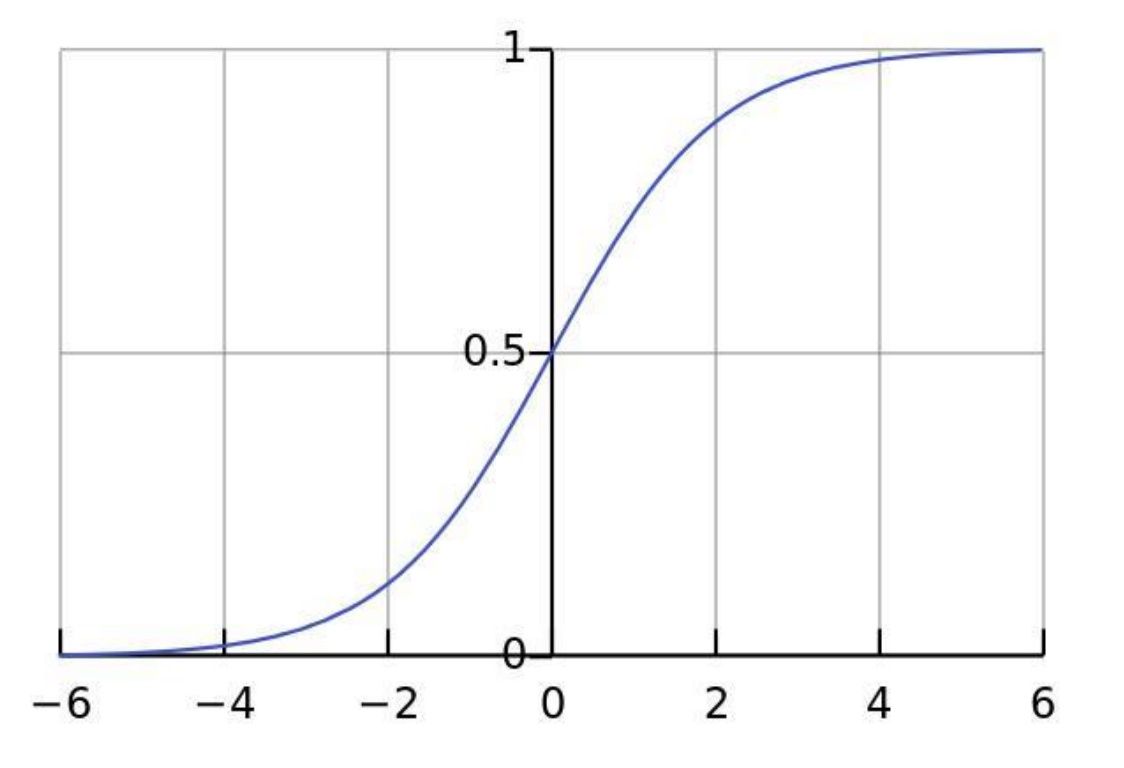
图像特征：S 型曲线，拐点在x=0处（此时f(0)=0.5），两端趋近于 0 或 1。

2.1.2 核心性质

取值范围：f(x) \in (0,1)，满足概率的取值要求；
单调性：单调递增（x越大，f(x)越接近 1，即属于 1 类的概率越高）；
导数特性： $f'(x) = f(x) \cdot (1 - f(x))$ （计算简便，大幅降低梯度下降的复杂度，是逻辑回归选择 sigmoid 的关键原因）。

2.1.3 分类逻辑

通过设定阈值（默认 0.5）判断类别：

若f(x) > 0.5：预测为 1 类（属于 1 类的概率更高）；
若f(x) < 0.5：预测为 0 类；
若f(x) = 0.5：可自定义规则（如随机分配或归为 1 类）。

2.2 概率基础（似然函数的前提）

逻辑回归的优化依赖 “概率最大化” 思想，需先理解三类基础概率：

概率类型	定义	表示符号	示例（疾病诊断）
边际概率	单一事件发生的概率	P(A)	P(患病)=0.3（整体患病概率）
联合概率	多个独立事件同时发生的概率	P(A \cap B)或P(A,B)	P(年龄>60, 患病)=0.2
条件概率	事件 A 已发生时，事件 B 发生的概率	P(B \mid A)	P(患病 \mid 年龄>60)=0.67

第三章逻辑回归核心原理

3.1 建模基本思想

逻辑回归的建模流程可概括为 “三步法”，核心是 “线性计算→概率转换→分类判断”：

第一步：线性计算：用线性模型（类似线性回归）计算特征的加权和：

$z = w^T X + b$ （w为权重向量，X为特征向量，b为偏置）；

第二步：概率转换：将z输入 sigmoid 函数，得到属于 1 类的概率：

$P(y=1 \mid X) = f(z) = \frac{1}{1 + e^{-(w^T X + b)}}$ ；

第三步：分类判断：根据概率与阈值的大小，输出最终类别（0 或 1）。

3.2 假设函数（模型的数学表达）

逻辑回归的假设函数（即预测函数）直接体现上述思想，分为 “概率形式” 和 “类别形式”：

概率形式（输出 1 类的概率）：

$h_w(X) = P(y=1 \mid X; w,b) = \frac{1}{1 + e^{-(w^T X + b)}}$ ；

类别形式（输出最终类别）：

$y_{pred} = \begin{cases} 1, & h_w(X) > 0.5 \\ 0, & h_w(X) < 0.5 \end{cases}$

⚠️ 说明：假设函数的参数是w（权重）和b（偏置），模型训练的目标就是找到最优w和b，使分类误差最小。

3.3 交叉熵损失函数（模型优化目标）

逻辑回归不能用线性回归的 MSE 损失函数（会导致损失函数非凸，存在多个局部极小值），需使用交叉熵损失函数（凸函数，仅一个全局极小值，便于优化）。

3.3.1 损失函数公式

对于单个样本 $(X, y)$ ， $y \in \{0,1\}$ ，交叉熵损失为：

$L(h_w(X), y) = -[y \cdot \log(h_w(X)) + (1 - y) \cdot \log(1 - h_w(X))]$ ；

对于m个样本，总损失（平均交叉熵）为：

$J(w,b) = -\frac{1}{m} \sum_{i=1}^m [y_i \cdot \log(h_w(X_i)) + (1 - y_i) \cdot \log(1 - h_w(X_i))]$ 。

3.3.2 损失函数的意义

当y=1（真实类别为 1）：损失简化为 $-\log(h_w(X))$ ，若 $h_w(X)$ 接近 1（预测准确），损失接近 0；若 $h_w(X)$ 接近 0（预测错误），损失趋近于 $+\infty$ ；
当y=0（真实类别为 0）：损失简化为 $-\log(1 - h_w(X))$ ，若 $h_w(X)$ 接近 0（预测准确），损失接近 0；若 $h_w(X)$ 接近 1（预测错误），损失趋近于 $+\infty$ 。

3.3.3 手工计算示例

假设 3 个样本的真实标签 $y=[1,0,1]$ ，预测概率 $h_w(X)=[0.4, 0.68, 0.41]$ ，则总损失为：

样本序号	真实标签 $ y_i $	预测为1的概率 $ \hat{p}_i $
1	1	0.8
2	0	0.3
3	1	0.6

单个样品计算：

1. 样本1： $y_1=1,\hat{p}_1=0.8$ ：

代入公式得： $L_1 = -[1 \cdot \ln(0.8) + (1-1) \cdot \ln(1-0.8)] = -\ln(0.8) \approx -(-0.2231) = 0.2231$

2. 样本2： $y_2=0,\hat{p}_2=0.3$ ：

代入公式得： $L_2 = -[0 \cdot \ln(0.3) + (1-0) \cdot \ln(1-0.3)] = -\ln(0.7) \approx -(-0.3567) = 0.3567$

3. 样本3： $y_3=1,\hat{p}_3=0.6$ ：

代入公式得： $L_3 = -[1 \cdot \ln(0.6) + (1-1) \cdot \ln(1-0.6)] = -\ln(0.6) \approx -(-0.5108) = 0.5108$

总损失计算：

将3个样本的损失相加，得到总损失：

$TotalLoss = 0.2231 + 0.3567 + 0.5108 = 1.0906$

3.4 似然函数与极大似然估计（优化逻辑来源）

逻辑回归的优化目标本质是 “最大化样本被正确分类的概率”，这一思想通过极大似然估计实现。

3.4.1 伯努利分布的似然函数

逻辑回归的输出服从伯努利分布（样本仅两种结果：0 或 1）。对于单个样本，正确分类的概率可统一表示为：

$P(y \mid X; w,b) = [h_w(X)]^y \cdot [1 - h_w(X)]^{1 - y}$ （y=1时为 $h_w(X)$ ，y=0时为 $1 - h_w(X)$ ）。

对于m个独立样本，似然函数（所有样本正确分类的联合概率）为：

$L(w,b) = \prod_{i=1}^m [h_w(X_i)]^{y_i} \cdot [1 - h_w(X_i)]^{1 - y_i}$ （连乘表示 “同时发生”）。

3.4.2 极大似然估计的思想

“极大似然估计” 即：找到参数w和b，使似然函数 $L(w,b)$ 最大（即 “已观测到的样本，其发生概率最大”）。

3.5 交叉熵与似然函数的关系（优化目标统一）

似然函数是 “连乘” 形式，计算复杂且易出现数值下溢，需通过以下两步转化为 “最小化交叉熵”：

取负对数：将 “最大化似然函数” 转化为 “最小化负对数似然函数”（对数是单调递增函数，不改变极值位置）：

$-\log L(w,b) = -\sum_{i=1}^m [y_i \cdot \log h_w(X_i) + (1 - y_i) \cdot \log(1 - h_w(X_i))]$ ；

除以样本数：得到 “平均负对数似然函数”，即交叉熵损失函数：

$J(w,b) = -\frac{1}{m} \log L(w,b)$ 。

结论：逻辑回归的 “最小化交叉熵损失” 等价于 “最大化似然函数”，两者是同一优化目标的不同表达。

第四章 API 详解与癌症分类实战

4.1 核心 API：sklearn.linear_model.LogisticRegression

sklearn 的LogisticRegression是实现逻辑回归的核心工具，支持二分类与多分类（需指定multi_class），常用参数与属性如下：

类型	名称 / 参数	说明
参数	fit_intercept	是否计算偏置b（默认 True，建议保留）
	solver	优化器（默认sag，大数据用sag/saga，小数据用liblinear）
	C	正则化强度（倒数，C越小正则化越强，默认 1.0，防止过拟合）
	max_iter	最大迭代次数（默认 100，收敛不足时可增大，如 200）
属性	coef_	权重向量w（shape=(n_features,)，反映各特征对分类的影响程度）
	intercept_	偏置b（标量）
方法	fit(X_train, y_train)	训练模型（学习w和b）
	predict(X_test)	预测测试集类别（输出 0/1）
	predict_proba(X_test)	预测测试集属于各类别的概率（输出 shape=(n_samples, 2)，两列分别为 0/1 类概率）
	score(X_test, y_test)	计算测试集准确率（正确分类样本数 / 总样本数）

4.2 实战案例：乳腺癌良恶性分类

4.2.1 数据描述

来源：乳腺癌数据集（sklearn 可加载，或本地 CSV 文件）；
规模：699 条样本，11 列数据；
内容：
1. 第 1 列：样本 ID（无意义，需剔除）；
2. 第 2-10 列：医学特征（如细胞大小、纹理、光滑度等，共 9 个特征）；
3. 第 11 列（Class）：标签（2 = 良性，4 = 恶性，需统一为 0/1 便于建模）；
缺失值：16 个缺失值，用 “?” 标记，需处理。

4.2.2 完整代码实现

# 1. 导入所需库

import pandas as pd

import numpy as np

from sklearn.model_selection import train_test_split

from sklearn.preprocessing import StandardScaler

from sklearn.linear_model import LogisticRegression

from sklearn.metrics import accuracy_score  # 也可直接用estimator.score()

# 2. 数据加载与预处理

def load_and_preprocess_data(file_path='./data/breast-cancer-wisconsin.csv'):

    # 2.1 加载数据

    data = pd.read_csv(file_path)

    print("数据基本信息：")

    print(data.info())  # 查看数据类型与缺失值

    

    # 2.2 缺失值处理（替换"?"为NaN，删除含缺失值的行）

    data = data.replace(to_replace="?", value=np.NaN)

    data = data.dropna()  # 删除缺失值样本（16个缺失值，不影响整体）

    print(f"\n处理后样本数：{len(data)}")

    

    # 2.3 标签统一（2→0良性，4→1恶性）

    data["Class"] = data["Class"].map({2: 0, 4: 1})

    

    # 2.4 划分特征（X）与目标值（y）（剔除ID列）

    X = data.iloc[:, 1:-1]  # 第2-10列（9个特征）

    y = data["Class"]        # 第11列（标签）

    print(f"\n特征矩阵形状：{X.shape}，目标值形状：{y.shape}")

    

    # 2.5 分割训练集与测试集（8:2，固定random_state确保结果可复现）

    X_train, X_test, y_train, y_test = train_test_split(

        X, y, test_size=0.2, random_state=22

    )

    

    # 2.6 特征标准化（逻辑回归对量纲敏感，需标准化消除影响）

    scaler = StandardScaler()

    X_train_scaled = scaler.fit_transform(X_train)  # 训练集：拟合+转换

    X_test_scaled = scaler.transform(X_test)        # 测试集：仅用训练集参数转换

    

    return X_train_scaled, X_test_scaled, y_train, y_test, scaler

# 3. 模型训练与评估

def train_and_evaluate_logistic_reg():

    # 加载预处理后的数据

    X_train, X_test, y_train, y_test, _ = load_and_preprocess_data()

    

    # 3.1 实例化模型（默认二分类，solver选liblinear适合小数据）

    estimator = LogisticRegression(

        solver='liblinear',  # 小数据集推荐，支持L1/L2正则

        max_iter=200,        # 确保收敛

        C=1.0                # 正则化强度（默认，可调整）

    )

    

    # 3.2 训练模型

    estimator.fit(X_train, y_train)

    

    # 3.3 模型参数查看（分析特征重要性）

    print(f"\n模型权重（9个特征）：{estimator.coef_}")

    print(f"模型偏置：{estimator.intercept_[0]:.4f}")

    

    # 3.4 模型评估

    # 3.4.1 预测类别与概率

    y_pred = estimator.predict(X_test)  # 预测类别（0/1）

    y_pred_proba = estimator.predict_proba(X_test)  # 预测概率（0类概率，1类概率）

    

    # 3.4.2 计算准确率

    accuracy = estimator.score(X_test, y_test)  # 等价于accuracy_score(y_test, y_pred)

    

    # 3.4.3 输出结果

    print(f"\n测试集预测类别（前10个）：{y_pred[:10]}")

    print(f"测试集预测概率（前10个，[0类概率, 1类概率]）：\n{y_pred_proba[:10].round(4)}")

    print(f"\n模型测试集准确率：{accuracy:.4f}")  # 通常可达95%以上

# 4. 执行实战

if __name__ == "__main__":

    train_and_evaluate_logistic_reg()

4.2.3 结果分析

准确率：正常情况下模型准确率可达 95% 以上，说明逻辑回归对该数据集的分类效果良好；
权重意义：coef_中正值越大的特征，对 “恶性肿瘤（1 类）” 的贡献越大；负值越大的特征，对 “良性肿瘤（0 类）” 的贡献越大；
标准化的重要性：若不标准化，量纲大的特征（如 “细胞大小”）会主导线性计算，导致模型偏向该特征，降低泛化能力。

第五章整体总结

核心定位：逻辑回归是二分类模型，通过 sigmoid 函数将线性输出转化为概率，本质是 “概率型分类器”；
数学核心：
- sigmoid 函数：实现 “连续值→概率” 的映射，导数特性简化优化；
- 交叉熵损失：凸函数，等价于 “最大化似然函数”，是模型的优化目标；

API 关键：LogisticRegression的solver（根据数据量选择）、C（正则化）、fit_intercept（偏置）需根据场景调整；
实战要点：
- 数据预处理：必须处理缺失值，建议标准化（逻辑回归对量纲敏感）；
- 标签处理：二分类标签需统一为 0/1（避免非 0/1 标签导致报错）；
- 评估指标：基础用准确率，不平衡数据需用精确率、召回率、F1-score（后续可扩展）。