二叉查找树

最新推荐文章于 2024-08-30 11:57:26 发布

原创最新推荐文章于 2024-08-30 11:57:26 发布 · 499 阅读

2 ·

CC 4.0 BY-SA版权

数据结构同时被 2 个专栏收录

20 篇文章

订阅专栏

经典数据结构

13 篇文章

订阅专栏

一、树的定义
定义一棵树一般用递归的方法。一棵树是一些节点的集合。
深度：任意节点的深度从根到该节点的唯一路径长
高度：任意节点的高度是从该节点到一片树叶的最长路径长

二、输的遍历

前序遍历首先检查当前根节点的值，然后递归的遍历左子树和右子树。
中序遍历首先遍历左子树，然后检查当前根节点的值，最后遍历右子树。
后序遍历首先遍历左右子树，然后检查当根前节点的值。

层次遍历逐层检查树的节点。

如下面一棵树：

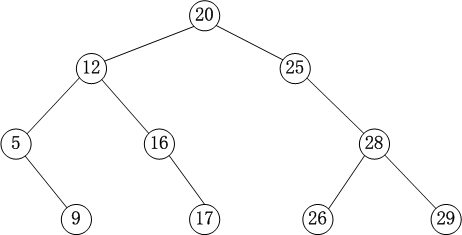
前序遍历：20 12 5 9 16 17 25 28 26 29

中序遍历：5 9 12 16 17 20 25 26 28 29

后序遍历：9 5 17 16 12 26 29 28 25 20

层次遍历：20 12 25 5 16 28 9 17 26 29

三、二叉查找树
二叉树(binary tree)是一棵树，其中每个节点都不能有多于两个的儿子。
平均二叉树的深度要比N小得多，二叉查找树(binary search tree)深度的平均值是O(logN)。
性质：对于树中的每个节点X，它的左子树中所有关键字值小于X的关键字值，而它的右子树中所有关键字值大于X的关键字值。

树的实现：由于树的递归定义，通常递归地编写树的操作。

四、二叉树的操作

1.插入操作
为了将X插入到树T中，可以像用Find那样沿着树查找。如果找到X，则什么也不做。否则，将X插入到遍历的路径上的最后一点上。

2.删除操作
如果节点是一片树叶，那么它可以被立即删除。如果节点有一个儿子，则该节点可以在其父节点调整指针绕过该节点后被删除。复杂的情况是处理具有两个儿子的节点。一般的删除策略是用其右子树的最小数据代替该节点的数据并递归地删除那个节点。因为右子树中的最小的节点不可能有左儿子，所以第二次删除要容易。

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<stack>
using namespace std;

typedef  struct  TreeNode{
        int  value;
        struct  TreeNode  *left;
        struct  TreeNode  *right;
}TreeNode;

TreeNode*  MakeEmpty(TreeNode* T);
TreeNode*  Find(TreeNode* T,int x);
TreeNode*  FindMin(TreeNode*);
TreeNode*  FindMax(TreeNode*);
TreeNode*  Insert(TreeNode*,int);
TreeNode*  Delete(TreeNode*,int);

TreeNode*
MakeEmpty(TreeNode* T)
{
        if (T != NULL)
        {
               MakeEmpty(T->left);
               MakeEmpty(T->right);
              free(T);
        }
        return NULL;
}

TreeNode* 
Find(TreeNode* T, int x)   //树查找一个元素
{
             if (T == NULL)
                      return NULL;
             if (x < T->value)
                      return Find(T->left, x);
             else if(x>T->value)
                      return Find(T->right,x);
             else
    return T;
}

TreeNode* 
FindMin(TreeNode* T)        //查找树的最小元素
{
         if (T == NULL)
                  return  NULL;
         else  if (T->left == NULL)
                  return  T;
         else
                  return  FindMin(T->left);
}

TreeNode* 
FindMax(TreeNode* T)             //查找树的最大元素
{
        if (T != NULL)
              while (T->right != NULL)
                          T = T->right;
        return T;
}

TreeNode*
Insert(TreeNode* T, int x)        //向树插入节点
{
           if (T == NULL)
           {
                      T = (TreeNode*)malloc(sizeof(TreeNode));
                      if (T == NULL)
                                printf("out of space!");
                      else {
                                   T->value = x;
                                   T->left = NULL;
                                   T->right = NULL;
                              }
           }
           if (x < T->value)
                      T->left = Insert(T->left, x);
           else  if (x > T->value)
                      T->right = Insert(T->right,x);
           return T;
}

TreeNode* 
Delete(TreeNode* T, int x)         //从树删除节点
{
          TreeNode *temp;
          if (T == NULL)
                   printf("x not found");
          else  if (x < T->value)
                   T->left = Delete(T->left, x);
          else  if (x > T->value)
                   T->right = Delete(T->right,x);
          else if (T->left && T->right)
          {
                   temp = FindMin(T->right);
                   T->value = temp->value;
                   T->right = Delete(T->right,T->value);
          }
          else
          {
                      temp = T;
                      if (T->left == NULL)
                                T = T->right;
                      else  if (T->right == NULL)
                                T = T->left;
                      free(temp);
           }
            return T;
}