二分法与循环不变性-优快云博客

本文链接：https://blog.youkuaiyun.com/GGGGGINALEX/article/details/131465301

文章探讨了二分查找算法的核心——循环中的不变性，详细解释了在不同区间形式下的二分法实现，并通过LeetCode的702二分查找和59螺旋矩阵II题目举例说明。在构建螺旋矩阵时，展示了如何利用循环不变性来简化问题，强调了理解并利用这一概念对于解决复杂编程问题的重要性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

二分法的核心是发现一次次循环中存在的不变性。

根据循环中区间的形式不变性，由此衍生出了二分的两种写法:

target 是在一个在左闭右闭的区间里，也就是[left, right]

	while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }

target 是在一个在左闭右开的区间里，也就是[left, right)

	while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }

参见 Leetcode - 702二分查找、Leetcode - 59 螺旋矩阵Ⅱ

在螺旋矩阵系列题目中，深切地体现了发现循环不变性的重要性。这系列题目显然是简单地模拟题，但是如果不能有效地确定好每次循环所要处理的区间，将一团乱麻。
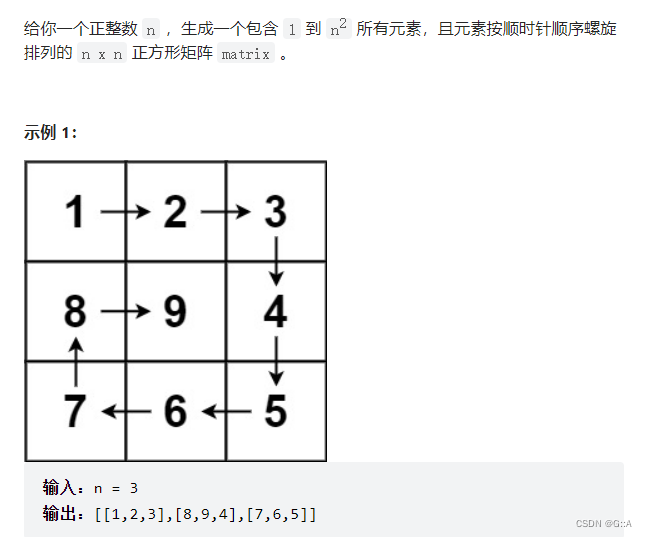
在这里插入图片描述

// 每次循环向四个方向走
        // n = 1;2 循环 1 次
        // n = 3;4 循环 2次
        int starti = 0; // 起点
        int startj = 0; // 起点
        int num = 0;
        for(int loop = 0; loop < (n)/2; loop ++) {
            int i = starti;
            int j = startj;
            // 向右走
            for(;j < n - loop - 1; j++) {
                ans[i][j] = ++num;
            }
            //向上走
            for(;i < n - loop - 1; i++) {
                ans[i][j] = ++num; 
            }
            for(;j >= startj + 1; j--) {
                ans[i][j] = ++num;
            }
            for(;i > starti; i--) {
                ans[i][j] = ++num;
            }
            starti ++;
            startj ++;