Java实现：挖金矿问题

挖金矿问题

• 使用递归的方式实现：

• public class text{
  
      /**
       * 获得金矿最优受益
       * @param: w   工人数量
       * @param: n   可选金矿数量
       * @param: p[] 金矿开采所需的工人数量
       * @param: g[] 金矿储量
       */
      public static void main(String[] args) {
  
          int w=10;
          int[] p={5,5,3,4,3};
          int[] g={400,500,200,300,350};
          System.out.println("最优受益:"+getBestGoldMining(w,g.length,p,g));
      }
  
      private static int getBestGoldMining(int w, int n, int[] p, int[] g) {
          //当可选的金矿为0 或者 工人数为0
          if (w==0 || n==0){
              return 0;
          }
          //当工人的数量不足以满足当前这座金矿需要的工人时
          if (w<p[n-1]){
              return getBestGoldMining(w,n-1,p,g);
          }
          return Math.max(getBestGoldMining(w,n-1,p,g),
                  getBestGoldMining(w-p[n-1],n-1,p,g)+g[n-1]);
      }
  }

• 递归的方式可能不太好理解，其实就是把你要的结果分成一个小的结果，类似于二叉树的方式，从叶子结点找到根节点就是我们要的值，这种方式不好理解，那么我换一种方式

• 使用二维数组的方式：

• 
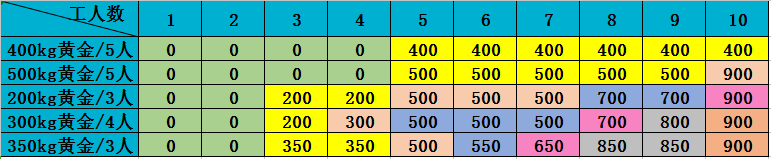
• 表格的横坐标是工人数在代码中用 w 表示，纵坐标是金矿储量在代码中用g数组表示

• public class text{
      /**
       * 获得金矿最优受益
       * @param: w   工人数量
       * @param: n   可选金矿数量
       * @param: p[] 金矿开采所需的工人数量
       * @param: g[] 金矿储量
       */
      public static void main(String[] args) {
  
          int w=10;
          int[] p={5,5,3,4,3};
          int[] g={400,500,200,300,350};
          System.out.println("最优受益:"+getBestGoldMining(w,p,g));
      }
      private static int getBestGoldMining(int w, int[] p, int[] g) {
          //1、创建二维数组
          int[][] resultTable=new int[g.length+1][w+1];
          //填充表格
          //代码中有两层循环第一个 for 循环每座金矿的储量
          //按照一行一行循环，对于二维数组
          for (int i=1;i<g.length+1;i++){
              //第二个 for 循环工人数
              for (int j=1;j<w+1;j++){
                  //当前这座金矿不满足开采人数时，那么把当前值的前一个位置的值赋给当前值
                  if (j<p[i-1]){
                      resultTable[i][j]=resultTable[i-1][j];
                  }else {     //满足开采人数
                      //resultTable[i-1][j]:当前位置的上头顶的那个元素
                      //resultTable[i-1][j-p[i-1]]+g[i-1]:这一行是找到上一步的局部最优解
                      resultTable[i][j]=Math.max(resultTable[i-1][j],
                              resultTable[i-1][j-p[i-1]]+g[i-1]);
                  }
              }
          }
          return resultTable[g.length][w];
      }
  }

• 改进二维数组：

• 降低空间复杂度到O(n)

• public class text{
      /**
       * 获得金矿最优受益
       * @param: w   工人数量
       * @param: n   可选金矿数量
       * @param: p[] 金矿开采所需的工人数量
       * @param: g[] 金矿储量
       */
      public static void main(String[] args) {
  
          int w=10;
          int[] p={5,5,3,4,3};
          int[] g={400,500,200,300,350};
          System.out.println("最优受益:"+getBestGoldMining(w,p,g));
      }
      private static int getBestGoldMining(int w, int[] p, int[] g) {
          //1、创建结果数组
          int[] results=new int[w+1];
          //2、填充一维数组
          for (int i=1;i<g.length+1;i++){
              for (int j=w;j>0;j--){
                  if (j>=p[i-1]){
                      results[j]=Math.max(results[j],
                              results[j-p[i-1]]+g[i-1]);
                  }
              }
          }
          //3、返回数组最后一个位置的值
          return results[w];
      }
  }