数据结构与算法之归并排序-优快云博客

本文详细介绍了归并排序算法的工作原理，包括其稳定性和时间复杂度。通过分治策略，归并排序将数据序列拆分成两部分分别排序，然后合并成一个有序序列。文中提供了一个完整的C语言实现示例，展示了如何使用递归进行归并排序，并给出了运行结果。

数据结构与算法之归并排序

前提条件

熟悉C语言与指针
熟悉数据结构与算法

简介

归并排序（Merge Sort）是建立在归并操作上的一种有效，稳定的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。
归并排序是稳定的排序.
时间复杂度 $O (n l o g n)$ ，空间复杂度为 $O (n)$ .

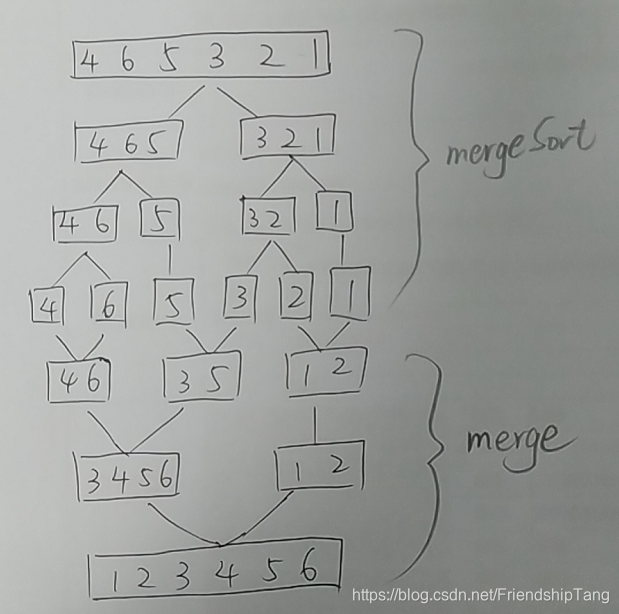
归并排序算法

void merge(int data[],int low,int mid,int high)
/*将有序子序列data[low..mid-1]和data[mid..high]归并为有序序列data[low..high]*/
{
    int i,p,k;
    int *tmp;
    tmp = (int *)malloc((high-low+1)*sizeof(int));
    if(!tmp) exit(0);
    k=0;
    for ( i = low,p = mid; i < mid&&p<=high;)
    {
        if(data[i]<data[p])
        {
            tmp[k++]=data[i++];
        }
        else
        {
            tmp[k++]=data[p++];
        }        
    }
    while (i<mid)
    {
        tmp[k++]=data[i++];
    }
    while (p<=high)
    {
        tmp[k++]=data[p++];
    }
    i = low;
    p=0;
    while (p<k)
    {
        data[i++]=tmp[p++];
    }
}

void mergeSort(int data[],int s,int t)
/*对data[s..t]进行归并排序*/
{
    int m;
    if(s<t){
        m=(s+t)/2;/*将data[s..t]均分为data[s..m]和data[m+1..t]*/
        mergeSort(data,s,m);/*递归地将data[s..m]进行归并排序*/
        mergeSort(data,m+1,t);/*递归地将data[m+1..t]进行归并排序*/
        merge(data,s,m+1,t);/*将data[s..m]和ata[m+1..t]归并为data[s..t]*/
    }
}

在这里插入图片描述

完整代码

#include<stdio.h>
#include<stdlib.h>

void merge(int data[],int low,int mid,int high)
/*将有序子序列data[low..mid-1]和data[mid..high]归并为有序序列data[low..high]*/
{
    int i,p,k;
    int *tmp;
    tmp = (int *)malloc((high-low+1)*sizeof(int));
    if(!tmp) exit(0);
    k=0;
    for ( i = low,p = mid; i < mid&&p<=high;)
    {
        if(data[i]<data[p])
        {
            tmp[k++]=data[i++];
        }
        else
        {
            tmp[k++]=data[p++];
        }        
    }
    while (i<mid)
    {
        tmp[k++]=data[i++];
    }
    while (p<=high)
    {
        tmp[k++]=data[p++];
    }
    i = low;
    p=0;
    while (p<k)
    {
        data[i++]=tmp[p++];
    }
}

void mergeSort(int data[],int s,int t)
/*对data[s..t]进行归并排序*/
{
    int m;
    if(s<t){
        m=(s+t)/2;/*将data[s..t]均分为data[s..m]和data[m+1..t]*/
        mergeSort(data,s,m);/*递归地将data[s..m]进行归并排序*/
        mergeSort(data,m+1,t);/*递归地将data[m+1..t]进行归并排序*/
        merge(data,s,m+1,t);/*将data[s..m]和ata[m+1..t]归并为data[s..t]*/
    }
}


int main(){
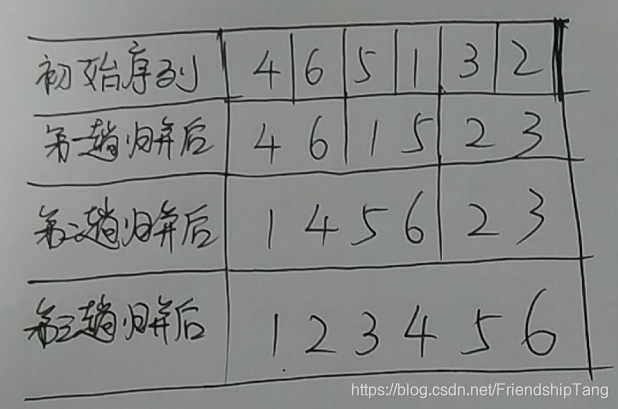
    int data[6]={4,6,5,1,3,2};
    mergeSort(data,0,5);
    printf("the result of the mergeSort:\n");
    for (int i = 0; i < 6; i++)
    {
        printf("%d ",data[i]);
    }
    printf("\n");
    system("pause");
    return 0;
}