《统计学习方法》学习笔记15：奇异值分解

简介

• 奇异值分解(singular value decomposition,SVD)是一种矩阵因子分解方法，是线性代数的概念，但在统计学习中被广泛使用，成为其重要工具。本书介绍的主成分分析、潜在语义分析都用到奇异值分解。
• 任意一个m x n矩阵，都可以表示为三个矩阵的乘积(因子分解)形式，分别是m阶正交矩阵、由降序排列的非负的对角线元素组成的m x n矩形对角矩阵和n阶正交矩阵，称为该矩阵的奇异值分解。矩阵的奇异值分解一定存在，但不唯一。奇异值分解可以看作是矩阵数据压缩的一种方法，即用因子分解的方式近似地表示原始矩阵，这种近似是在平方损失意义下的最优近似。

定义与性质

定义与定理

• 定义 (奇异值分解) 矩阵的奇异值分解是指，将一个非零的$m\times n$实矩阵$A，A\in R_{m\times n}$，表示为以下三个实矩阵乘积形式的运算，即进行矩阵的因子分解:
• $A=U\Sigma V^T$
• 其中$U$是$m$阶正交矩阵(orthogonal matrix )，$V$是$n$ 阶正交矩阵，又是由降序排列的非负的对角线元素组成的$m\times n$矩形对角矩阵(rectangular diagonal matrix)，满足
• $U{U}^T=I$
• $V{V}^T=I$
• $\Sigma =diag({\sigma }_1,{\sigma }_2,...,{\sigma }_p)$
• ${\sigma }_1\ge {\sigma }_2\ge ...\ge {\sigma }_p\ge 0$
• $p=min(m,n)$
• $U\Sigma V^T$称为矩阵A的奇异值分解( singular value decomposition，SVD )，${\sigma }_i$称为矩阵A的奇异值( singular value )，$U$的列向量称为左奇异向量(left singular vector )，$V$的列向量称为右奇异向量( right singular vector )。
• 注意：奇异值分解不要求矩阵A是方阵，事实上矩阵的奇异值分解可以看作是方阵的对角化的推广。
• 例如，给定一个$5\times 4$的矩阵$A$
  $A=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 0& 4\\ 0& 3& 0& 0\\ 0& 0& 0& 0\\ 2& 0& 0& 0\end{array}\right]$
• 它的奇异值分解由三个矩阵的乘积$U\Sigma V^T$给出，矩阵$U,\Sigma ,V^T$分别为
  $U=\left[\begin{array}{ccccc}0& 0& \sqrt{0.2}& 0& \sqrt{0.8}\\ 1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& \sqrt{0.8}& 0& -\sqrt{0.2}\end{array}\right]$
  $\Sigma =\left[\begin{array}{cccc}4& 0& 0& 0\\ 0& 3& 0& 0\\ 0& 0& \sqrt{5}& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]$
  $V^T=\left[\begin{array}{cccc}0& 0& 0& 1\\ 0& 1& 0& 0\\ 1& 0& 0& 0\\ 0& 0& 1& 0\end{array}\right]$
• 矩阵$\Sigma$是对角矩阵，对角线外的元素都是0，对角线上的元素非负，按降序排列。矩阵$U$和$V$是正交矩阵，它们与各自的转置矩阵相乘是单位矩阵，即
  $U{U}^T=I_5$，$V{V}^T=I_4$
• 矩阵的奇异值分解不是唯一的。矩阵$U$还可以为
  $U=\left[\begin{array}{ccccc}0& 0& \sqrt{0.2}& \sqrt{0.4}& \sqrt{0.8}\\ 1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 0& \sqrt{0.5}& \sqrt{0.5}\\ 0& 0& \sqrt{0.8}& -\sqrt{0.1}& -\sqrt{0.1}\end{array}\right]$
• 满足$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^T$
• 基本定理：任意给定一个实矩阵，其奇异值分解一定存在

紧奇异值分解与截断奇异值分解

• $A=U\Sigma V^T$又称为矩阵的完全奇异值分解(full singular value decomposition)。
• 实际常用的是奇异值分解的紧凑形式和截断形式。
• 紧奇异值分解是与原始矩阵等秩的奇异值分解
• 截断奇异值分解是比原始矩阵低秩的奇异值分解。
• 矩阵的秩-百度百科

紧奇异值分解

定义

设有$m\times n$实矩阵A，其秩为$rank(A)=T，r\le min(m,n)$，则称$U_r{\Sigma }_r{V}_r^T$为$A$的紧奇异值分解(compact singular value decomposition)，即

• $A=U_r{\Sigma }_r{V}_r^T$
• 其中，$U_r$是$m\times r$矩阵，$V_r$是$n\times r$矩阵，${\Sigma }_r$是$r$阶对角矩阵;矩阵$U_r$由完全奇异值分解中$U$的前$r$列、矩阵$V$由$V$的前$r$列、矩阵${\Sigma }_r$由$\Sigma$的前$r$个对角线元素得到。紧奇异值分解的对角矩阵${\Sigma }_r$的秩与原始矩阵$A$的秩相等。
• 例如，给定一个矩阵$A$的秩为$r=3$
  $A=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 0& 4\\ 0& 3& 0& 0\\ 0& 0& 0& 0\\ 2& 0& 0& 0\end{array}\right]$
• A的紧奇异值分解是$A=U_r{\Sigma }_r{V}_r^T$
• 其中
  $U_r=\left[\begin{array}{ccc}0& 0& \sqrt{0.2}\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 0\\ 0& 0& \sqrt{0.8}\end{array}\right]$
  ${\Sigma }_r=\left[\begin{array}{ccc}4& 0& 0\\ 0& 3& 0\\ 0& 0& \sqrt{5}\end{array}\right]$
  $V_r^T=\left[\begin{array}{cccc}0& 0& 0& 1\\ 0& 1& 0& 0\\ 1& 0& 0& 0\end{array}\right]$
• 满足$A_{m\times n}=U_{m\times r}{\Sigma }_{r\times r}{V}_{r\times n}^T$,其中$r$表示矩阵$A$的秩

截断奇异值分解

在矩阵的奇异值分解中，只取最大的$k$个奇异值($k<r,r$为矩阵的秩)对应的部分，就得到矩阵的截断奇异值分解。实际应用中提到矩阵的奇异值分解时，通常指截断奇异值分解。

定义

设$A$为$mxn$实矩阵，其秩$rank(A)=r$，且$0<k<r$，则称$U_k{\Sigma }_k{V}_k^T$为矩阵$A$的截断奇异值分解( truncated singular value decomposition)

• $A\approx U_k{\Sigma }_k{V}_k^T$
• 其中$U_k$是$m\times k$矩阵，$V_k$是$n\times k$矩阵，${\Sigma }_k$是$k$阶对角矩阵;矩阵$U_k$由完全奇异值分解中$U$的前$k$列、矩阵$V$由$V$的前$k$列、矩阵由${\Sigma }_k$的前$k$个对角线元素得到。对角矩阵${\Sigma }_k$的秩比原始矩阵A的秩低。
• 例如，给出一个矩阵$A$
  $A=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 0& 4\\ 0& 3& 0& 0\\ 0& 0& 0& 0\\ 2& 0& 0& 0\end{array}\right]$
• $A$的秩为3，若取$k=2$则其截断奇异值分解是$A\approx A_2=U_2{\Sigma }_2{V}_2^T$
• 其中
  $U_2=\left[\begin{array}{cc}0& 0\\ 1& 0\\ 0& 1\\ 0& 0\\ 0& 0\end{array}\right]$
  ${\Sigma }_2=\left[\begin{array}{cc}4& 0\\ 0& 3\end{array}\right]$
  $V_2^T=\left[\begin{array}{cccc}0& 0& 0& 1\\ 0& 1& 0& 0\end{array}\right]$
  $A_2=U_2{\Sigma }_2{V}_2^T=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 4\\ 0& 3& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]$
• 满足$A_{m\times k}=U_{m\times k}{\Sigma }_{k\times k}{V}_{k\times n}^T$,$0<k<r$,其中,$r$表示矩阵$A$的秩

几何意义

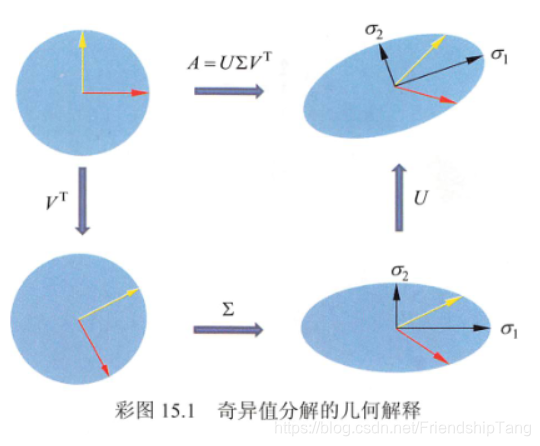
• 从线性变换的角度理解奇异值分解，$m\times n$矩阵$A$表示从$n$维空间$R^n$到$m$维空间$R^m$的一个线性变换，
  • $T:x\to Ax$
• $x\in R^n，Ax\in R^m$，$x$和 $Ax$分别是各自空间的向量。线性变换可以分解为三个简单的变换:一个坐标系的旋转或反射变换($V^T$)、一个坐标轴的缩放变换($\Sigma$)、另一个坐标系的旋转或反射变换($U$)。奇异值定理保证这种分解一定存在。这就是奇异值分解的几何解释。
• 任意一个向量$x\in R^n$，经过基于$A=U\Sigma V^T$的线性变换，等价于经过坐标系的旋转或反射变换$V^T$，坐标轴的缩放变换$\Sigma$，以及坐标系的旋转或反射变换$U$，得到向量$Ax\in R^m$。
• 上图给出直观的几何解释。原始空间的标准正交基(红色与黄色)，经过坐标系的旋转变换$V^T$、坐标轴的缩放变换$\Sigma$(黑色${\sigma }_1,{\sigma }_2$)、坐标系的旋转变换$U$，得到和经过线性变换$A$等价的结果。
• 例如，给定一个2阶矩阵
  $A=\left[\begin{array}{cc}3& 1\\ 2& 1\end{array}\right]$
• 其奇异值分解为
  $U=\left[\begin{array}{cc}0.8174& -0.5760\\ 0.5760& 0.8174\end{array}\right],\Sigma =\left[\begin{array}{cc}3.8643& 0\\ 0& 0.2588\end{array}\right],V^T=\left[\begin{array}{cc}0.9327& 0.3606\\ -0.3606& 0.9327\end{array}\right]$
• 观察基于矩阵$A$的奇异值分解将$R^2$的标准正交基
  $e_1=\left[\begin{array}{c}1\\ 0\end{array}\right],e_2=\left[\begin{array}{c}0\\ 1\end{array}\right]$
• 进行线性转换的情况。
  • 首先,$V^T$表示一个旋转变换,将标准正交基$e_1，e_2$旋转，得到向量$V^T{e}_1,V^T{e}_2$:
    $V^T{e}_1=\left[\begin{array}{c}0.9327\\ -0.3606\end{array}\right],V^T{e}_2=\left[\begin{array}{c}0.3606\\ 0.9327\end{array}\right]$
  • 其次，$\Sigma$表示一个缩放变换，将向量$V^T{e}_1,V^T{e}_2$在坐标轴方向缩放${\sigma }_1$倍和${\sigma }_2$倍，得到向量$\Sigma V^T{e}_1,\Sigma V^T{e}_2$:
    $\Sigma V^T{e}_1=\left[\begin{array}{c}3.6042\\ -0.0933\end{array}\right],\Sigma V^T{e}_2=\left[\begin{array}{c}1.3935\\ 0.2414\end{array}\right]$
  • 最后，$U$表示一个旋转变换，再将向量$\Sigma V^T{e}_1,\Sigma V^T{e}_2$旋转，得到向量$U\Sigma V^T{e}_1,U\Sigma V^T{e}_2$，也就是向量$A{e}_1和A{e}_2$:
    $A{e}_1=\left[\begin{array}{c}3\\ 2\end{array}\right],A{e}_2=\left[\begin{array}{c}1\\ 1\end{array}\right]$
• 综上，矩阵的奇异值分解也可以看作是将其对应的线性变换分解为旋转变换、缩放变换及旋转变换的组合。经验证，这个变换的组合一定存在。

奇异值分解的计算

• 奇异值分解基本定理证明的过程蕴含了奇异值分解的计算方法。矩阵A的奇异值分解可以通过求对称矩阵$A^{T}A$的特征值和特征向量得到。$A^{T}A$的特征向量构成正交矩阵$V$的列;$A^{T}A$的特征值${\lambda }_j$的平方根为奇异值${\sigma }_i$，即
• ${\sigma }_j=\sqrt{{\lambda }_j},j=1,2,...,n$
• 对其由大到小排列作为对角线元素，构成对角矩阵$\Sigma$;求正奇异值对应的左奇异向量，再求扩充的$A^T$的标准正交基，构成正交矩阵$U$的列。从而得到$A$的奇异值分解$A=U\Sigma V^T$

计算过程

给定$m\times n$矩阵$A$，可以按照上面的叙述写出矩阵奇异值分解的计算过程。

1. 首先求$A^{T}A$的特征值和特征向量。
   计算对称矩阵$W=A^{T}A$
   求解特征方程$(W-\lambda I)x=0$
   得到特征值${\lambda }_i$，并将特征值由大到小排列${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_n\ge 0$
   将特征值${\lambda }_i(i=1,2,\dots ,n)$代入特征方程求得对应的特征向量。

2. 求$n$阶正交矩阵$V$
   将特征向量单位化，得到单位特征向量$v_1,v_2,\dots ,v_n$，$n$阶正交矩阵$V$:
   $V=\left[\begin{array}{cccc}{v}_1& v_2& \dots & v_n\end{array}\right]$

3. 求$m\times n$对角矩阵$\Sigma$
   计算$A$的奇异值${\sigma }_j=\sqrt{{\lambda }_j},j=1,2,...,n$
   构造$m\times n$矩形对角矩阵$\Sigma$，主对角线元素是奇异值，其余元素是零，
   $\Sigma =diag({\sigma }_1,{\sigma }_2,...,{\sigma }_n)$

4. 求$m$阶正交矩阵$U$
   对$A$的前$r$个正奇异值,令$u_j=\frac{1}{{\sigma }_j}A{v}_j,j=1,2,...,r$
   得到$U_1=\left[\begin{array}{cccc}{u}_1& u_2& \dots & u_r\end{array}\right]$
   求$A^T$的零空间的一组标准正交基{$u_{r+1},u_{r+2},...,u_m,$},令
   $U_2=\left[\begin{array}{cccc}{u}_{r+1}& u_{r+2}& ...& u_m\end{array}\right]$
   并令 $U=\left[\begin{array}{cc}{U}_1& U_2\end{array}\right]$

5. 得到奇异值分解$A=U\Sigma V^T$

例：求矩阵$A=\left[\begin{array}{cc}1& 1\\ 2& 2\\ 0& 0\end{array}\right]$的奇异值分解。
解：

• 求$A^{T}A$的特征值和特征向量
  $A^{T}A=\left[\begin{array}{ccc}1& 2& 0\\ 1& 2& 0\end{array}\right]\left[\begin{array}{cc}1& 1\\ 2& 2\\ 0& 0\end{array}\right]=\left[\begin{array}{cc}5& 5\\ 5& 5\end{array}\right]$
  特征值$\lambda$和特征向量$x$满足特征方程$(A^{T}A-\lambda I)x=0$
  得到齐次线性方程组
  $\{\begin{array}{l}(5-\lambda )x_1+5x_2=0\\ 5x_1+(5-\lambda )x_2=0\end{array}$
  该方程组有非零解的充要条件是
  $\left|\begin{array}{cc}5-\lambda & 5\\ 5& 5-\lambda \end{array}\right|=0$
  即 ${\lambda }_2-10\lambda =0$
  解此方程，得矩阵$A^{T}A$的特征值${\lambda }_1=10,{\lambda }_2=0$。
  将特征值${\lambda }_1=10,{\lambda }_2=0$分别代入线性方程组，得到相对应的单位特征向量$v_1=\left[\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right],v_2=\left[\begin{array}{c}\frac{1}{\sqrt{2}}\\ -\frac{1}{\sqrt{2}}\end{array}\right]$
• 求正交矩阵$V$
  构造正交矩阵$V$
  $V=\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\end{array}\right]$
• 求对角矩阵$\Sigma$
  奇异值为${\sigma }_1=\sqrt{{\lambda }_1}=\sqrt{10}$和${\sigma }_2=0$。
  构造对角矩阵$\Sigma =\left[\begin{array}{cc}\sqrt{10}& 0\\ 0& 0\\ 0& 0\end{array}\right]$
  注意：在$\Sigma$中要加上零行向量，使得$\Sigma$能够与$U,V$进行矩阵乘法运算。
• 求正交矩阵$U$
  基于$A$的正奇异值计算得到列向量$u_1$
  $u_1=\frac{1}{{\sigma }_1}A{v}_1=\frac{1}{\sqrt{10}}\left[\begin{array}{cc}1& 1\\ 2& 2\\ 0& 0\end{array}\right]\left[\begin{array}{c}\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}\end{array}\right]=\left[\begin{array}{c}\frac{1}{\sqrt{5}}\\ \frac{2}{\sqrt{5}}\\ 0\end{array}\right]$
  列向量$u_2，u_3$是$A^T$的零空间$N(A^T)$的一组标准正交基。为此，求解以方程组
  $A^{T}x=\left[\begin{array}{ccc}1& 2& 0\\ 1& 2& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$
  即 $x_1+2x_2+0x_3=0$得$x_1=-2x_2+0x_3$
  分别取$(x_2,x_3)$为$(1,0)和(0,1)$得到$N(A^T)$的基$(-2,1,0{)}^T,(0,0,1{)}^T$
  $N(A^T)$的一组标准正交基是$u_2=(-\frac{2}{\sqrt{5}},\frac{1}{\sqrt{5}},0{)}^T,u_3=(0,0,1{)}^T$
  构造正交矩阵$U$
  $U=\left[\begin{array}{ccc}\frac{1}{\sqrt{5}}& -\frac{2}{\sqrt{5}}& 0\\ \frac{2}{\sqrt{5}}& \frac{1}{\sqrt{5}}& 0\\ 0& 0& 1\end{array}\right]$
• 矩阵$A$的奇异值分解
  $A=U\Sigma V^T=\left[\begin{array}{ccc}\frac{1}{\sqrt{5}}& -\frac{2}{\sqrt{5}}& 0\\ \frac{2}{\sqrt{5}}& \frac{1}{\sqrt{5}}& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cc}\sqrt{10}& 0\\ 0& 0\\ 0& 0\end{array}\right]\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\end{array}\right]$

Python Numpy实现奇异值分解

import numpy as np
# 奇异值分解SVD
A = np.mat([[1,1], [2,2],[0,0]])
print("A:",A)
U,Sigma,V_T = np.linalg.svd(A)
print("U:\n",U)
print("Sigma:\n",Sigma)
print("V_T:\n",V_T)
# 还原
Sigma_3x2 = np.mat([Sigma,[0,0],[0,0]])
print("Sigma_3x2:\n",Sigma_3x2)
A_restore = U * Sigma_3x2 * V_T
print("A_restore:\n",A_restore)

输出结果

参考文献

[1] 李航.统计学习方法(第二版)[M], 清华大学出版社, 2019.ISBN 978-7-302-51727-6