BEGAN

《BEGAN: Boundary Equilibrium Generative Adversarial Networks》

github

---

背景

在传统的GAN中，虽然提供了一种新的方法来学习数据分布，也取得了相比以前的方法不错的效果，但是它仍存在以下的几个问题：

• 即便使用很多的训练技巧，GAN仍然很难训练
• 模型的超参数的选择对于模型最终的效果十分重要
• 难以控制生成图像的质量和多样性
• 难以平衡判别器和生成器之间的收敛
• GAN易出现梯度消失和模式坍缩问题

针对于这些问题，作者提出了一种基于均衡思想的GAN的变体BEGAN，它相对于其他的GANs的贡献或是优势在于：

• 一个简单且鲁棒性更好的 GAN 架构，使用标准的训练步骤实现了快速、稳定的收敛，生成的图像质量更高
• 提出了一种均衡的概念，使得判别器和生成器在训练过程中保持平衡
• 一种控制在图像多样性与视觉质量之间权衡的新方法
• 提出了用于衡量收敛的方法
• 提出了一个由Wasseratein loss衍生而来的配套的loss

---

损失函数

在BEGAN出现之前，DCGAN使用了卷积结构来提高生成图像的质量；EBGAN提高收敛的稳定性和模型的鲁棒性；WGAN提高了稳定性和更好的模式覆盖，但是收敛速度慢。

上述的这些GAN的变体以及其他的GAN相关的模型，都是基于训练数据实现的一种直接匹配，希望生成模型的数据分布$p_G$尽可能的接近真实数据分布$p_{data}$。而BEGAN中提出了另一种思路，它使用了自动编码器（auto-encoder）做为判别器$D$ ，它所做的是尽可能地匹配误差的分布而不是直接匹配样本的分布，如果误差的分布之间足够的接近，那么真实的样本之间的分布也会足够的接近，生成的结果质量同样也不差。

下面先介绍一下训练一个pixel-wise的自编码器的损失如下所示：
L ( v ) = ∣ v − D ( v ) ∣ η  where  { D : R N x ↦ R N x  is the autoencoder function.  η ∈ { 1 , 2 }  is the target norm.  v ∈ R N x  is a sample of dimension  N x \mathcal{L}(v)=|v-D(v)|^{\eta} \text { where } \left\{\begin{array}{l}{D : \mathbb{R}^{N_{x}} \mapsto \mathbb{R}^{N_{x}}} & {\text { is the autoencoder function. }} \\ {\eta \in\{1,2\}} & {\text { is the target norm. }} \\ {v \in \mathbb{R}^{N_{x}}} & {\text { is a sample of dimension } N_{x}}\end{array}\right. L(v)=∣v−D(v)∣η where ⎩⎨⎧​D:RNx​↦RNx​η∈{1,2}v∈RNx​​ is the autoencoder function.  is the target norm.  is a sample of dimension Nx​​

• ${\mu }_1、{\mu }_2$ :表示自动编码器loss的两个分布，即真实样本损失的分布和生成样本损失的分布
• $\Gamma ({\mu }_1,{\mu }_2)$：表示${\mu }_1$和${\mu }_2$的所有组合的集合
• $m_1、m_2$：表示各自的均值

有了上述的的规定后，Wasserstein distance可以定义为：
$$W_1\left({\mu }_1,{\mu }_2\right)=\underset{\gamma \in \Gamma \left({\mu }_1,{\mu }_2\right)}{\inf }{\mathbb{E}}_{\left(x_1,x_2\right)\sim \gamma }\left[\left|x_1-x_2\right|\right]$$
那么它的下界为：
$$\inf \mathbb{E}\left[\left|x_1-x_2\right|\right]⩾\inf \left|\mathbb{E}\left[x_1-x_2\right]\right|=\left|m_1-m_2\right|$$
BEGAN中$G$和$D$对应的损失函数为：
$$\{\begin{array}{ll}{\mathcal{L}}_D=\mathcal{L}\left(x;{\theta }_D\right)-\mathcal{L}\left(G\left(z_D;{\theta }_G\right);{\theta }_D\right)& \text{ for }{\theta }_D\\ {\mathcal{L}}_G=-{\mathcal{L}}_D& \text{ for }{\theta }_G\end{array}$$

---

均衡

当$D$无法判别样本的来源时，真实样本和生成样本错误的分布就应该是一样的，即它们的期望误差应该相等
$$\mathbb{E}[\mathcal{L}(x)]=\mathbb{E}[\mathcal{L}(G(z))]$$
为了方便处理，引入超参数$\gamma$来放松限制，$\gamma$ 的定义如下：
$$\gamma =\frac{\mathbb{E}[\mathcal{L}(G(z))]}{\mathbb{E}[\mathcal{L}(x)]}$$
在EBGAN中，我们希望$D$既可以对真实图像自动编码，又可以正确的判别输入的样本。$\gamma$ 的引入就是平衡这两种要求的，例如当$\gamma$很小时，说明分母部分值很大，那么此时模型专注于识别的正确率，导致$G$只生成已经可以欺骗$D$的图像，这时就会出现模式坍缩问题。因此，$\gamma$ 也可以称为多样性比率（diversity ratio）。

---

边界均衡思想

BEGAN的目标为：
$$\{\begin{array}{ll}{\mathcal{L}}_D=\mathcal{L}(x)-k_t\cdot \mathcal{L}\left(G\left(z_D\right)\right)& \text{ for }{\theta }_D\\ {\mathcal{L}}_G=\mathcal{L}\left(G\left(z_G\right)\right)& \text{ for }{\theta }_G\\ k_{t+1}=k_t+{\lambda }_k\left(\gamma \mathcal{L}(x)-\mathcal{L}\left(G\left(z_G\right)\right)\right)& \text{ for each training step }t\end{array}$$
其中$k_t$控制在梯度下降过程中对$D$判别能力的重视程度，${\lambda }_k$表示学习率。

然后使用Adam优化器独立的更新$G$和$D$。

此外，作者还提出了一种新的对于GAN收敛性的测度。在传统的GAN中，只能通过迭代次数或是直观的看生成图像的效果来判断收敛。这里作者提出了一种全局收敛测度方式，同时也是使用了均衡的思想，我们可以构建收敛过程，先找到比例控制算法$(|\gamma \mathcal{L}(x)-\mathcal{L}(G(z_G))|)$的瞬时过程误差，然后找到该误差的最低绝对值的最接近重建$(\mathcal{L}(x))$。该测度可以形式化为两项的和：
$${\mathcal{M}}_{global}=\mathcal{L}(x)+\left|\gamma \mathcal{L}(x)-\mathcal{L}\left(G\left(z_G\right)\right)\right|$$
通过${\mathcal{M}}_{global}$的值就可以判断模型是否收敛了。

---

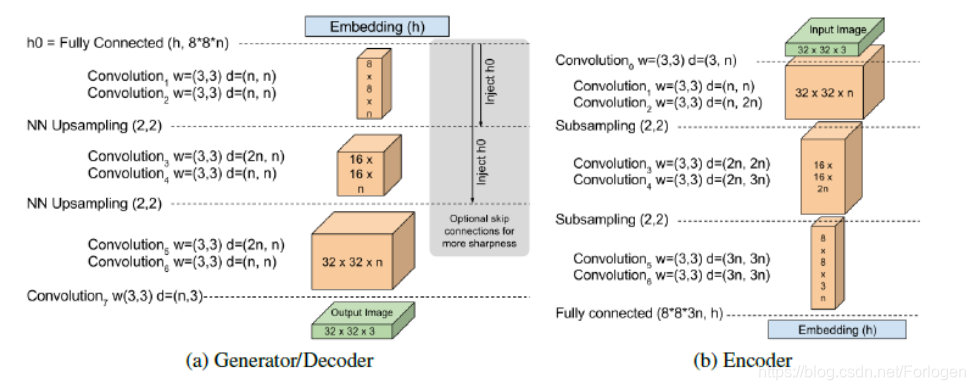
模型架构

BEGAN 的架构十分简单，几乎所有都是 3×3 卷积，sub-sampling 或者 upsampling，没有 dropout、批量归一化或者随机变分近似，如下所示

---

实验

针对于图像的多样性和生成图形的质量所做的实验的结果如下所示，从中可以看出EBGAN的效果远优于BEGAN

当我们改变$\gamma$ 的值时，模型生成结果的多样性和质量对比效果如下所示，从中可以看出，值越小，生成的图像越清晰，但是也更接近；值越大，多样性提高了，但是图像的质量同样也下降了

在生成图像的空间连续性方面，BEGAN的效果也要远优于其他的GANs

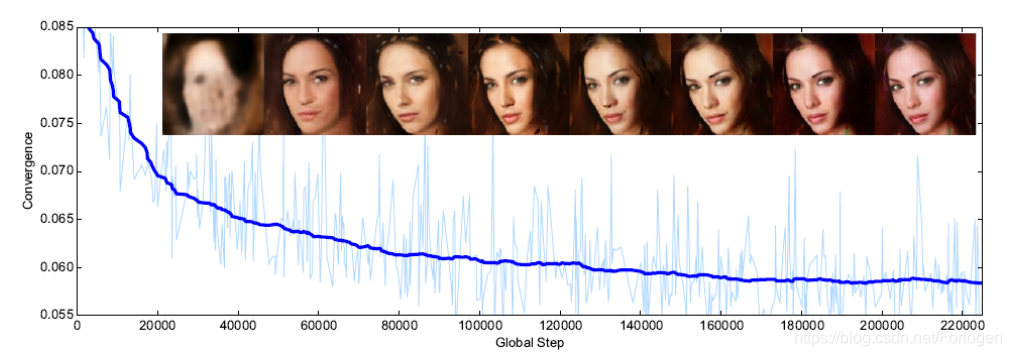
同时随着模型的逐渐收敛，我们可以看出，生成的图像的质量在不断地提升

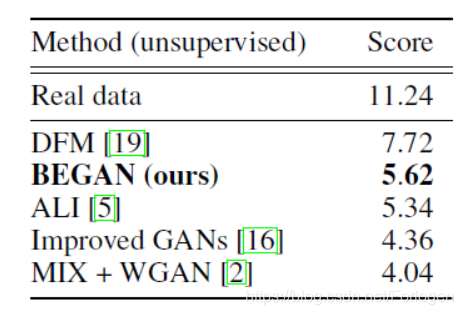
最后在数值实验中也显示了BEGAN的inception score更小

因此我们可以看出，BEGAN针对 GAN 训练难、控制生成样本多样性难、平衡鉴别器和生成器收敛难等问题，做出了很大的改善。

---

参考

http://www.dataguru.cn/article-11048-1.html

https://blog.youkuaiyun.com/linmingan/article/details/79912988

https://blog.youkuaiyun.com/qq_25737169/article/details/77575617

https://www.cnblogs.com/shouhuxianjian/p/10405147.html

https://blog.youkuaiyun.com/m0_37561765/article/details/77512692

https://blog.youkuaiyun.com/StreamRock/article/details/81023212