模型的偏差、方

最新推荐文章于 2025-06-02 21:49:23 发布

Forlogen

最新推荐文章于 2025-06-02 21:49:23 发布

阅读量1.6k

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/Forlogen/article/details/88384105

今天看书看到很多地方都讲到了方差和偏差的权衡，自己顿时感觉理解的不是很清晰，很多细节都想不起来了，所以整理一下，一位加深理解，二为往后的回顾，GO ! _{_}

首先看一下有关模型误差相关方面的表述，下图是《统计学习方法》中关于误差的相关整理

偏差和方差

1. 总览

对于某个特定的模型来说，它的泛化误差（Generation Error）可以分为三部分：模型预测值的方差（variance）、预测值相对真实值的偏差（bias）、样本本身存在的噪声（noise），可以用下面的公式进行表示： $E((y-\hat f(x))^2)=\sigma^2+Var[\hat f(x)]+(Bias[\hat f(x)])^2$

其中 $Bias[\hat f(x)]=E[\hat f(x)-f(x)]$

我们分别看一下泛化误差的这三个部分：
• 模型预测值相对真实值的偏差：直观上它是算法预测值和样本真实值之间的偏离程度，它反映了模型的拟合能力，偏差越大则模型的拟合能力越差，偏差越小的模型拟合能力越好，但是如果偏差小到一定程度则模型就可能会出现过拟合
• 模型预测值的方差：它反映模型在相同规模不同的训练集上的性能的波动情况，当模型具有低方差，则对于训练集变化的受影响较小，反之较大
• 样本本身存在的噪声：它是真实情况中不可避免的，因此它属于不可约减的误差（irreducible error），它反映了当前的训练集上任意的算法所能达到的额期望误差的下界，刻画了学习问题本身的难度

下面我们通过一个例子具体看一下：假设靶的中心是样本的真实值，左图镖的位置距离中心远，表示偏差大，但是位置相对集中，则方差较小；右图镖的位置相对左图距离中心更近，表示偏差较小，但是位置分散，表示方差较大。

相对于前面的公式表示，我们用图像化表示后就可以很直观的看到偏差、方差和噪声的情况。

2.公式推导

为了方便推导，先做如下的符号规定：
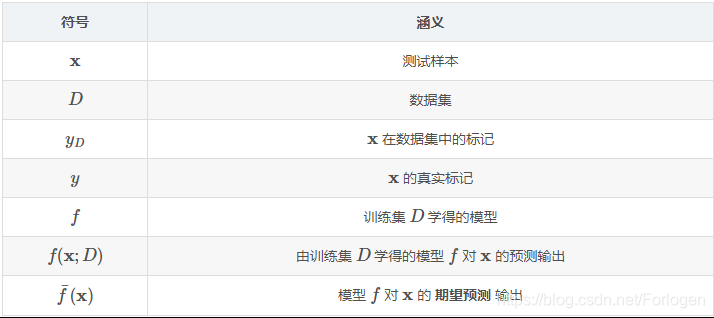
在这里插入图片描述

例如在回归模型中，定义的平方预测误差期望为： $Err(x)=E[y-f(x;D)^2]$

定义在训练集D上模型 f 对样本 X 的预测值为f(x;D)，那么f对X的期望预测如下： $\bar f(x) = E_{D}[f(x;D)]$

使用规模相同样本不同的训练集产生的方差为： $var(x)=E_{D}[(f(x;D)-\bar f(x))^2]$

而其中噪声为真实标记与数据集中的实际标记间的偏差： $\epsilon^2=E_{D}[(y_{D}-y)^2]$

期望预测值和真实标记的误差就是偏差： $bias^2(x)=(\bar f(x)-y)^2$

如果将算法的期望泛化误差进行分解，可以得到如下的结果：

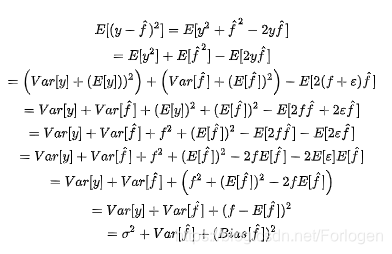
最后的三项分别是噪声的方差、模型预测值的方差、预测值相对于真实值的偏差

3.偏差-方差分解

从上面的分析我们可以看出，想让我们的模型同时拥有低偏差和低方差是不可能的，也被称为偏差-方差窘境。在模型训练的起始阶段，拟合效果差，则偏差较大，数据集的变化对于模型的影响也很小，表示方差较小；随着训练的深入，模型的拟合能力越来越强，偏差逐渐减小，方差逐渐增大；当模型训练的一定程度时，它的拟合能力非常强，这时的所有样本都可以很好的被拟合，偏差很小，但是训练集细微的变化都会对模型的效果产生很大的影响，方差就很大，则将发生过拟合。

一般来说：参数或者线性的机器学习算法一般都会有一个很高的偏差和一个很低的方差。但是，非参数或者非线性的机器学习算法一般都有一个很低的偏差和一个很高的方差。

所以，根据偏差-方差分解说明，泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。给定学习任务，为了取得好的泛化性能，则需使偏差较小，即能够充分的拟合数据，并且使方差较小，即使得数据扰动产生的影响小。故在实际使用中，我们需要在两者之间做一个权衡，使我们的模型效果达到最优。