林轩田机器学习技法第一讲-Linear Support Vector Machine

学习完了机器学习基石课程后，趁热打铁继续学习下机器学习技法的课程啦！完了就要专心看论文了~~~首先看一下两门课的共通点以及这门课所侧重的三个算法：SVM、Adaptive Boosting、Deep Learning，它们分别从不同的思想提出，各有千秋

了解之后，正式开始学习了！第一讲学习有关线性支持向量机的知识

首先我们回顾一下上门课程所学到的有关线性分类的东西，如下图所示，给定一系列不同类的数据点，我们希望可以找到一条线或是一个超平面可以很好将不同的点区分开来，相关的算法比如PLA、Pocket、LR等，在数学上其实是算一个加权的分数，然后利用$sign(x)$得出+1或是-1

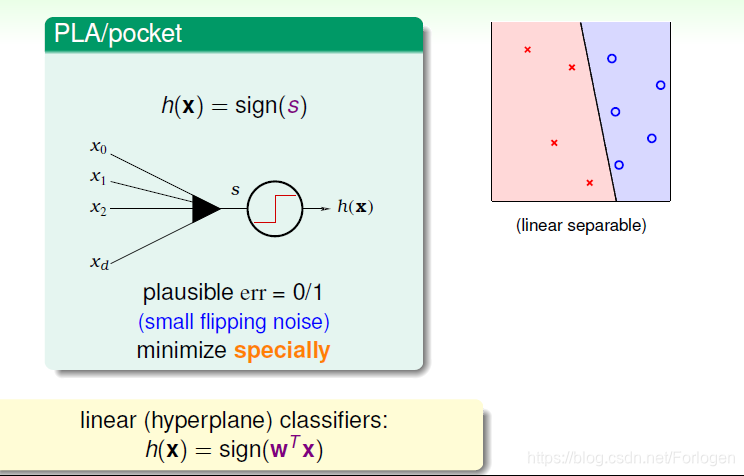
那么由于数据点不是完全贴合在一起的，那么可以找到的线理论上是有无数条的，如下图所示的情况，每一条线都可以正确的分类，那么如何找到最好的一条呢？

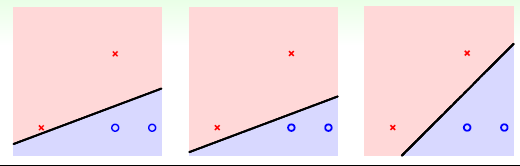
从算法分析可知，PLA等是随机的选择了一条；从VC Dimension的理论来看，也都满足$V{C}_{Bound}$的要求，而且模型的复杂度相同，泛化能力相同。但我们直观上来看，仿佛第三条线的效果更好，那有什么根据吗？

首先，我们将图像改为下图所示的形式，点周围的圆形区域表示分类线所能容忍的误差的程度，即区域面积越大，数据点到直线的距离越大，容忍误差的程度越强，反之越小。从另一个角度来看，可以将其形象的将其看成直线的胖瘦

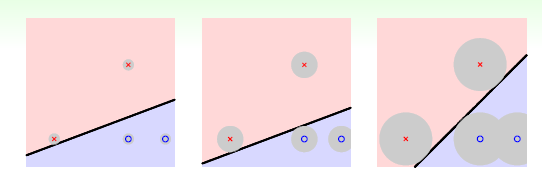
那么对于误差的容忍程度是什么意思呢？如果我们取到和图中数据$X_n$相近的新的数据 $x$ ,直线也可以将其正确的区分。这样的模型，既可以允许部分数据噪声的存在，也可以很好的避免过拟合的出现

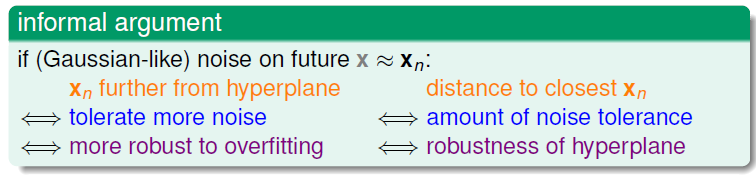
而且这里的胖指的是在正确划分的基础上，直线离两边数据点的最小距离。分类的线由$W$决定，我们的目标是找到使其最胖的时候所对应的$W$值

理论上把这种胖称之为$margin$，越胖表示$margin$越大。所以整体上来说，就是希望在满足如下条件的基础上，找到最大的$margin$对应的$W$，此时我们认为这条分类的线就是最好的！

因此在求解的目标中，最重要的就是通过求解$distance（X_n，W）$来求出最优的$W$

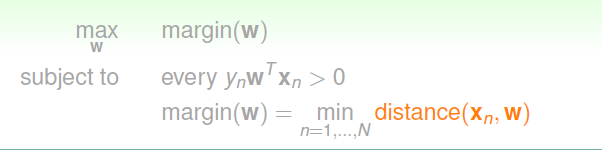
为了方便后面公式的推导，这里我们做一些新的规定：在$W$向量中，将$W_0$单独分离出来，将其记为$b$；在$X$向量中，不再令$X_0=1$，而是将其去掉，这样我们就得到了比之前矮一些的$W$和$X$

那么$h(x)$也就变成了如下的形式

---

接下来，看一下如何计算点到分类平面的距离。假设图中的超平面$w^{T}x+b=0$上有$x^{\prime }$和$x^{\prime \prime }$两个，那么必然满足公式$①$，那么$x^{\prime \prime }-x^{\prime }$就是超平面上的一个向量，而公式$②$结果为零，表示$W$是垂直于$x^{\prime \prime }-x^{\prime }$，也就是$W$是超平面的法向量。那么现在平面外有一点$x$，要计算$x$到平面的距离，根据数学的知识，我们知道可以计算$x-x^{\prime }$在法向量方向上的投影

令$x^{\prime \prime }-x^{\prime }$和$w$之间的夹角为$\theta$，根据三角函数的知识，距离的计算就可以通过下式求出

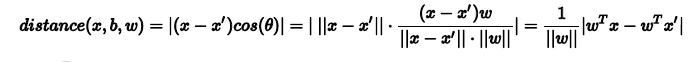
带入$①$式就可得如下得形式，它和$w$和$b$有关

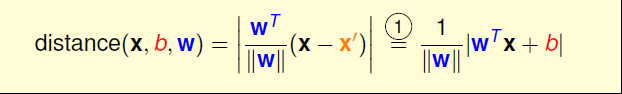
根据上面的条件我们知道，在分类平面已知的情况下，所有的点满足下图公式1，表示所有点都分对了。那么将其带入上面距离的计算公式，去掉绝对值后就是公式2的形式

这样经过转换，我们的求解目标就变成了下面这样，但是这样看来仍然有点抽象，我们很难求解

对于等式左右两边乘以一个相同的数，等式的结果是不变的，在这个问题中，也就是$w^{T}x+b=0$和$3w^{T}x+3b=0$表示的是同一个平面。因此将$w$和$b$进行放缩得到的平面不会发生改变，所以这里我们令距离分类最近的点满足下图公式2的形式，那么margin就变成了$\frac{1}{||w||}$

即求解目标为如下的形式，因为限制条件强化了，$y_n(W^T{x}_n+b)>0$就可以省略

上面公式的条件是$y_n(w^T{x}_n+b)=1$，也就是对所有的点要求$y_n(w^T{x}_n+b)\ge 1$，根据相关的理论证明可能这样放宽后得到的结果仍然满足最先的条件

所以将其转化为它的对偶问题，同时去掉根号，为了方便计算添加$\frac{1}{2}$，求解目标就如下图所示，形象化的来说就是找到那条分类正确的最胖的线

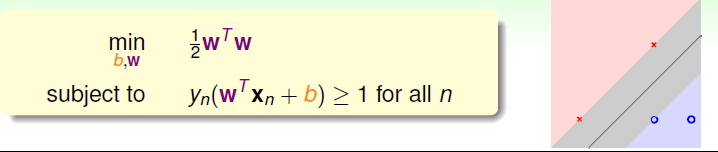
假设上右图中的四个点如下所示，将其表示成矩阵的形式，带入到条件中可得i、ii、iii、iv的形式，如果将i和iii合并可得$w_1\ge +1$，将ii和iv合并可得$w_2\le -1$，综合可得$\frac{1}{2}{w}^{T}w\ge 1$。那么如果$w1=1、w2=-1、b=-1$的话就有等于1 的情况，也就是得到了最优分类面的解，则分类面用$x_1-x_2-1=0$表示。则最后得到的g如下所示

何为Support Vector Machine(SVM)，即支持向量机呢？因为分类面仅仅由分类面的两边距离它最近的几个点决定的，其它点对分类面没有影响。故将决定分类面的几个点称之为支持向量（Support Vector），如下右图中方框中的点所示，而利用支持向量得到最佳分类面的方法叫支持向量机。

SVM的求解目标和条件如下所示，仔细一看好像无法使用梯度下降来求，但它是一个二次规划问题Quadratic Programming。

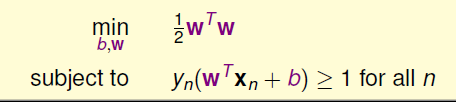
上面的目标表达式是关于w的二次函数，条件是关于$w$和$b$的一次函数，所以符合二次规划的特征。接下来就需找出SVM与标准二次规划问题的参数对应关系，如下图所示

这样我们就可以将整个过程总结如下
• 计算对应的二次规划参数$Q，p，A，c$
• 计算$b，w$
• 将$b和w$代入gsvm，得到最佳分类面
这里的向量机称为线性硬间隔支持向量机，线性是指数据集是线性可分的，硬间隔是指不允许有一个数据分错。

那如果像前面一样，我们的数据集是非线性可分的呢？这时学过的线性变换就配上用场了，将非线性可分的$x$域中的数据转换到$z$域中，变成线性可分的问题

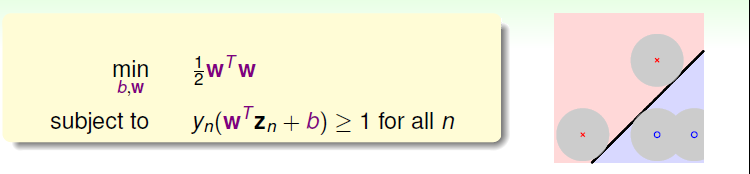
到现在看来，支持向量机的这种方式效果更好一些，那么在理论上是否有保证呢？SVM的这种思想其实与我们之前介绍的正则化思想很类似。regularization的目标是将$E_{in}$最小化，条件是$w^{T}w\le C$；SVM的目标是最小化$w^{T}w$，条件是$E_{in}=0$或是更严格的限制。哎这样看来，regularization与SVM的目标和限制条件分别对调了。其实两者考虑的内容是类似的，效果也是相近的。SVM也可以说是一种weight-decayregularization，限制条件是$E_{in}=0$

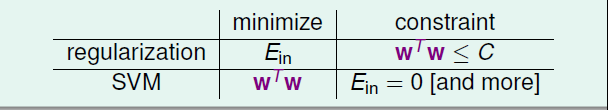
在之前VC Dimension的部分讲到，如果我们不限制线的胖瘦，像PLA将可以将任意的三个点shatter，可以有8种Dichotomies。但是如果线越胖，margin越大，那么它可能shatter的点就可能越少。故当dichotomies越少，VC Dimension就越小，模型的泛化能力就越强

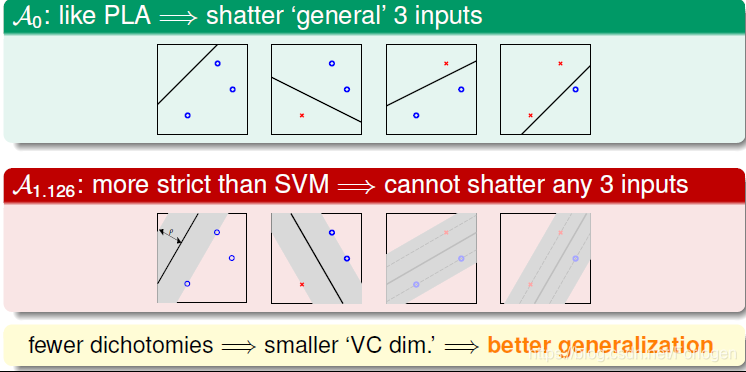
那为什么dichotomies越少，VC Dimension就越小呢？首先我们看一下硬间隔支持向量机的VC Dimension，记为$d_{vc}(A_{\rho })$。它是与数据有关的，而我们之前介绍的$d_{vc}$是与数据无关。

假如平面上有3个点分布在单位圆上，如果Margin为0，即$\rho$=0，这条细直线可以很容易将圆上任意三点分开，那么$d_{vc}=3$。如果是如下图第二种情况时，这条粗线无论如何都不能将圆上的任一三点全完分开，因为圆上必然至少存在两个点的距离小于根号3，那么其对应的$d_{vc}<3$

根据相关理论可以证明，在d维空间中，当数据点分布在半径为R的超球体中，$d_{vc}(A_{\rho })$满足下面的关系$d_{vc}(A_{\rho })\le d+1$

总结一下，这一讲主要学习了线性硬间隔指支持向量机，通过公式的推导，得出了我们的目标表达式和条件，指出了可以使用解二次规划问题的方法求解；接着又学习它背后的理论依据