李宏毅机器学习PTT的理解（2）深度学习为甚深？

在深度学习中，是不是我们模型的隐藏层越多，每一层的单元越多就越好呢？下面我们可以看一下在不同形式的层下的性能

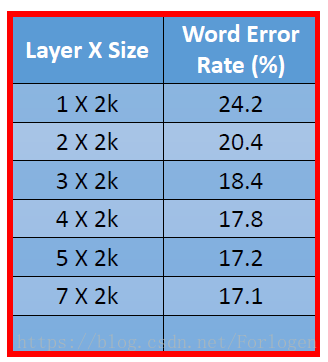
结果是的！这是在我们不考虑其他的因素的情况下的理想情况，现实中可能不能无限制的构建非常非常大的模型。
那么我们能否只设置一个隐藏层，而在这一层设置非常多的神经元，构建一个Fat的神经网络呢？

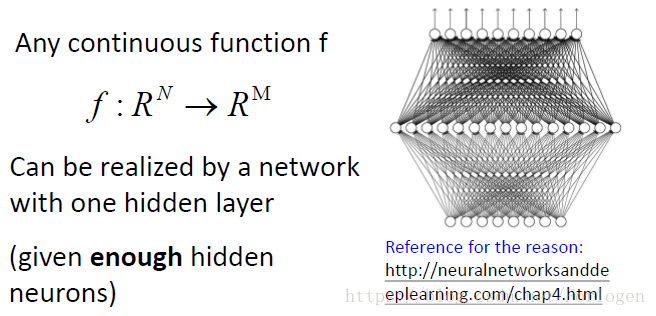
层数不多，每一层很大的网络相比于层数很多每一层不大的网络，哪个更好呢？

我们同样看一下实验的结果

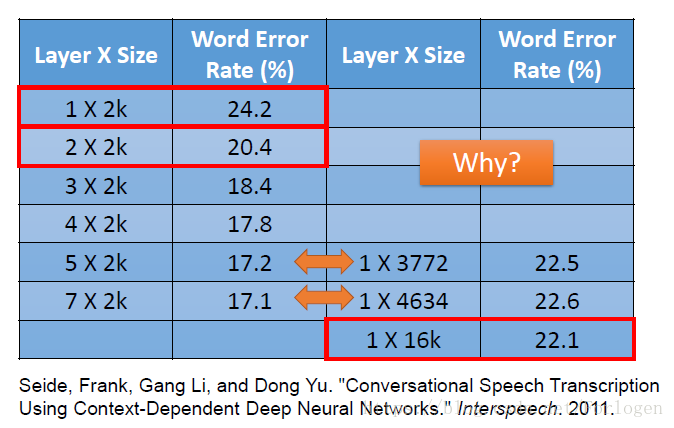
从图中我们可以看出，在每一层的大小相同的情况下，我们的层数越多，性能越好。我们看最后两行，可以看出Fate网络的性能明显差于Thin网络。
那么模型是如何训练的呢？

机器学习的的通用工作流程：定义问题收集数据集、选择衡量成功的指标、确定评估方法、准备数据、开发模型、模型正则化和调节超参数。

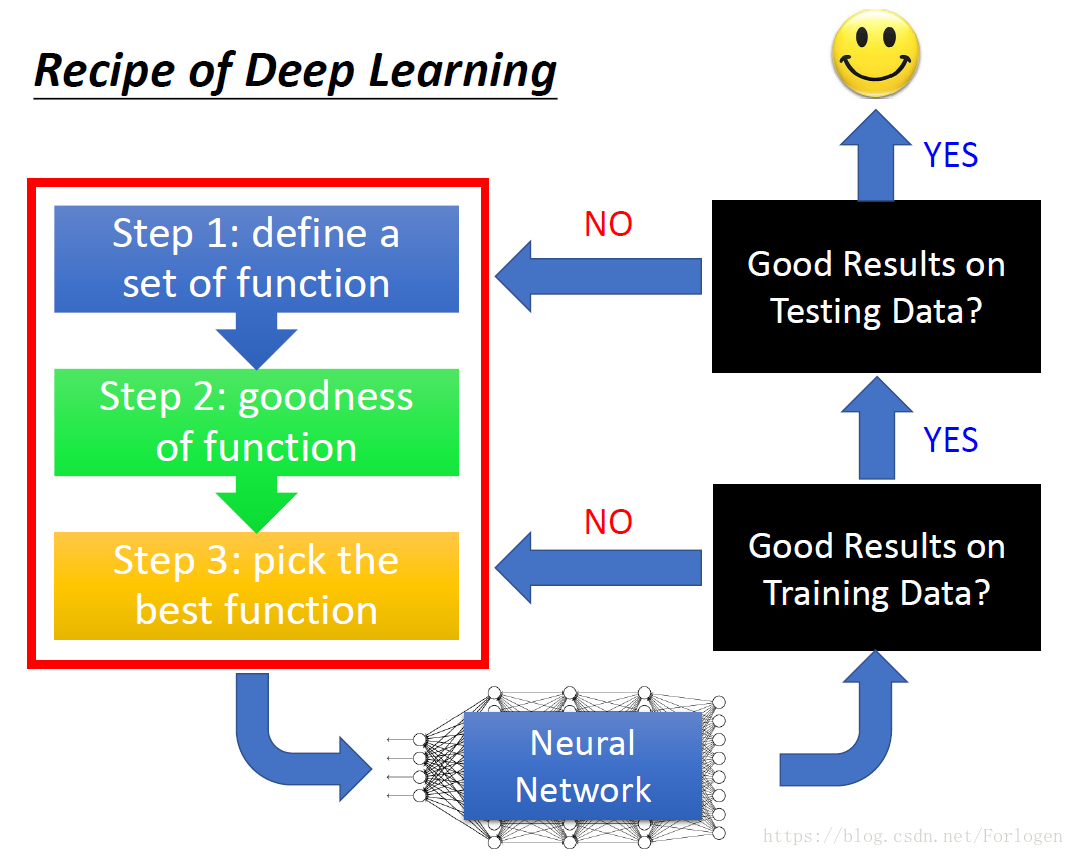
CNN模型在图像分类中的一般构建：

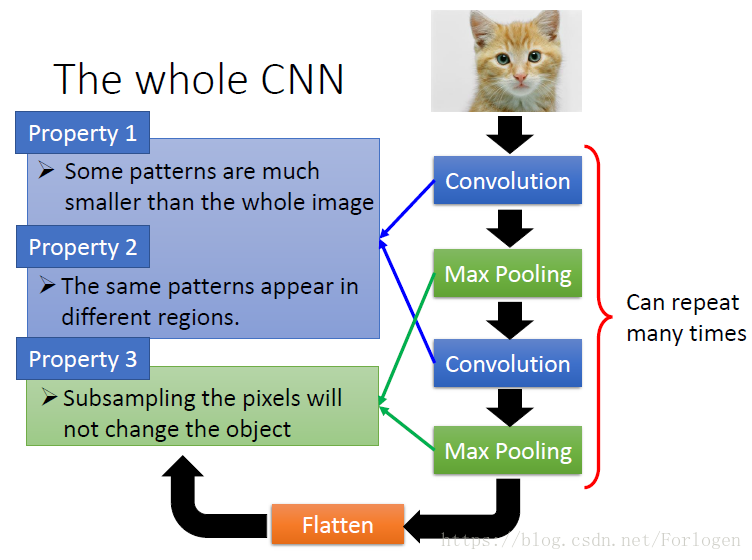
CNN中的卷积运算：

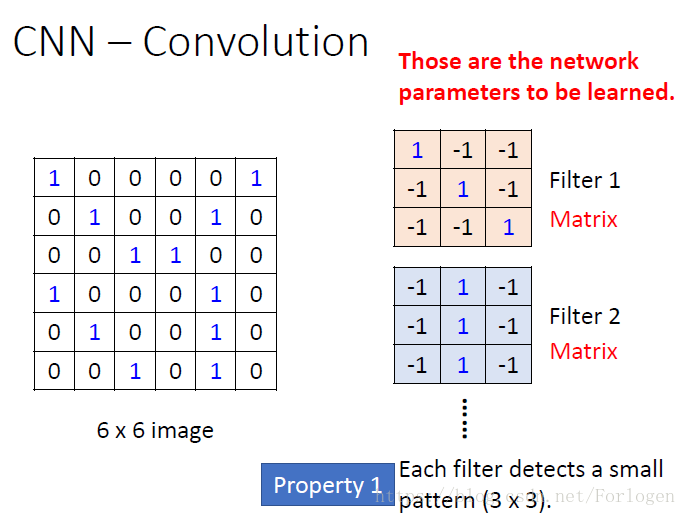
这里假设我们的图像大小为66，我们存在不同的过滤器来对图像进行采用，进行卷积运算，提取某些特定的特征，不同的过滤器就是一个个的矩阵，这里的大小为33

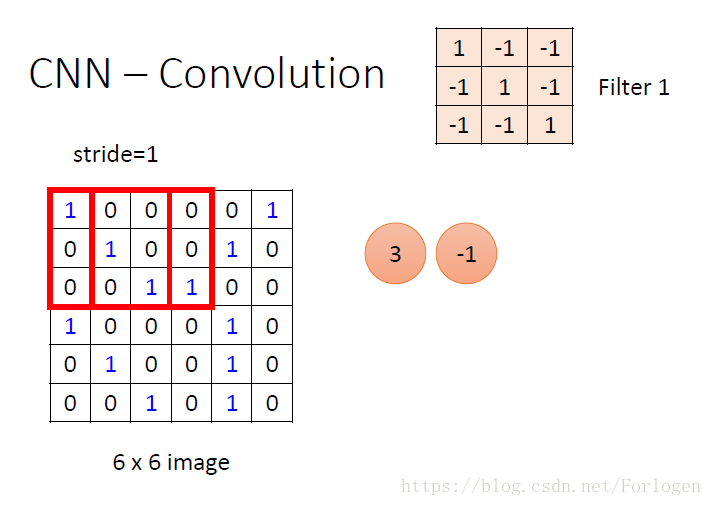
窗口从左到右，从上到下逐步采样，例如第一个窗口的数据为

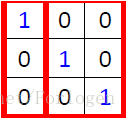
将它和Filter1做卷积元素：11+0-1+0*-1+0*-1+11+0-1+1*-1+0*-1+1+1=3，也就是上图框中的数字，不断的滑动窗口，不断地做卷积运算就可以得到一个特征图。

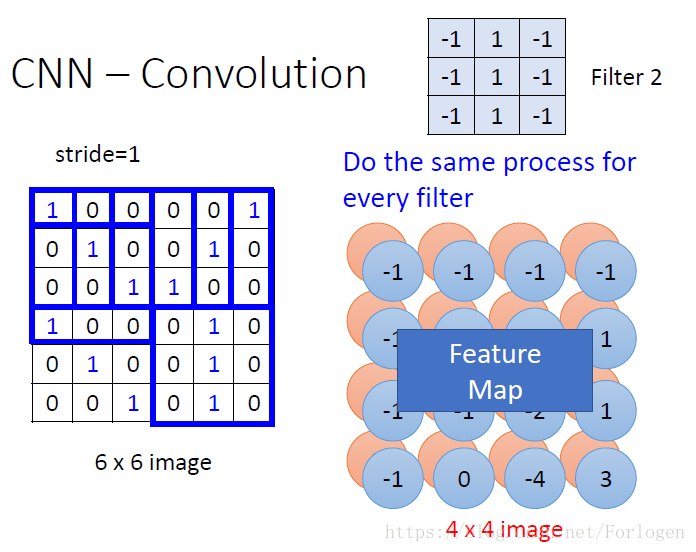
这里我们做了两次卷积，既可以得到这样一个两层的特征图。

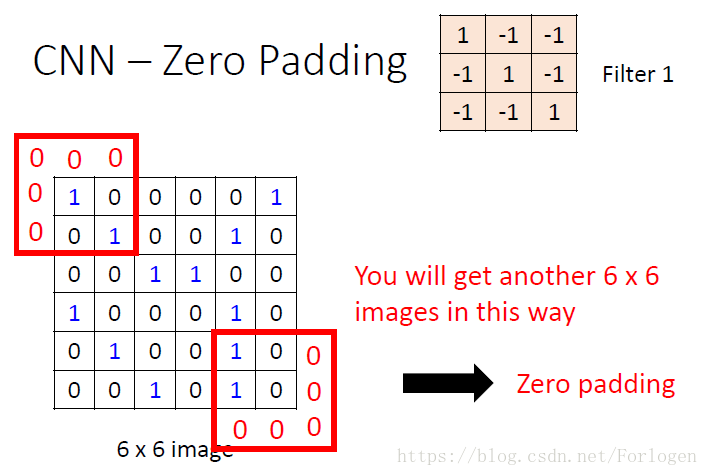
当我们以设置好的窗口滑动时，有时我们无法包含到所有的元素，就需要我们进行填充，如下时零填充：

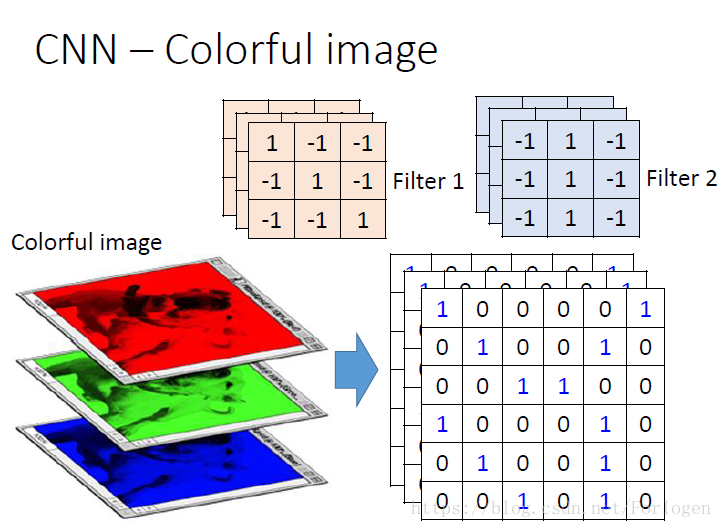
对于彩色图像来说，就有RGB三个通道，这时我们的过滤器的形式也要改变，适应数据，例如下图所示，这里的过滤器是333，得到的特征图为663.

在CNN的一般模型图中，我们可以看到一个Max Pooling的东西，它是什么东西呢？我们来看下图：假设在经过两次卷积运算后得到如下的两个特征图

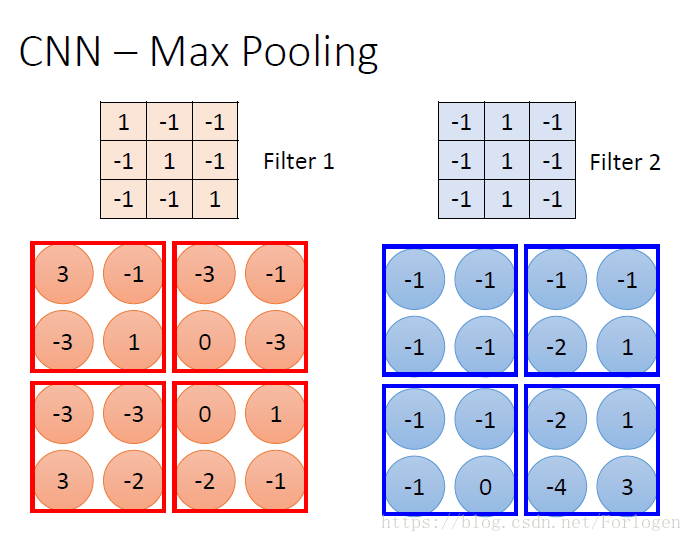
最大池化就是选择窗口中的最大值组成一个更小的特征图，比如我们选择Filter2，经过卷积、最大池化，我们就可以得到如下的特征图：

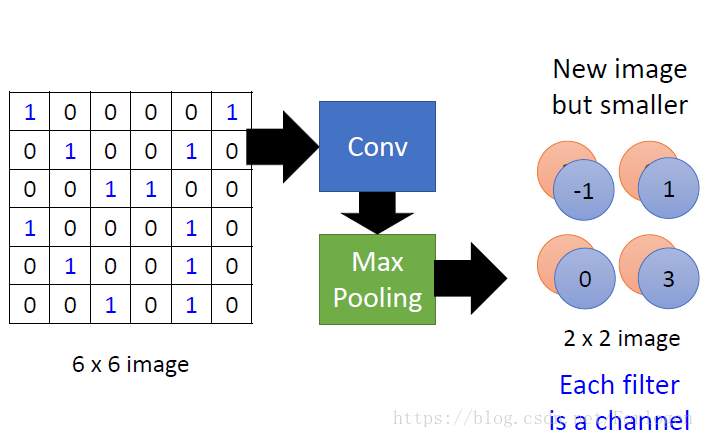
44的就变成了22，这样的新图像表示更小，更易训练，最大池化通道的数量就是过滤器的数量。我们的模型就相当于：


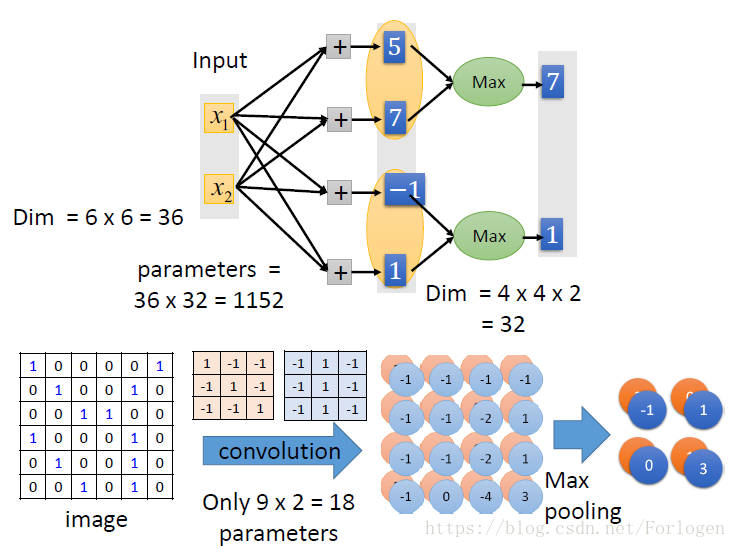
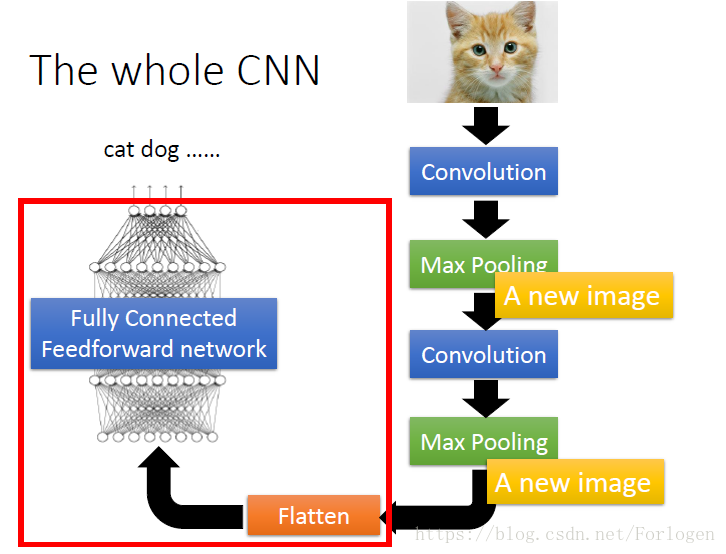
在最后的分类前，需要进行扁平化数据：

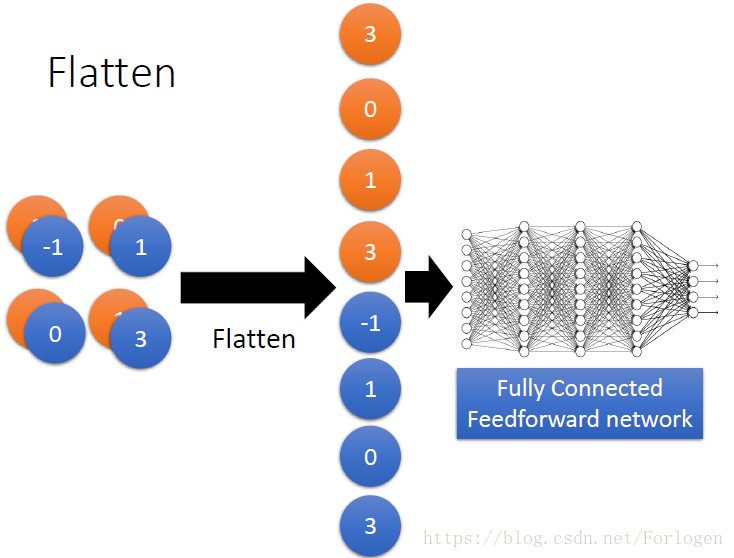
我们传统的神经网络通常就是这样的：

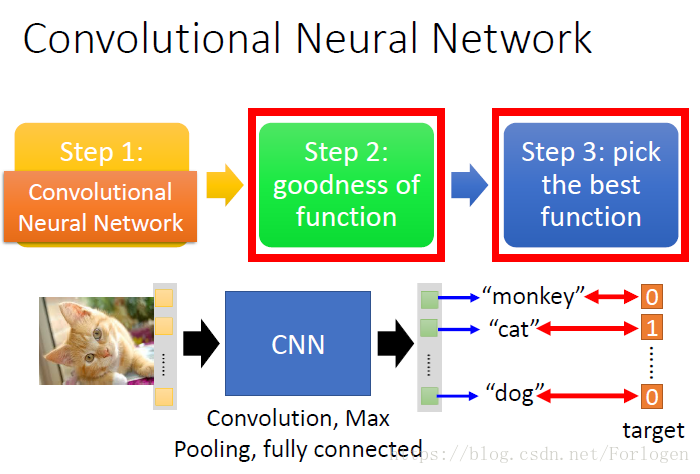
输入图像数据，经过卷积网络和密集连接网络输入分类的结果，其中并没有什么特殊的，只是梯度下降。