Stanford机器学习-降维

一、降维动机：数据压缩

在前面学习了第一个无监督的学习算法-聚类，主要是K-means算法，接下来要学习第二个无监督的算法-降维。促使我们使用降维的原因有很多，可能是我们希望压缩数据，来减小数据占用计算机内存或是硬盘的大小，也可能是希望通过降低数据的维度来加快我们的算法的运行。

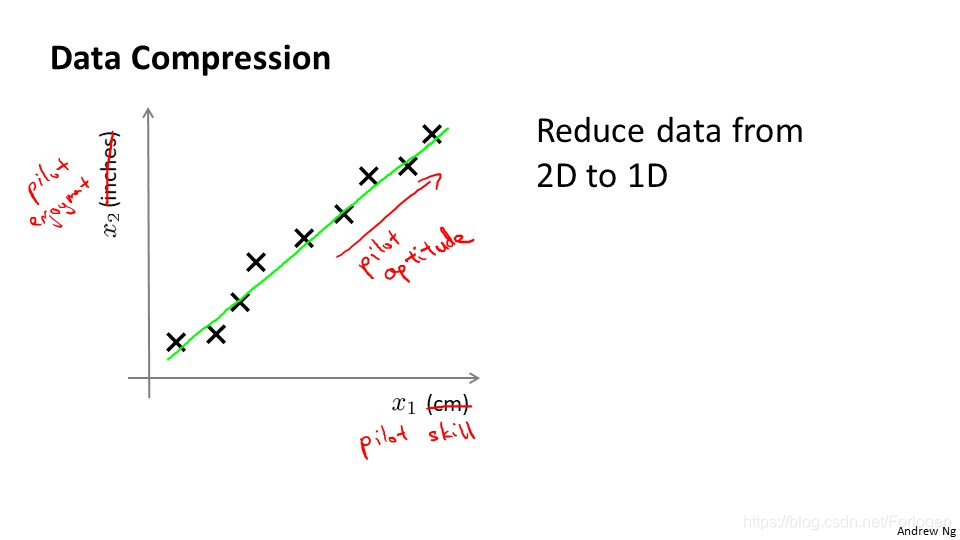
比如我们有上面的一些数据，我们用x1表示长度，单位选择厘米，x2用英寸来表示高度，这样看来两个变量表示的实际意义是一样的，因此我们希望将这个二维的数据降到一维，这样更便于我们的处理。在实际的工程中，我们经常会遇到数据中特征意义冗余的情况，这时降维就显得很重要了。

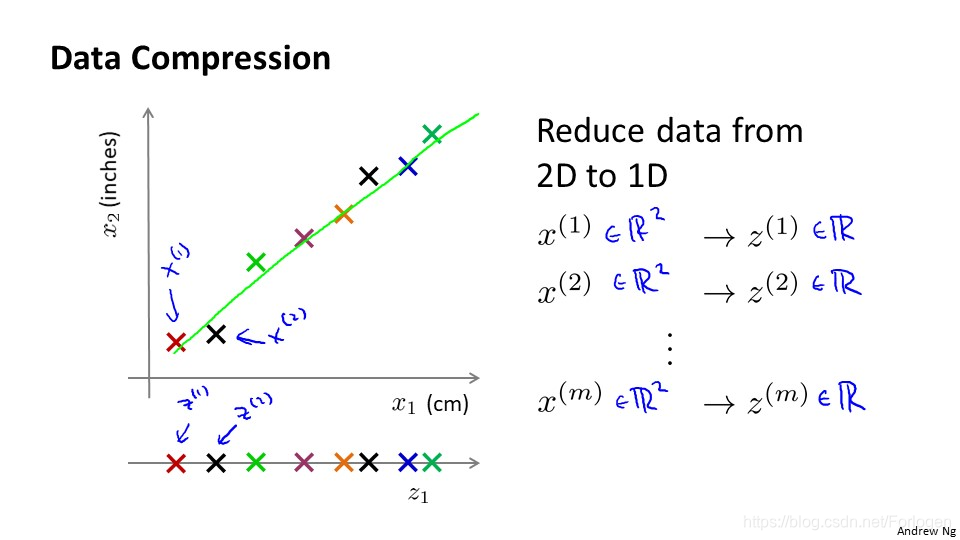
那我们具体怎么样来做呢？我们仍然使用上面的例子，我们用不同的颜色的点表示不同的数据，x(1)表示出的数据，它是一个2维的向量，我们通过降维将其用1维数据Z(i)表示。

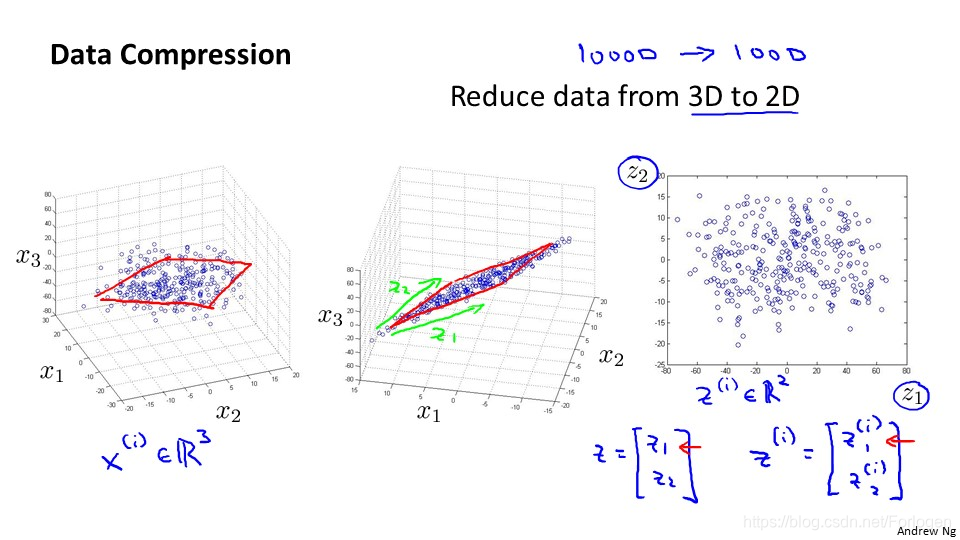
在2维数据上我们可以将其降到1维，即找到一个向量u1,将数据投影到一条直线上；那么在三维上我们要找到两个向量u1和u2，两个方向向量组成一个投影平面，我们将数据投影到这个平面上，就实现了三维到二维的降维，（x1，x2，x3）表示的数据将可以使用(z1，z2)表示。

二、降维动机：数数据可视化

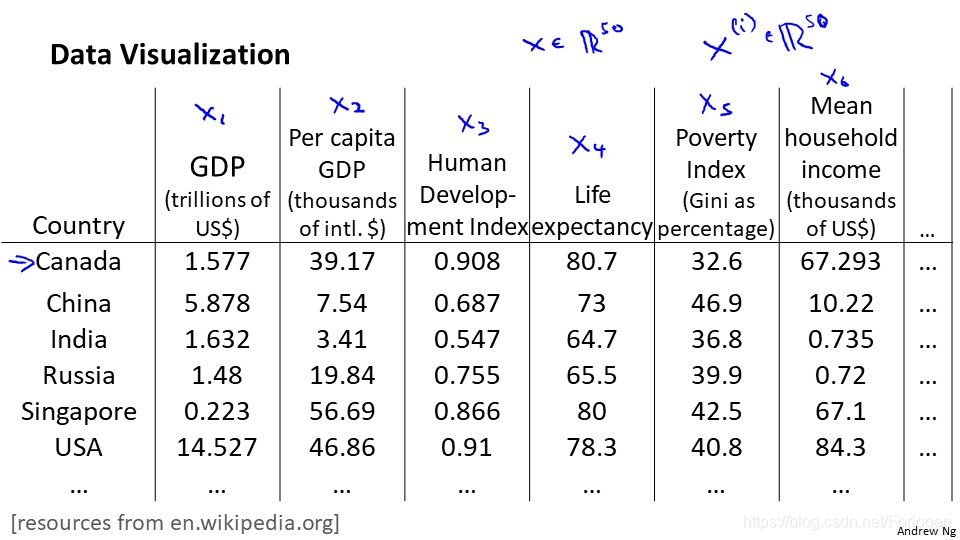
上面我们提到的数据最多也只有三维，但假如我们的数据是上面的：它表示了不同国家的不同指标的数据，对于某一个国家来说，相关的特征就可能有很多个，假设有50个，那么每一条数据都是一个50维的向量，在我们现在的知识下，将50维的数据进行可视化，显然是不可能的，所以我们需要进行降维。

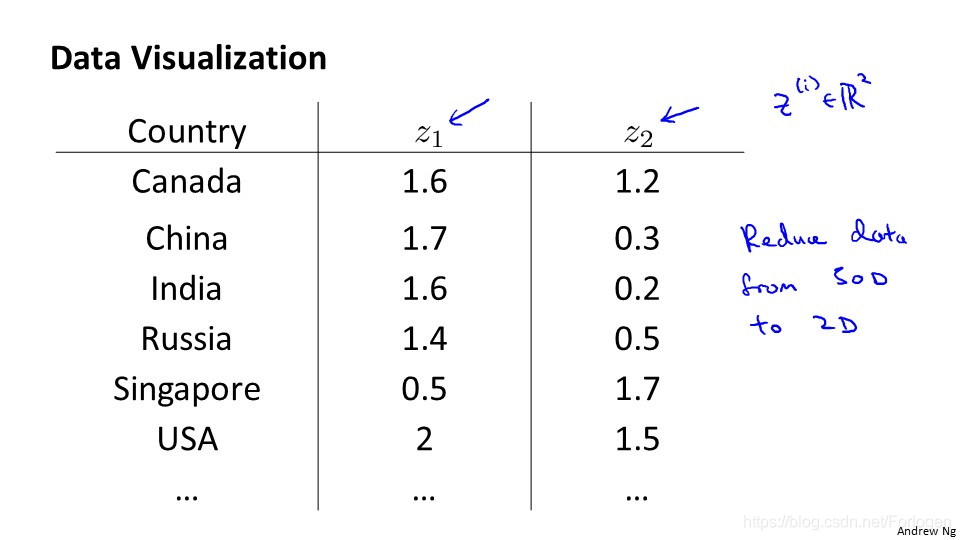
假如我们可以通过算法将其降到2维平面上，分别用z1和z2表示某一国家的特征数据，我们进行可视化就可以得到如下的图。

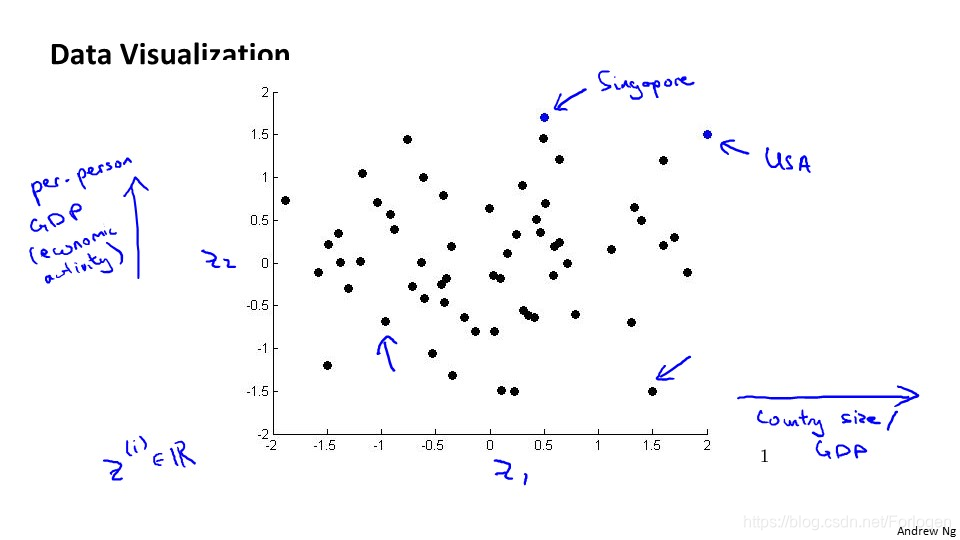
在二维图中，Z1和Z2就表示不同的特征，而坐标图上的点就可以表示具体的某一国家。通过降维我们降低了数据的维数，但是新产生特征的具体意义需要我们来重新定义。

三、主成分分析问题

在降维中，我们最常用的一个算法就是PCA，即主成分分析。

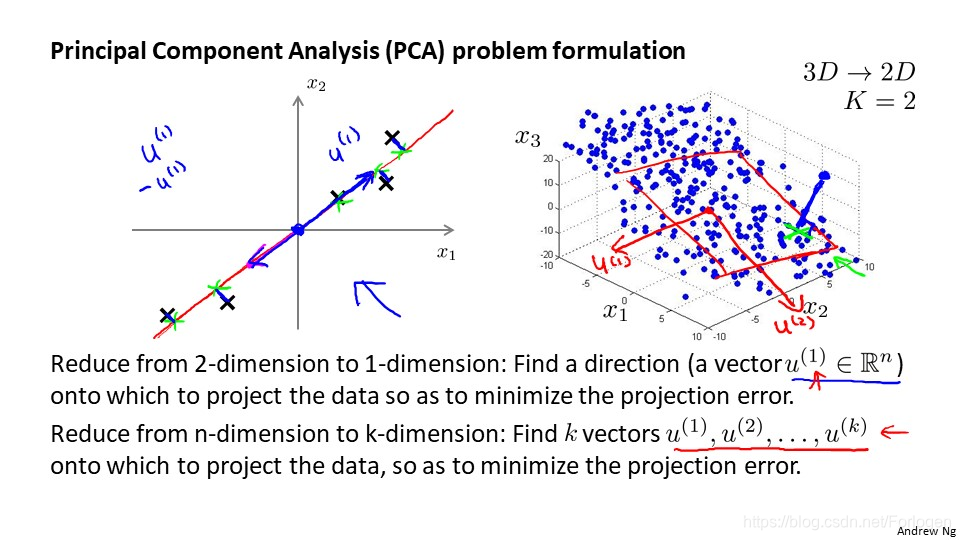
比如在二维数据上，我们希望找到一个方向向量，如品红色线所示的那样，使得数据点投影到向量上时，投影的平均均方误差最小。方向向量在这里是一条经过原点的直线，投影误差就是数据点到直线的垂直距离。而在三维数据上，我们找到的是一个投影平面，我们希望做的仍然是数据点到平面的投影误差的均方误差最小。

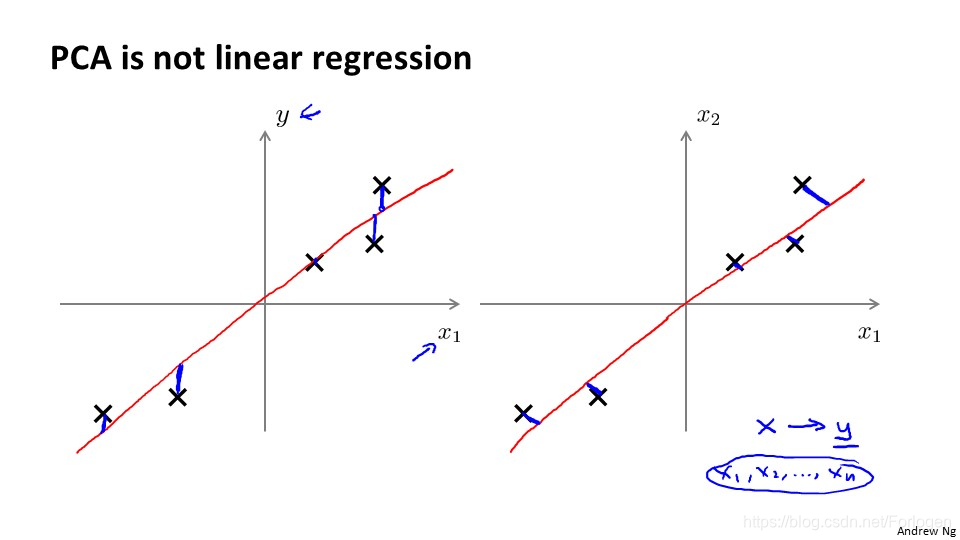
在二维数据上看起来PCA好像和之前的线性回归很像，但是实际它们两个是完全不同的算法。在线性回归中，我们希望得到一个预测结果，减小预测误差，而在PCA中我们不做任何预测，减小的是投影误差。

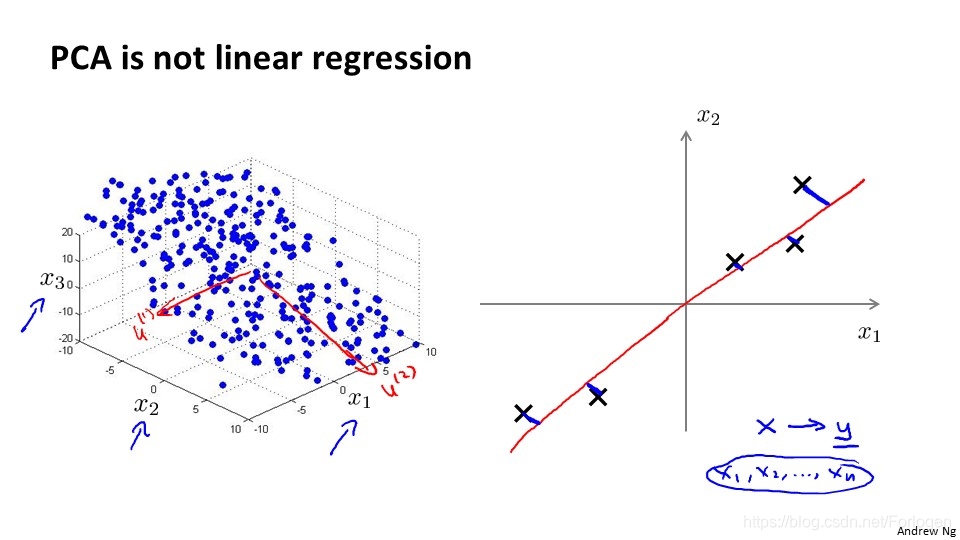
PCA将n个特征降维到K个，就可以用来进行数据压缩，比如我们将100维的数据降到10维时，我们数据的压缩率就达到了90%，但PCA还要保证降维后，数据特性的损失最小。PCA的一个好处就是对数据进行降维后，我们可以对新求出的主元向量的重要性进行排序，根据我们的需要选择最重要的部分，舍弃后面的部分，从而可以达到降维来简化模型，来实现对数据的压缩，同时又保留原有数据的信息，此外还完全无参数限制。在计算过程中，我们完全不需要人为的设定参数或是对计算干预，最后结果只与数据有关，与用户独立。

四、PCA算法

在使用PCA算法进行降维时，首先我们要进行数据的预处理。

对于训练数据，我们进行如下操作：
1. 均值归一化：我们要计算出所有特征的均值，然后令xj= xj -μ。如果特征的取值范围相差较大，我们还需要将其除以标准差σ2。
2. 计算协方差矩阵Σ（不要和求和符号混淆）：
3. 计算协方差矩阵Σ的特征向量，在octave中使用奇异值分解求解）来求解[U, S, V]= svd(sigma)

然后选择前K个向量作为我们降维后的结果，这样我们就得到了一个nk 的矩阵，我们用Ureduce表示，然后用下面的公式计算Z(i)：

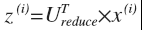
Ureduce的转置是kn的，而x是n1的，所以我们的结果就是k1的。

五、从压缩数据中重构

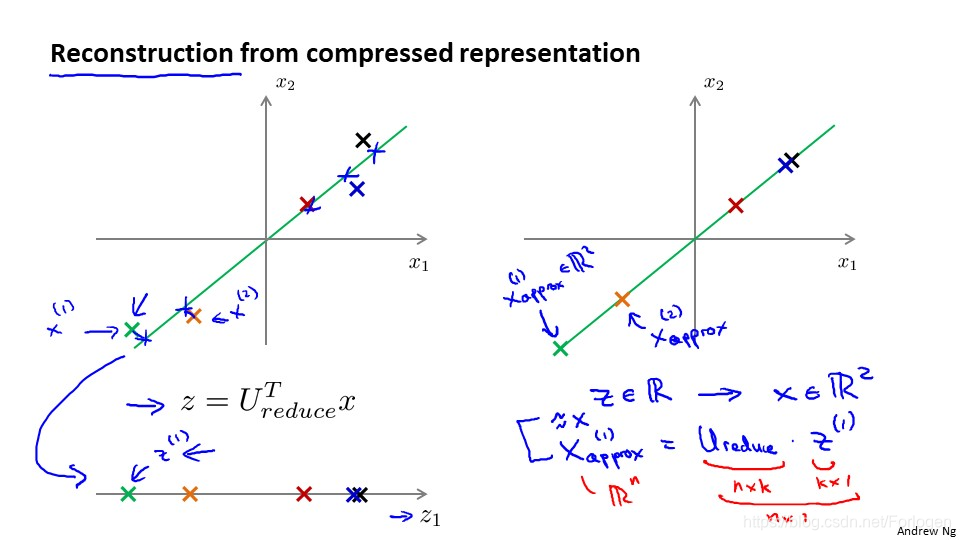
在压缩数据后，我们可以将1000维的数据压缩到10维或是三维到二维等，那么如何回到原来的数据呢？在之前的压缩过程中，我们假设x是2维的，z是1维的，我们使用的方程是：

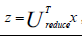
那么相反的对应的方程就是：

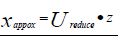
得到的结果是近似于原数据的。

六、选择主成分的数量

那么我们如何选择主成分的数量K呢？

在PCA中我们要减少投影的平均均方误差，而训练集的方差为

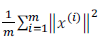
要在均方误差和训练集方差的比例尽可能小的情况下，选择K的最小值，这样我们就可以用到上图所示的公式。如果我们希望他的比例小于1%，那么意味着原本数据99%的方差保留了下来，如果选择保留95% 的偏差，就可以显著的降低数据的维度。

我们需要做的就是使K从1开始不断增加，使用K进行主成分分析，然后看是否满足设定的条件，而条件满足的最小的K就是我们需要的结果。在Octave中我们可以使用下面的公式表示平均均方误差和训练集方差的比例：

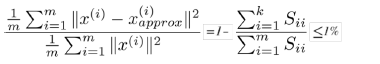
对应的也就是：

其中上面是S矩阵对面线前K个元素的和，下面是对角线所有元素的和。

七、应用PCA的建议

假设我们对一张100*100像素的图片进行计算机视觉的学习，那么就会有1000000个特征，那么我们如何使用PCA呢？一般有如下的步骤：

1. 第一步是运用PCA进行降维到1000
2. 在训练集上运行学习算法
3. 在预测时，采用学习到的Ureduce将其转换成z，再进行预测。

有些人将PCA作为解决过拟合的一种手段，其实是不合适的，还不如进行归一化处理。因为我们在进行主成分分析时只是近似的丢弃掉一些特征，并不会考虑与结果相关的东西，因此可能会丢弃重要的特征，而均一化就不会有出现这样的后果。此外它也不应是在所有的问题中必须使用，只有当我们原始的数据解决不了问题时，就可以使用它来帮助我们解决问题。