动态规划之最长公共子序列

最长公共子序列（LCS）算是动态规划里面的一个经典问题的。本文主要讲LCS的编程实现（python版本）。
LCS问题：给定两个序列$X=<x_1,x_2,...,x_m>$和$Y=<y_1,y_2,...,y_n>$，求X和Y最长的公共子序列。

根据LCS问题的最优子结构，我们可以得到如下公式：

$$c[i,j] = \begin{cases} 0, & \text{if $i=0$ or $j=0$ } \\[2ex] c[i-1,j-1] , & \text{if $i,j>0$ and $x_i=y_j$} \\[2ex] max(c[i,j-1],c[i-1,j]) , & \text{if $i,j>0$ and $x_i\neq y_j$} \end{cases}$$
序列的生成过程如下图：

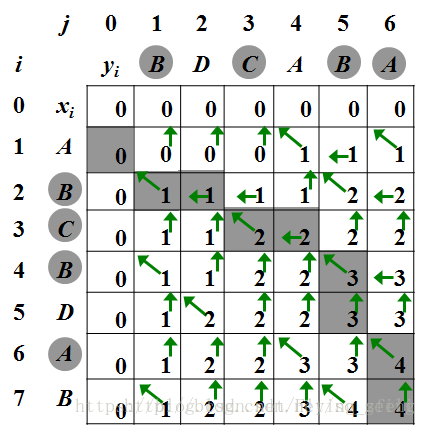
编程实现：
一 保存两个矩阵s,d：s保存子序列结果，d保存共同字符信息，非必须：

class Solution:
    def LCS(self, L1, L2):
        s = [[0 for i in range(len(L1)+1)] for j in range(len(L2)+1)]
        d = [[0 for i in range(len(L1)+1)] for j in range(len(L2)+1)]
        for i, l2 in enumerate(L2):
            for j, l1 in enumerate(L1):
                if l1 == l2:
                    s[i+1][j+1] = s[i][j] + 1
                    d[i+1][j+1] = 3
                elif l1 != l2:
                    if s[i+1][j] > s[i][j+1]:
                        s[i + 1][j + 1] = s[i+1][j]
                        d[i + 1][j + 1] = 1
                    else:
                        s[i + 1][j + 1] = s[i][j+1]
                        d[i + 1][j + 1] = 2
        return s, d

    def reSeq(self, d, m, n, L1, s):
        if s[m][n] == 0:
            return 0
        # if d[m][n] > d[m][n-1] and d[m][n] > d[m-1][n]:
        if d[m][n] == 3:
            self.reSeq(d, m-1, n-1, L1, s)
            print (L1[n-1])
        elif d[m][n] == 2:
            self.reSeq(d, m-1, n, L1, s)
        elif d[m][n] == 1:
            self.reSeq(d, m, n-1, L1, s)

if __name__ == "__main__":
    L1 = ['B', 'D', 'C', 'A', 'B', 'A']
    L2 = ['A', 'B', 'C', 'B', 'D', 'A', 'B']
    m = len(L2)
    n = len(L1)
    R = Solution()
    s, d = R.LCS(L1, L2)
    print ('s:', s)
    print('d:', d)
    R.reSeq(d, m, n, L1, s)

结果如下：

s: [[0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 1, 1], [0, 1, 1, 1, 1, 2, 2], [0, 1, 1, 2, 2, 2, 2], [0, 1, 1, 2, 2, 3, 3], [0, 1, 2, 2, 2, 3, 3], [0, 1, 2, 2, 3, 3, 4], [0, 1, 2, 2, 3, 4, 4]]
d: [[0, 0, 0, 0, 0, 0, 0], [0, 2, 2, 2, 3, 1, 3], [0, 3, 1, 1, 2, 3, 1], [0, 2, 2, 3, 1, 2, 2], [0, 3, 2, 2, 2, 3, 1], [0, 2, 3, 2, 2, 2, 2], [0, 2, 2, 2, 3, 2, 3], [0, 3, 2, 2, 2, 3, 2]]
B
C
B
A

二 保存矩阵s：s保存子序列结果，不再维护d矩阵，节省内存开销：

class Solution:
    def LCS(self, L1, L2):
        s = [[0 for i in range(len(L1)+1)] for i in range(len(L2)+1)]
        for i, l2 in enumerate(L2):
            for j, l1 in enumerate(L1):
                if l1 == l2:
                    s[i+1][j+1] = s[i][j] + 1
                else:
                    s[i + 1][j + 1] = max(s[i+1][j], s[i][j+1])
        return s

    def reSeq(self, m, n, L1, s):
        if s[m][n] == 0:
            return 0
        if s[m][n] > s[m][n-1] and s[m][n] > s[m-1][n]:
            self.reSeq(m - 1, n - 1, L1, s)
            print(L1[n - 1])
        elif s[m][n-1] > s[m-1][n]:
            self.reSeq(m, n - 1, L1, s)
        else:
            self.reSeq(m-1, n, L1, s)

if __name__ == "__main__":
    L1 = ['B','D','C','A','B','A']
    L2 = ['A','B', 'C', 'B','D', 'A', 'B']
    m = len(L2)
    n = len(L1)
    R = Solution()
    s = R.LCS(L1, L2)
    print ('s:', s)
    R.reSeq(m, n, L1, s)

结果如下：

s: [[0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 1, 1], [0, 1, 1, 1, 1, 2, 2], [0, 1, 1, 2, 2, 2, 2], [0, 1, 1, 2, 2, 3, 3], [0, 1, 2, 2, 2, 3, 3], [0, 1, 2, 2, 3, 3, 4], [0, 1, 2, 2, 3, 4, 4]]
B
C
B
A

参考：《算法导论》
算法导论—–最长公共子序列LCS（动态规划）