491. Non-decreasing Subsequences 46. Permutations 47. Permutations II-优快云博客

本文链接：https://blog.youkuaiyun.com/Fai_B/article/details/134409854

文章讲述了如何使用回溯法解决两个问题：一是生成给定整数数组的非递减子序列（至少包含两个元素），二是处理不包含重复元素的全排列。作者提供了两种解决方案，包括利用集合去重和标记数组元素是否已使用的策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Given an integer array nums, return all the different possible non-decreasing subsequences of the given array with at least two elements. You may return the answer in any order.

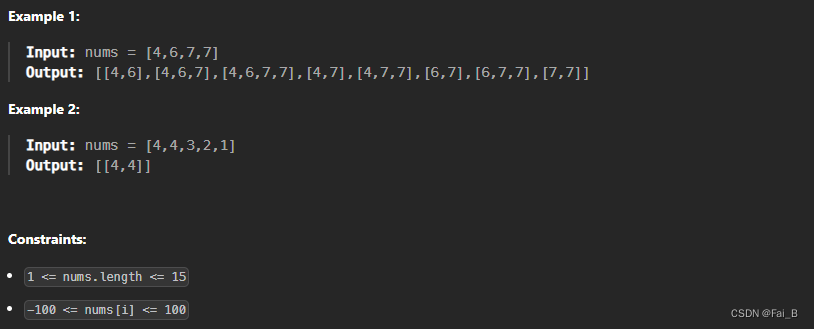
1. each layer de - duplicate: uset = set( ) ...... uset.add(nums[i]) / like one_path

2. if (path and nums[i] < path[-1]) or nums[i] in uset().......continue

backtracking + recursion:

class Solution:
    def findSubsequences(self, nums: List[int]) -> List[List[int]]:
        result = []
        self.backtracking(nums, [], result, 0)
        return result
    
    def backtracking(self, nums, path, result, startindex):
        if len(path) > 1:
            result.append(path[:])

        uset = set() #each layer de-duplicate
        for i in range(startindex, len(nums)):    
            if (path and nums[i] < path[-1]) or nums[i] in uset: # wrong: nums[i] <= nums[i-1] [7,7]可以
                continue
            
            uset.add(nums[i])
            path.append(nums[i]) 
            self.backtracking(nums, path, result, i+1)
            path.pop()

46. Permutations 全排列

Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.

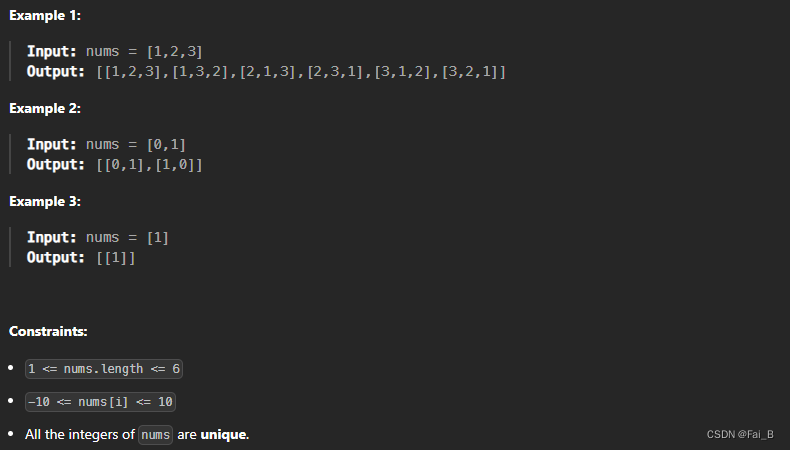
no index or start_index:

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        result = []
        self.backtracking(nums, [], result)
        return result
    
    def backtracking(self, nums, path, result):
        if path and len(path) == len(nums):
            result.append(path[:])
            return
        
        for i in range(len(nums)):
            if nums[i] in path: # nums=[0,1]  delete [0,0][1,1] this kind of collection
                continue
            path.append(nums[i])
            self.backtracking(nums, path, result)
            path.pop()

using used[ ]:

class Solution:
    def permute(self, nums):
        result = []
        self.backtracking(nums, [], [False] * len(nums), result)
        return result

    def backtracking(self, nums, path, used, result):
        if len(path) == len(nums):
            result.append(path[:])
            return
        for i in range(len(nums)):
            if used[i]:
                continue
            used[i] = True
            path.append(nums[i])
            self.backtracking(nums, path, used, result)
            path.pop()
            used[i] = False

47. Permutations II

Given a collection of numbers, nums, that might contain duplicates, return all possible unique permutations in any order.

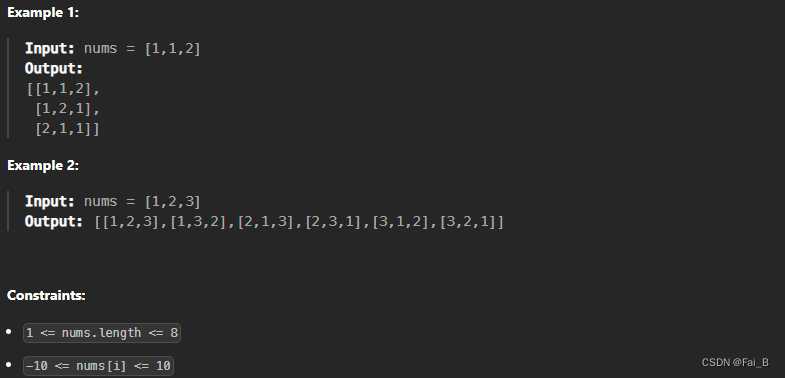
1. do not use ~~path not in result~~ :

2. used = [False] * len(nums)

3.solving Duplicate paths: nums.sort()

i>0 and nums[i] == nums [i-1] and used[i-1] ...... continue

4. Each number can only be used once in one path: used[i] ........continue

class Solution:
    def permuteUnique(self, nums):
        nums.sort()  # 排序
        result = []
        self.backtracking(nums, [], [False] * len(nums), result)
        return result

    def backtracking(self, nums, path, used, result):
        if len(path) == len(nums):
            result.append(path[:])
            return
        for i in range(len(nums)):
            if (i > 0 and nums[i] == nums[i - 1] and not used[i - 1]) or used[i]:
                continue
            used[i] = True
            path.append(nums[i])
            self.backtracking(nums, path, used, result)
            path.pop()
            used[i] = False