216. Combination Sum III 17. Letter Combinations of a Phone Number

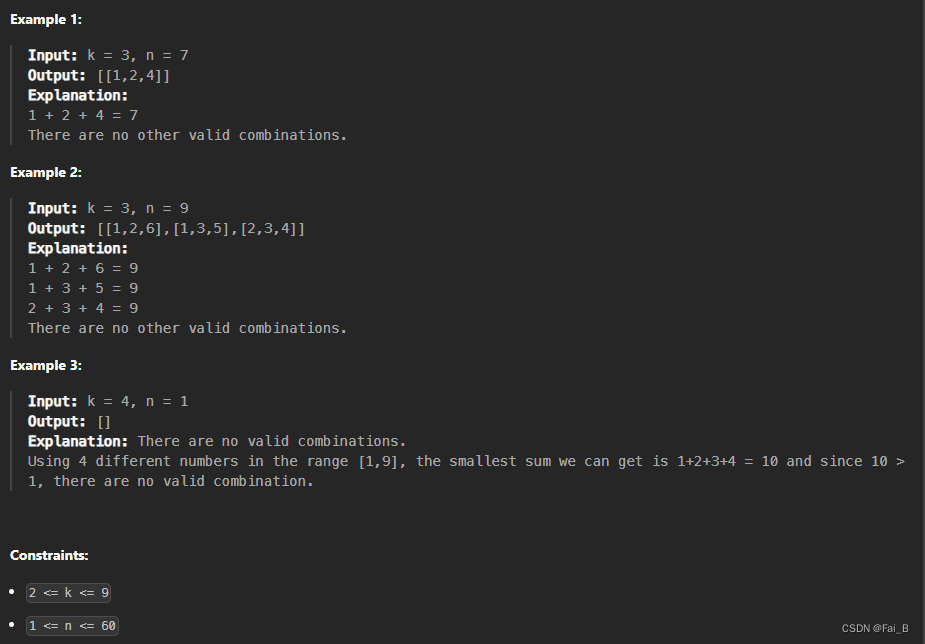
Find all valid combinations of k numbers that sum up to n such that the following conditions are true:

• Only numbers 1 through 9 are used.
• Each number is used at most once.

Return a list of all possible valid combinations. The list must not contain the same combination twice, and the combinations may be returned in any order.

 my solution:

class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        result =[]
        self.backtracking(k, n, [], result, 1)
        return result

    
    def backtracking(self, k, n, path, result, startindex):
        if sum(path) == n and len(path) == k:
            result.append(path[:])
            return
        
        for i in range(startindex, 10): # 超时 (startindex, 10 - (k-len(path)) + 1) ；因为sum 大于 target时候 没跳出循环，len会不断变大，for循环就是负数了
            path.append(i)
            self.backtracking(k, n, path, result, i+1)
            path.pop()

There is also a important pruning剪枝 place, when the number of individuals is not exceeded but the total number is exceeded, it returns directly 

solution after pruning：

class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        result =[]
        self.backtracking(k, n, [], result, 1)
        return result

    
    def backtracking(self, k, n, path, result, startindex):
        if sum(path) > n: # for剪枝的要求
            return

        if sum(path) == n and len(path) == k:
            result.append(path[:])
            return
        
        for i in range(startindex, 10 - (k-len(path)) + 1): #剪枝后
            path.append(i)
            self.backtracking(k, n, path, result, i+1)
            path.pop()

standard solution：

class Solution:
    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        result = []  # 存放结果集
        self.backtracking(n, k, 0, 1, [], result)
        return result

    def backtracking(self, targetSum, k, currentSum, startIndex, path, result):
        if currentSum > targetSum:  # 剪枝操作
            return  # 如果path的长度等于k但currentSum不等于targetSum，则直接返回
        if len(path) == k:
            if currentSum == targetSum:
                result.append(path[:])
            return
        for i in range(startIndex, 9 - (k - len(path)) + 2):  # 剪枝
            currentSum += i  # 处理
            path.append(i)  # 处理
            self.backtracking(targetSum, k, currentSum, i + 1, path, result)  # 注意i+1调整startIndex
            currentSum -= i  # 回溯
            path.pop()  # 回溯

17. Letter Combinations of a Phone Number

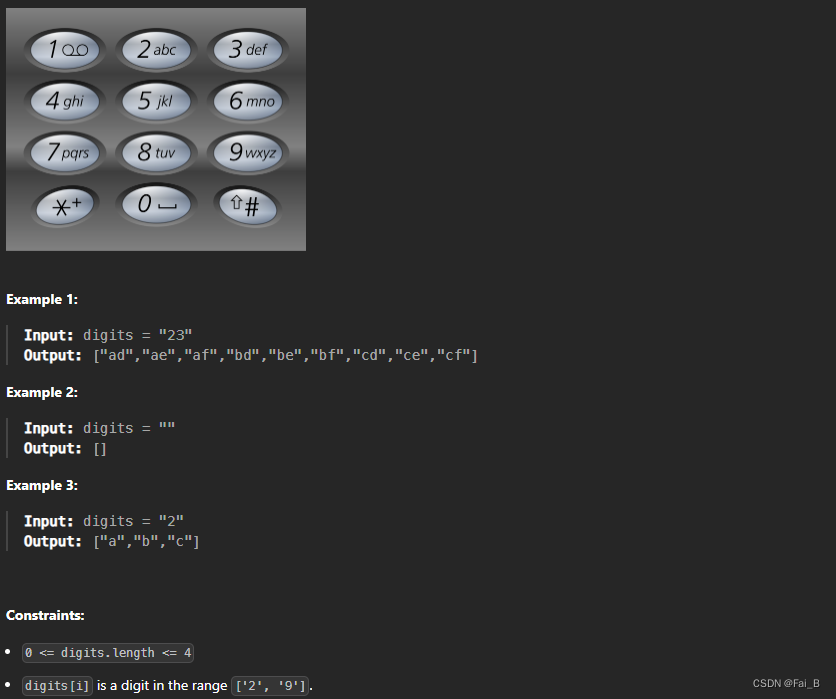
Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent. Return the answer in any order.

A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.

 def init : self. lettermap = [ ],    self. result = [ ] ,     self.s =""

index: digits的index ：Depth of the tree

backtracking:

class Solution:
    def __init__(self):
        self.s = ""
        self.result = []
        self.map =[
        "", #0
        "", #1
        "abc",#2
        "def",
        "ghi",
        "jkl",
        "mno",
        "pqrs",
        "tuv",
        "wxyz"
        ]
    
    def backtracking(self, digits, index):
        if len(self.s) == len(digits): # if index == len(digits)
            self.result.append(self.s)
            return # 这个return一定不能掉 ，下面的self.backtracking满足这个条件就直接执行 self.s = self.s[:-1]
        digit = int(digits[index]) #Convert the number at the index to an integer 
        letters = self.map[digit]  # Get the corresponding character set “abc”....
        for letter in letters:
            self.s += letter
            self.backtracking(digits, index+1)
            self.s = self.s[:-1] #Backtrack to remove the last added character 

    def letterCombinations(self, digits: str) -> List[str]:
        if len(digits) == 0:
            return self.result
        self.backtracking(digits, 0)
        return self.result