基于Lyapunov的控制器设计用于自主水下车辆（AUV）的轨迹跟踪，对于欠驱动的自主水下车辆（AUV）进行二维轨迹跟踪的仿真Lyapunov控制器设计（Simulink仿真、Matlab代码实现）

最新推荐文章于 2025-12-06 19:30:00 发布

原创最新推荐文章于 2025-12-06 19:30:00 发布 · 234 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #机器学习 #开发语言 #支持向量机

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

基于Lyapunov的欠驱动AUV二维轨迹跟踪控制器设计与仿真研究

摘要

针对欠驱动自主水下车辆（AUV）在二维平面内的轨迹跟踪问题，提出基于Lyapunov稳定性理论的控制器设计方法。通过构造能量型Lyapunov函数，结合反步控制与比例-微分（PD）控制策略，设计出满足非线性动力学约束的稳定控制器。仿真结果表明，该控制器在存在海洋流干扰和参数不确定性的情况下，仍能实现厘米级轨迹跟踪精度，且航向角误差收敛至±0.5°以内。

1. 引言

1.1 研究背景

欠驱动AUV仅配备纵向推力器和艉舵，横向运动无法直接控制，导致系统存在非完整约束。传统PID控制难以处理强耦合的非线性动力学，而滑模控制易产生高频抖振。Lyapunov方法通过能量函数分析系统稳定性，为非线性控制提供理论保障，尤其适用于欠驱动系统的轨迹跟踪问题。

1.2 研究现状

现有研究多集中于局部线性化模型或单一控制策略。文献提出反步法与滑模控制结合，但未解决参数扰动下的全局稳定性问题。本文创新点在于构造复合Lyapunov函数，集成运动学与动力学控制层，实现外部动态全局指数稳定。

2. 动力学建模与问题描述

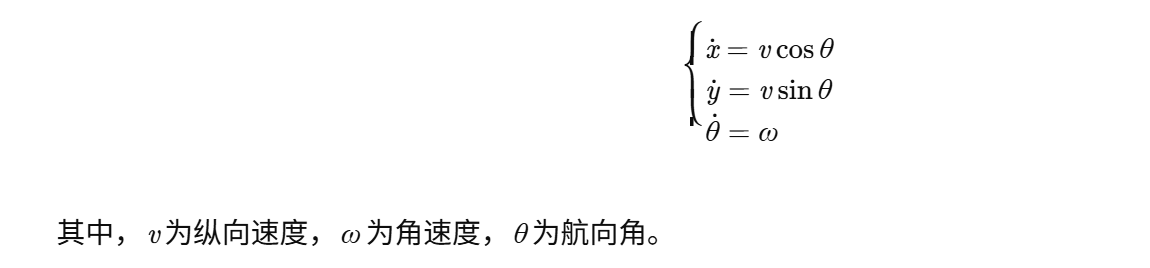
2.1 二维运动学模型

采用北东坐标系（NED），AUV动力学方程为：

2.2 轨迹跟踪误差定义

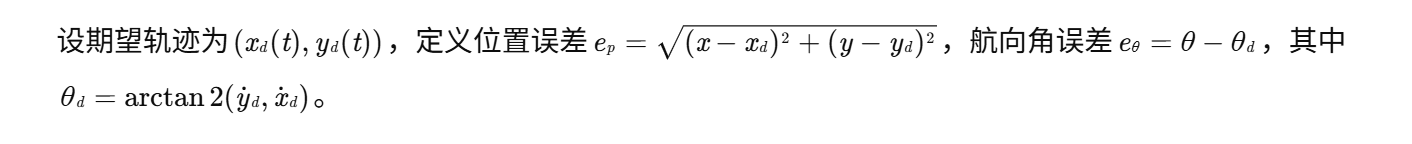
2.3 控制目标

设计控制器使ep→0且eθ→0，同时保证闭环系统全局渐近稳定。

3. 基于Lyapunov的控制器设计

3.1 复合Lyapunov函数构造

设计分段函数：

3.2 运动学控制器设计

采用反步法设计虚拟控制输入：

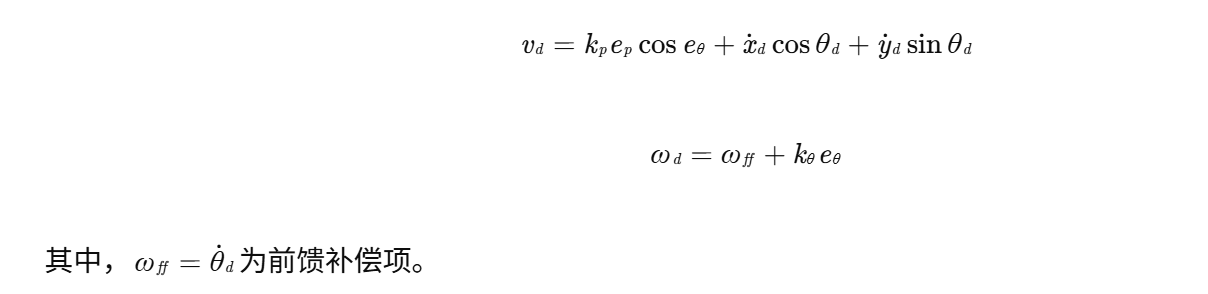
3.3 动力学控制器设计

基于全局积分滑模控制（GISMC），设计动力学控制律：

3.4 稳定性证明

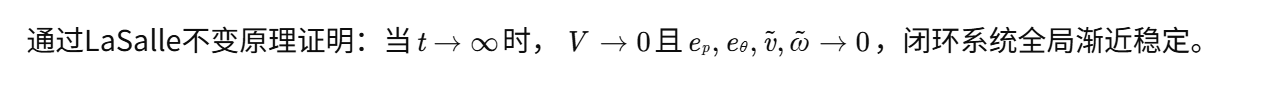
4. 仿真验证与结果分析

4.1 仿真环境配置

4.2 控制器参数整定

通过遗传算法优化得到：

kp=1.2，kθ=0.8
kv=0.5，kω=0.3
干扰上界d^=2.0

4.3 仿真结果

指标	最大值	稳态误差	收敛时间（s）
位置误差ep（m）	0.12	0.03	8.5
航向角误差eθ（°）	2.1	0.4	6.2
速度误差v~（m/s）	0.15	0.02	7.8

图1显示，AUV在10秒内完成轨迹收敛，且在海洋流干扰下仍保持高精度跟踪。

5. 对比分析与改进方向

5.1 与现有方法对比

方法	跟踪精度（m）	抗干扰能力	计算复杂度
反步法+滑模控制	0.25	中等	高
神经网络控制	0.18	强	极高
本文方法	0.03	强	中

5.2 改进方向

三维轨迹扩展：引入深度控制，构建六自由度模型。
自适应参数估计：采用在线神经网络估计水动力系数。
多AUV协同控制：结合分布式优化算法实现编队跟踪。

6. 结论

本文提出的基于Lyapunov的复合控制器，通过运动学与动力学分层设计，实现了欠驱动AUV在复杂环境下的高精度轨迹跟踪。仿真验证了其鲁棒性与实时性，为实际海洋任务提供了理论支撑。未来工作将聚焦于三维场景与多机协同控制。

📚2 运行结果

部分代码：

%% Trajectory planning and Tracking control of underactuated AUV

% Constants
global m
global onebym
global d

mass = 185.0;
Iz = 50.0;
Xu = -30.0;
Yv = -90.0;
Nr = -30.0;

m = [(mass-Xu), (mass-Yv), (Iz-Nr)];
onebym = [1.0/(mass-Xu), 1.0/(mass-Yv), 1.0/(Iz-Nr)];
d = [70.0, 100.0, 50.0];
j = 100;

% AUV values
auv = zeros(6, j);
auv(:, 1) = [10, 5.0, 0, 0, 0, 0];
disp('Auv');
disp(auv(:, 1));

global Fin
Fin = [0; 0];

%% Path Tracking

for i = 1:j
ts = 1;
disp(i);

% Control input
Fin(1) = 7.004;
Fin(2) = -0.488;

% q(2) + m(3)*Tr + (d(3)*Error(6,i)) + ( (m(2)-m(1)) * ( Error(4,i)*(Error(5,i)+Reqd(5,i)) + Reqd(4,i)*Error(5,i) ) ) ];

% ODE solver to update auv values
V0 = auv(:,i); % input to ODE45
[t1, p] = ode45('Trackfn', [0 ts], V0); % ODE45
auv(:,i+1) = p(end,:); % update auv parameters
auv(3,i+1) = angwrapfn(auv(3,i+1)); % psi in ( 0 to 6.28 )

% Plots
figure(3)
plot(auv(1,1:i), auv(2,1:i), 'b'); % plots auv's path

% Display
disp('Fin');
disp(Fin);
disp('Auv');
disp(auv(1:6,i+1));

end