基于改进粒子群优化算法的柔性车间调度问题（Python代码实现）

最新推荐文章于 2025-12-01 22:20:41 发布

原创最新推荐文章于 2025-12-01 22:20:41 发布 · 626 阅读

28 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #python #大数据 #支持向量机

💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

💥1 概述

针对以最大完工时间最小为优化目标的柔性作业车间调度问题(Flexible Job-shop Scheduling Problem,FJSP),采用改进的粒子群算法进行求解。该方法在选择算子时,通过加入轮盘赌策略,增加种群的多样性,提升了算法全局寻优能力。通过与传统粒子群方法进行算例实验对比,改进粒子群算法在全局寻优速度和求最小解方面均优于传统方法。

基于改进粒子群优化算法的柔性车间调度问题研究

一、柔性车间调度问题（FJSP）的定义与特点

柔性车间调度问题（FJSP）是经典作业车间调度问题（JSP）的扩展，其核心在于允许工件的每道工序在多台可选机器上加工，且加工时间可不同。这种柔性特性使其更贴近实际生产场景。FJSP需要同时解决两个子问题：

机器分配：为每道工序选择合适的机器；
工序排序：确定同一机器上各工序的加工顺序。

问题假设与约束条件：

每台机器一次仅加工一道工序；
工件间无优先级关系，工序顺序严格遵循工艺要求；
加工过程不可中断，原料已就绪；
机器故障时需基于最晚加工时间进行重调度。

分类与评价指标：

完全柔性（T-FJSP） 与 部分柔性（P-FJSP） ：P-FJSP更符合实际生产需求。
主要优化目标包括最大完工时间最小化、机器负荷均衡化等。

二、传统粒子群优化算法（PSO）在调度问题中的应用现状

PSO是一种基于群体智能的优化算法，通过模拟鸟群协作行为进行搜索。其优势在于参数少、收敛快、易于实现，适用于实时性要求高的场景。然而，在FJSP中面临以下挑战：

离散化需求：FJSP为组合优化问题，需设计离散编码机制；
局部最优陷阱：传统PSO在高维离散空间中易早熟收敛；
多目标优化：需平衡多个冲突目标（如时间、成本、能耗）。

实际应用案例：

云计算任务调度：改进PSO通过正弦余弦算法增强全局搜索能力，任务处理效率提升54.8%；
微电网调度：多目标PSO（MOPSO）动态调整权重，优化经济性与环境友好性。

三、改进PSO算法的核心方向

为提高PSO在FJSP中的性能，现有研究主要从以下方向改进：

改进方向	具体策略	效果
初始化策略	混沌映射（如Circle映射）生成均匀初始种群	提升种群多样性，避免局部最优
参数动态调整	惯性权重非线性递减、学习因子时变调节	平衡全局搜索与局部开发能力
多种群协作	划分精英子群与普通子群，差异化更新策略	增强信息共享与协同进化
混合算法设计	结合遗传算法（交叉/变异）、禁忌搜索（邻域搜索）	继承PSO的快速收敛性，引入局部精细化搜索
离散化与编码优化	机器负荷平衡初始化、工序保留交叉（POX）、随机点保存交叉（RPX）	适应FJSP的离散特性，提升解的质量与收敛速度

四、针对FJSP的改进PSO策略及效果

离散PSO算法：
- 编码机制：采用双层编码（机器分配+工序顺序），结合机器负荷平衡初始化；
- 更新算子：引入变异、POX交叉（保留工序顺序）、RPX交叉（保留随机点）；
- 实验效果：在Brandimarte数据集上，最大完工时间优化效果优于遗传算法（GA）和灰狼优化（GWO）。
多目标优化改进：
- 自适应动态概率PSO：结合Pareto最优解集与高斯动态搜索，提升多样性；
- 混合模糊自适应PSO：融合模糊逻辑调整参数，处理模糊加工时间场景。
复杂约束处理：
- 运输时间考量：加入邻域搜索与竞争学习机制，解决物流协同问题；
- 能效优化：动态调整加工速度与机器开关策略，能耗降低10-15%。

五、求解框架设计与实验验证

典型框架流程：

编码与解码：将连续空间粒子映射为可行调度方案（如工序-机器矩阵）；
种群初始化：混合全局选择、局部选择与随机选择策略；
迭代优化：动态调整学习因子与变异概率，结合精英保留策略；
收敛判定：基于最大迭代次数或适应度变化率终止搜索。

实验数据集：

Brandimarte_DATA、Kacem：标准测试集，涵盖不同规模（如10×5、15×8）；
评价指标：最大完工时间（Cmax⁡Cmax）、机器总负荷（TloadTload）、多样性（SP）、收敛性（GD）。

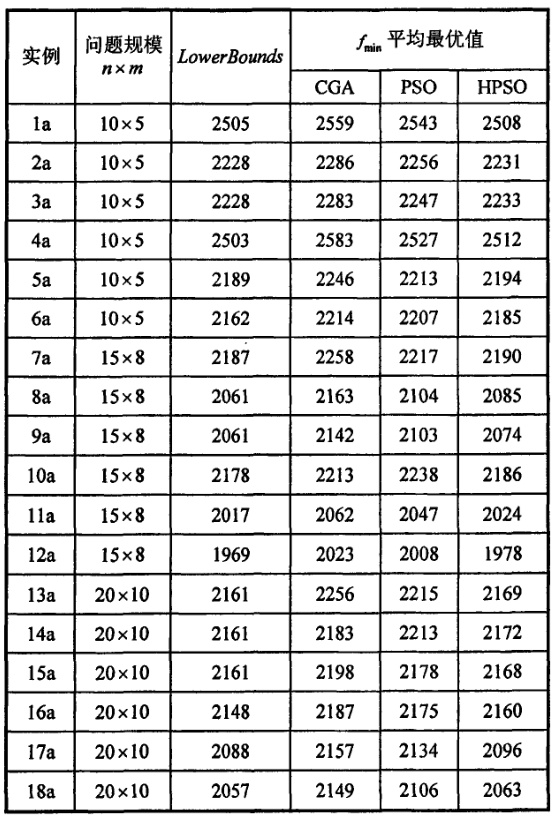
对比实验结果：

算法	最大完工时间优化率	收敛速度提升	适用场景
传统PSO	-	-	小规模单目标问题
改进离散PSO	8-12%	30-40%	中大规模FJSP
混合PSO-GA	10-15%	20-25%	多目标复杂约束场景
混沌多目标PSO	12-18%	50%	高维动态调度问题

六、研究展望

动态调度扩展：考虑机器故障、紧急插单等实时扰动；
跨领域融合：结合数字孪生、强化学习提升自适应能力；
绿色制造深化：集成碳排放、资源循环等多维度优化目标；
算法普适性：开发通用框架适配不同柔性车间场景。

结论：改进PSO算法通过离散化策略、混合优化机制与动态参数调整，显著提升了FJSP的求解效率与质量。未来需进一步探索算法在复杂工业环境中的工程化应用，推动智能制造系统优化。

📚2 运行结果

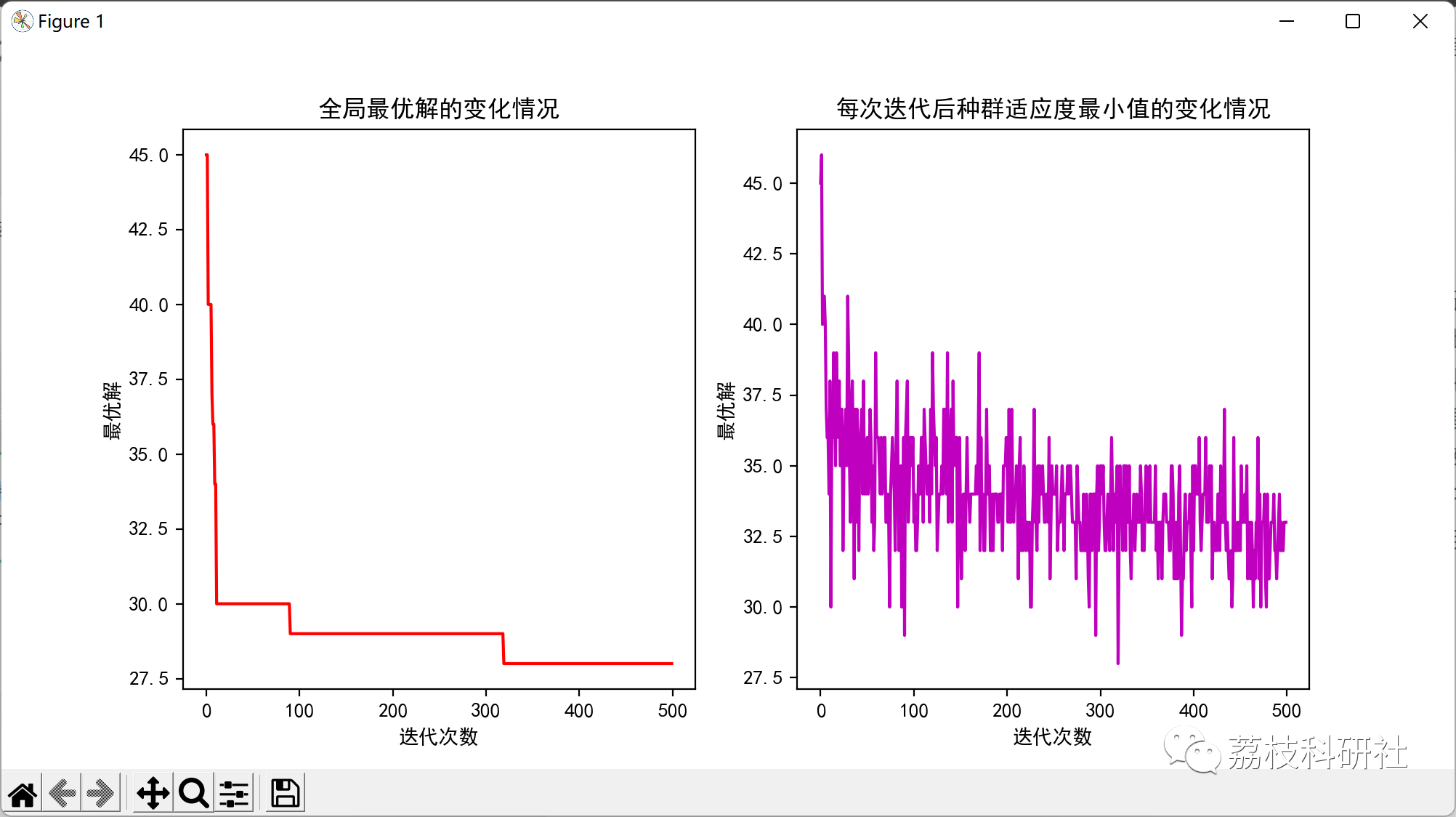
部分代码：

def calculate(x):
    # 输入:粒子位置，输出:粒子适应度值
    Tm = np.zeros(machine) #每个机器上的完工时间
    Te = np.zeros((workpiece, process)) #每个工序的完成时间
    array = handle(x) #经过处理后的工序部分

    for i in range(total_process):
        machine_index = int(x[total_process+(array[i][0]-1)*process+(array[i][1]-1)])-1 #contents数组中的纵坐标
        process_index = (array[i][0]-1)*process + (array[i][1]-1) #contents数组中的横坐标
        process_time = int(contents[process_index][machine_index])
        if array[i][1] == 1:
            Tm[machine_index] += process_time
            Te[array[i][0]-1][array[i][1]-1] = Tm[machine_index]
        else:
            Tm[machine_index] = max(Te[array[i][0]-1][array[i][1]-2], Tm[machine_index]) + process_time
            Te[array[i][0]-1][array[i][1]-1] = Tm[machine_index]
    return max(Tm)

def getinitbest(fitness,pop):
    # 群体最优的粒子位置及其适应度值
    gbestpop,gbestfitness = pop[fitness.argmin()].copy(),fitness.min()
    #个体最优的粒子位置及其适应度值,使用copy()使得对pop的改变不影响pbestpop，pbestfitness类似
    pbestpop,pbestfitness = pop.copy(),fitness.copy()
    return gbestpop,gbestfitness,pbestpop,pbestfitness