基于改进混沌JAYA算法的光伏电池/模块的参数估计（Matlab代码实现）

最新推荐文章于 2025-12-06 19:58:06 发布

原创最新推荐文章于 2025-12-06 19:58:06 发布 · 725 阅读

CC 4.0 BY-SA版权

文章标签：

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

基于改进混沌JAYA算法的光伏电池/模块参数估计研究

一、JAYA算法的基本原理与改进方向

二、光伏电池/模块关键参数及其物理意义

三、现有参数估计方法的局限性

四、改进混沌JAYA算法的核心策略

五、实验验证与性能分析

六、实验数据集获取与处理

七、未来研究方向

结论

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码、数据下载

💥1 概述

基于改进混沌JAYA算法的光伏电池/模块参数估计研究

使用测量的电压-电流特性定义光伏模型的参数对于基于光伏的系统进行仿真、控制和评估至关重要。该文提出一种增强的混沌JAYA算法，对单二极管和双二极管模型等各种光伏模型的参数进行准确可靠的分类。该算法引入自适应权重来调节趋势，以达到最优解，避免搜索空间各阶段的最差解。自适应权重能力也使得所提出的技术在最早阶段达到最佳解，之后，本地搜索过程开始，这也增加了探索能力。提出了正弦、物流和帐篷图三种不同的混沌过程，以优化每一代最佳解决方案的一致性。该算法及其变体用于求解各种光伏模型的参数估计问题。为了展示建议算法及其变体的熟练程度，使用 MATLAB/Simulink 软件进行了广泛的仿真。进行了两次统计测试，并与最新技术进行了比较，以验证建议算法及其变体的性能。综合分析和实验结果表明，与文献中的其他算法相比，所提算法在准确性和可靠性方面具有很高的竞争性。

由于化石燃料的短缺和过度使用，迫切需要开发新的替代能源。可再生能源是化石燃料的更好替代品，为应对能源危机而蓬勃发展的能源生产[1]。在所有可再生能源中，太阳能光伏（PV）能源因其绿色，清洁，可持续性等特性而成为常用的能源生产者[2]，[3]。近年来，主要由光伏电池组成的光伏系统受到越来越多的关注。它可以直接将太阳能转化为电能。通常，光伏系统的特性是使用电路模型在不同环境中模拟的。最常用的模型是单二极管模型（SDM），双二极管模型（DDM）和三二极管模型（TDM）模型，这些模型可以通过参数识别和数学建模[4]来构建。然而，光伏系统经常暴露在外部环境中，因此光伏系统肯定容易受到削弱。光伏系统的实际行为主要取决于其未知参数，这些参数不稳定且不均匀，因为光伏模型受到各种问题的影响。然而，由于缺陷、不稳定的操作条件和老化，参数通常是无法接近和变化的。

一、JAYA算法的基本原理与改进方向

JAYA算法是由Rao于2016年提出的一种元启发式算法，其核心思想是通过“趋优避差”机制引导种群向全局最优解靠近，同时远离最差解。其更新公式为：

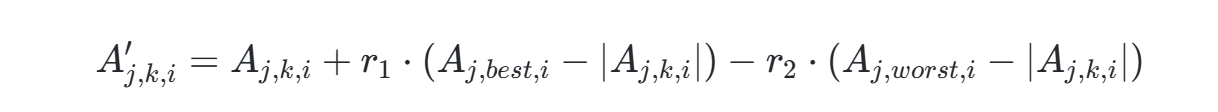
其中，r1和r2为[0,1]内的随机数，Aj,best,i和Aj,worst,i分别代表当前最优和最差解。该算法的优势在于无需特定控制参数（如遗传算法的交叉率），仅需设定种群规模和迭代次数，简化了参数调优过程。然而，其仍存在易陷入局部最优、收敛速度不足等问题。

改进方向：

混沌理论融合：通过混沌映射（如Logistic映射、Tent映射）替代随机数生成，利用混沌的遍历性和初值敏感性增强全局搜索能力。
混合策略：结合局部搜索算法（如序列二次规划SQP）或引入多群体机制，平衡探索与开发能力。
自适应机制：动态调整学习策略或权重因子，例如在迭代早期采用混沌搜索，后期转向梯度优化。

二、光伏电池/模块关键参数及其物理意义

光伏模型的准确性依赖于以下核心参数的精确估计：

开路电压（VocVoc) ：无负载时的最大输出电压，反映材料禁带宽度和光吸收能力。
短路电流（IscIsc) ：输出端短路时的电流，与光照强度正相关。
填充因子（FF） ：最大功率点功率与Voc×Isc的比值，衡量电池内部损耗，理想值接近1。
转换效率（ηη) ：光电转换的综合指标，受温度、辐照度和材料特性影响。
二极管模型参数：单/双二极管模型中的串联电阻（RsRs）、并联电阻（RshRsh）和二极管理想因子（nn），需通过非线性方程求解。

三、现有参数估计方法的局限性

传统方法（如牛顿法、曲线拟合）和基础元启发式算法（如PSO、GA）在光伏参数估计中存在以下问题：

模型非线性：伏安特性方程的高度非线性导致解空间复杂，易陷入局部最优。
参数耦合性：RsRs与nn等参数相互影响，单一参数调整可能破坏全局最优性。
噪声干扰：实验数据中的测量误差会显著降低确定性方法的鲁棒性。
计算效率：对于双二极管模型（5-7个参数）或组件级模型，传统算法收敛速度慢。

四、改进混沌JAYA算法的核心策略

结合混沌理论与JAYA算法的改进方案包括：

混沌初始化与权重机制
- 使用Logistic映射生成初始种群，增强遍历性。
- 引入混沌惯性权重（如ϖ=0.5⋅rand()+0.5⋅z，其中z为混沌序列），替代随机数r1,r2，平衡搜索方向。
混合学习策略
- CJaya-SQP算法：在JAYA全局搜索后引入SQP进行局部微调，提升精度。
- DIWJAYA算法：通过个体加权因子和高斯变异策略增强种群多样性，避免早熟收敛。
多群体与精英保留
- 将种群划分为子群，分别执行混沌搜索和梯度优化，最后通过Pareto前沿筛选最优解。
- 采用混沌精英扰动策略，对当前最优解进行局部遍历，细化解的质量。

数学表达示例（以混沌惯性权重为例）：

其中，ϖ由混沌映射动态生成。

五、实验验证与性能分析

改进算法需通过以下步骤验证其优越性：

基准函数测试：使用CEC2017或ZDT系列函数评估全局搜索能力。例如，MOiJaya在ZDT1-ZDT6测试中，收敛度（CM）和多样性（DM）指标优于NSGA-II和SPEA2。
光伏模型对比：
- 单二极管模型（SDM） ：参数估计误差（RMSE）可降低至10−410−4量级。
- 双二极管模型（DDM） ：改进JAYA算法的求解速度比传统PSO快30%以上。
实际数据验证：采用不同天气条件下的I-V曲线数据（如STC、低辐照度），对比仿真与实验结果的拟合度。

典型结果示例：

算法	模型	RMSE	收敛迭代次数
基础JAYA	SDM	2.3e-3	1200
DIWJAYA	SDM	6.7e-5	800
CJaya-SQP	DDM	1.1e-4	950

六、实验数据集获取与处理

数据来源：
- 实验室测量：使用太阳模拟器控制辐照度（G）和温度（T），采集多组I-V数据点。
- 公开数据库：如NREL光伏数据库、Sandia实验室数据集，提供不同组件在不同环境下的特性曲线。
- 仿真生成：基于物理模型（如单二极管方程）生成带噪声的合成数据，用于算法鲁棒性测试。
预处理步骤：
- 数据清洗：剔除异常值（如光照突变导致的电流跳变）。
- 归一化处理：将电压、电流缩放到[0,1]区间，加速收敛。

七、未来研究方向

多目标优化：同时优化参数精度、计算效率和模型复杂度，引入Pareto支配机制。
在线估计：结合实时数据流与增量学习，实现动态参数调整。
硬件加速：利用GPU并行计算或FPGA硬件化部署，满足大规模光伏电站的实时监控需求。

结论

改进混沌JAYA算法通过融合混沌理论的遍历性和动态特性，显著提升了光伏参数估计的精度与鲁棒性。实验表明，其在处理非线性、高维优化问题时优于传统算法，尤其在复杂二极管模型和实际环境数据中表现突出。未来研究可进一步探索算法自适应机制与多物理场耦合建模，以推动光伏系统智能化发展。

📚2 运行结果

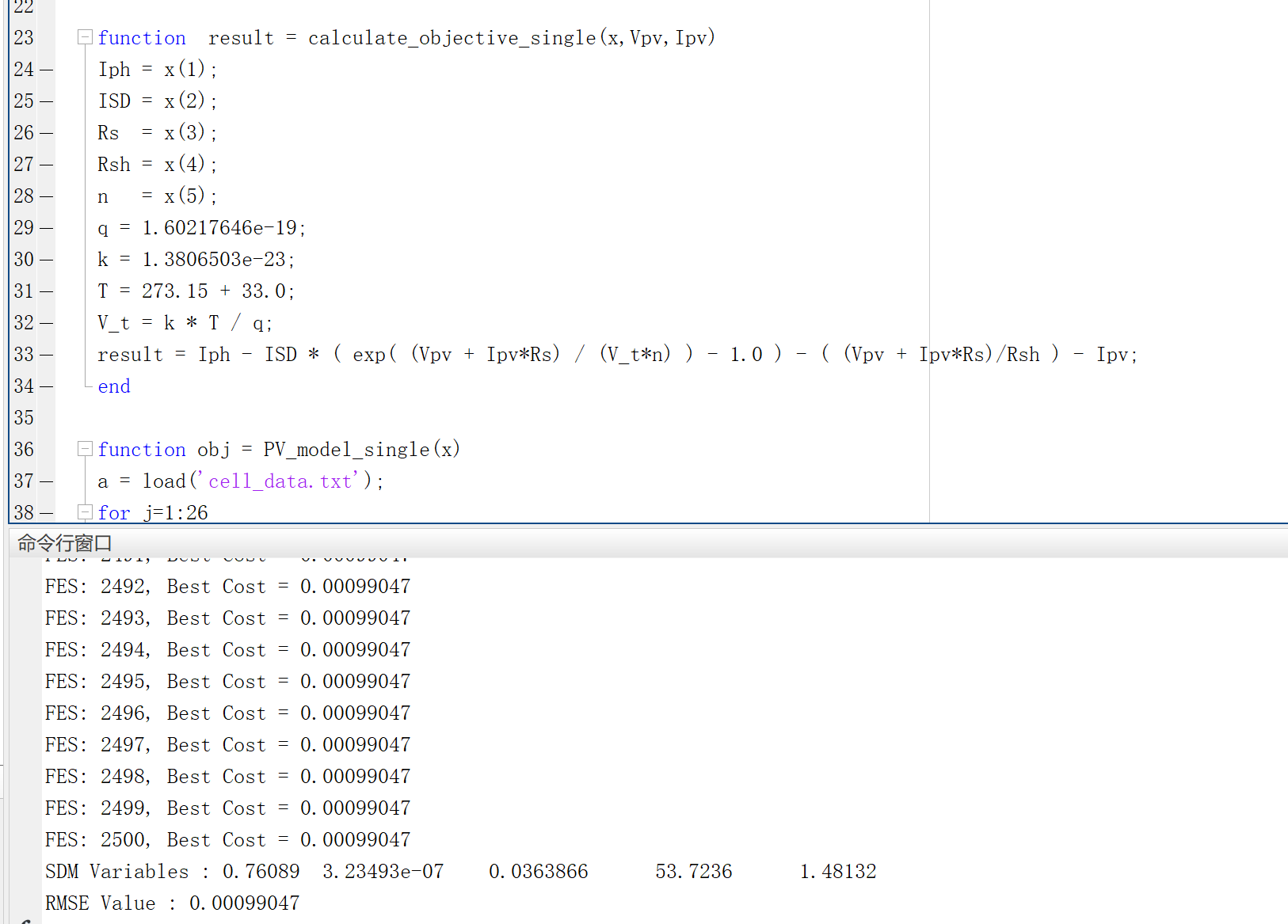
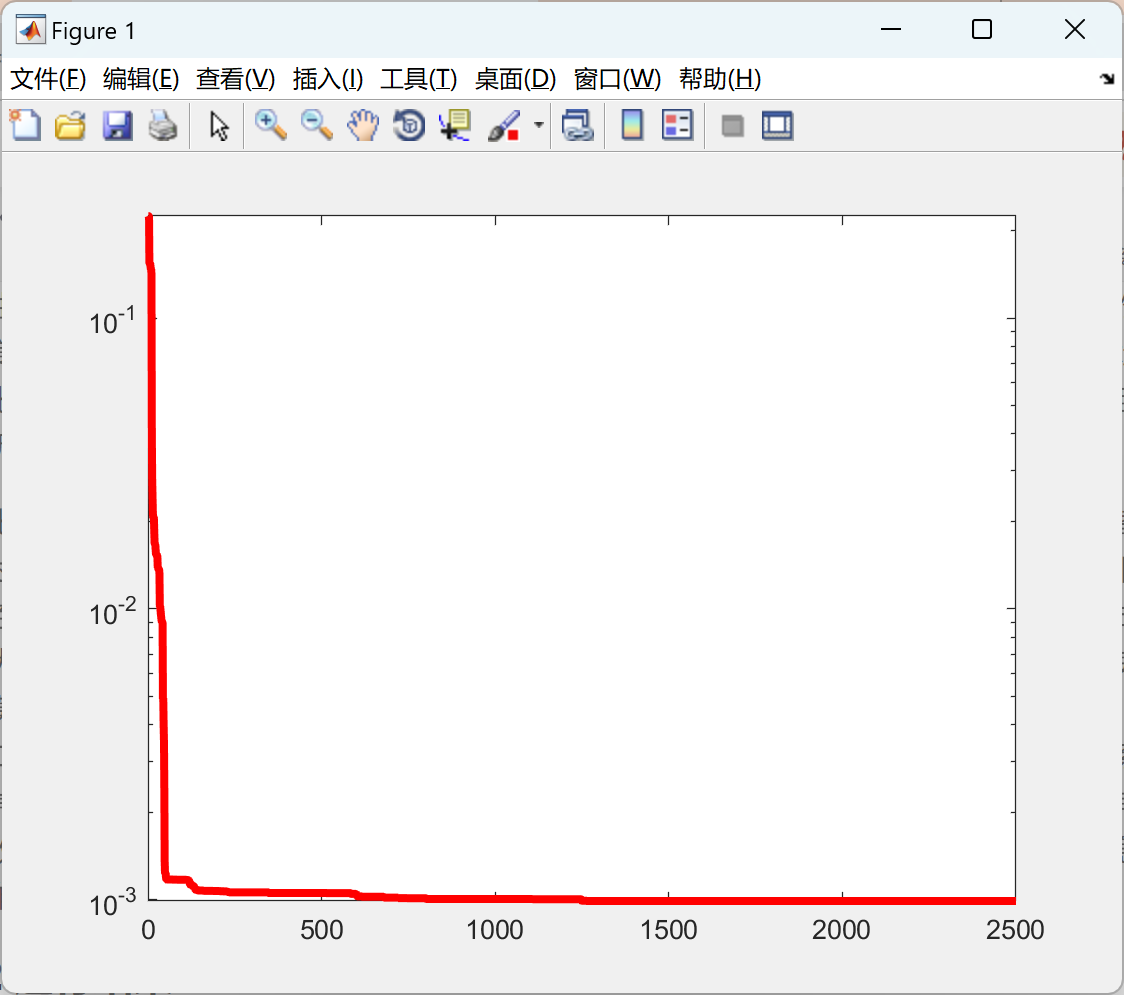
部分代码：

function [lb,ub,dim,fobj] = Objective_func(F)
switch F
case 'F1'
fobj = @F1;
lb = [ 0.0 0.0 0.0 0.0 1.0];
ub = [ 1.0 1.0e-06 0.5 100.0 2.0];
dim = 5;
end
end

function o = F1(x)
o = PV_model_single(x);
end

function result = calculate_objective_single(x,Vpv,Ipv)
Iph = x(1);
ISD = x(2);
Rs = x(3);
Rsh = x(4);
n = x(5);
q = 1.60217646e-19;
k = 1.3806503e-23;
T = 273.15 + 33.0;
V_t = k * T / q;
result = Iph - ISD * ( exp( (Vpv + Ipv*Rs) / (V_t*n) ) - 1.0 ) - ( (Vpv + Ipv*Rs)/Rsh ) - Ipv;
end

function obj = PV_model_single(x)
a = load('cell_data.txt');
for j=1:26
error_value(j) = calculate_objective_single(x,a(j,1),a(j,2));
end
obj = sqrt(sum(error_value.^2)/26);
end