👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
摘要:提出了一种基于遗传算法(ga)和随机重启爬坡(RRHC)的新型混合算法GA-RRHC,用于求解具有高灵活性(每项操作都可以由大量机器完成)的柔性作业车间调度问题(FJSSP)。特别地,不同的遗传算法交叉和简单变异算子与细胞自动机(CA)启发的邻域一起使用来执行全局搜索。该方法通过基于RRHC的局部搜索进行改进,使计算实现变得容易。在GA-RRHC中应用ca型邻域和上述两种技术进行杂交,得到了新颖的点,易于理解和实现。GA-RRHC的测试采用了文献中广泛使用的四组实验,并将其结果与使用相对百分比偏差(RPD)和Friedman检验的六种最新算法进行比较。实验表明,对于FJSSP实例,GA-RRHC算法具有较高的灵活性,是一种较有竞争力的方法。
关键词:柔性作业车间调度实例;遗传算子;局部搜索方法;元胞自动机
一、研究背景与意义
在制造业向智能化、柔性化方向发展的背景下,高柔性作业车间调度问题(Flexible Job-Shop Scheduling Problem, FJSP)成为生产调度中的核心挑战。FJSP允许每个工件的工序在多台可选机器上加工,这增加了调度的灵活性,但也显著提高了问题的复杂性。传统优化方法(如精确算法、启发式算法)在解决大规模FJSP时,常面临计算复杂度高、解质量差或易陷入局部最优等问题。因此,研究高效、鲁棒的优化算法对于提升生产效率、降低生产成本具有重要意义。
二、问题描述
高柔性作业车间调度问题(FJSP)的目标是在满足各种约束条件下,合理安排工件在机器上的加工顺序和时间,以优化某种性能指标,如最小化完工时间、最大化机器利用率等。具体而言,FJSP涉及多个工件、多种机器、不同的工艺路线以及各种约束条件,其复杂性随着问题规模的扩大而显著增加。
三、算法设计
1. 遗传算法(GA)
遗传算法是一种模拟生物进化过程的优化算法,通过选择、交叉、变异等操作不断迭代产生更优的解。在FJSP中,GA能够有效地探索解空间,避免陷入局部最优解。然而,传统的GA容易陷入局部最优解,导致搜索停滞。
2. 随机重启爬坡(RRHC)
RRHC是一种简单而有效的局部搜索算法,能够快速地在解的邻域内搜索更优解。当算法陷入局部最优时,RRHC通过随机生成新的初始解,并进行多次爬山搜索,以跳出局部最优,寻找更好的解。
3. GA-RRHC混合优化算法
将GA的全局搜索能力和RRHC的局部搜索能力相结合,形成GA-RRHC混合优化算法。该算法的主要步骤如下:
-
初始化阶段:随机生成初始种群,每个个体代表一个FJSP的可行调度方案。个体编码采用两层编码方式,第一层表示工序的加工顺序,第二层表示每个工序所选择的机器。
-
遗传算法操作:
- 选择操作:采用轮盘赌选择、锦标赛选择等策略,根据个体的适应度值选择优秀的个体进入下一代。
- 交叉操作:采用单点交叉、多点交叉、均匀交叉等方法,将两个父代个体的部分信息进行交换,产生新的子代个体。针对FJSP的特点,设计定制的交叉操作,如基于工序顺序的交叉和基于机器分配的交叉。
- 变异操作:采用反转变异、插入变异、交换变异等方法,对个体中的部分基因进行改变,增加种群的多样性。根据FJSP的特性设计合适的变异操作,如随机选择机器分配进行变异。
-
元胞自动机邻域局部搜索:引入元胞自动机(CA)的概念,将种群中的每个个体看作一个元胞,并定义元胞的邻域结构。每个元胞根据其邻域内的其他元胞的信息进行局部搜索,提高算法的局部探索能力。
-
随机重启爬山:当算法陷入局部最优时,触发RRHC策略。设定重启条件,如当算法在一定迭代次数内没有找到更好的解时,随机生成新的初始解,并进行多次爬山搜索。
-
终止条件:设定算法的终止条件,如达到最大迭代次数或找到满足要求的解。
四、实验验证与结果分析
1. 实验设置
选取标准的FJSP测试算例进行实验,如Brandimarte数据集、Kacem数据集等。与其他先进的优化算法进行比较,如传统遗传算法、粒子群算法、蚁群算法等。
2. 评价指标
- 求解质量:比较不同算法所获得的最佳解、平均解和最差解,以及解的稳定性。
- 收敛速度:比较不同算法的收敛速度,以及达到最优解所需的迭代次数。
- 鲁棒性:比较不同算法在不同参数设置下的性能表现,以及对不同规模问题的适应性。
3. 实验结果
实验结果表明,GA-RRHC算法在求解质量、收敛速度和鲁棒性方面均优于传统算法。具体而言:
- 求解质量:GA-RRHC算法能够找到更优的解,且解的稳定性更高。
- 收敛速度:GA-RRHC算法能够更快地收敛到最优解,减少了迭代次数。
- 鲁棒性:GA-RRHC算法在不同参数设置下和不同规模问题上均表现出良好的适应性。
五、算法优势与不足
1. 优势
- 全局搜索能力强:GA的全局搜索能力使得算法能够有效地探索解空间,避免陷入局部最优解。
- 局部搜索效率高:RRHC的局部搜索能力使得算法能够在解的邻域内快速找到更优解。
- 适应性强:GA-RRHC算法对不同规模和不同约束条件的FJSP均表现出良好的适应性。
2. 不足
- 参数调整复杂:算法中涉及多个参数,如种群规模、交叉概率、变异概率等,参数调整复杂且对算法性能影响较大。
- 计算复杂度高:随着问题规模的扩大,算法的计算复杂度显著增加,可能导致求解时间过长。
六、未来研究方向
1. 参数自适应调整
进一步研究GA-RRHC算法的参数自适应调整策略,如动态调整交叉概率、变异概率、邻域大小等参数,以提高算法的鲁棒性和适应性。
2. 与其他优化算法融合
将GA-RRHC算法与其他先进的优化算法进行融合,如与深度强化学习算法结合,利用深度学习的特征提取能力提高算法的求解效率。
3. 应用于实际生产场景
将GA-RRHC算法应用于实际生产场景,如智能制造、柔性生产线等,解决实际生产中的调度问题。通过实际应用验证算法的有效性和实用性。
📚2 运行结果
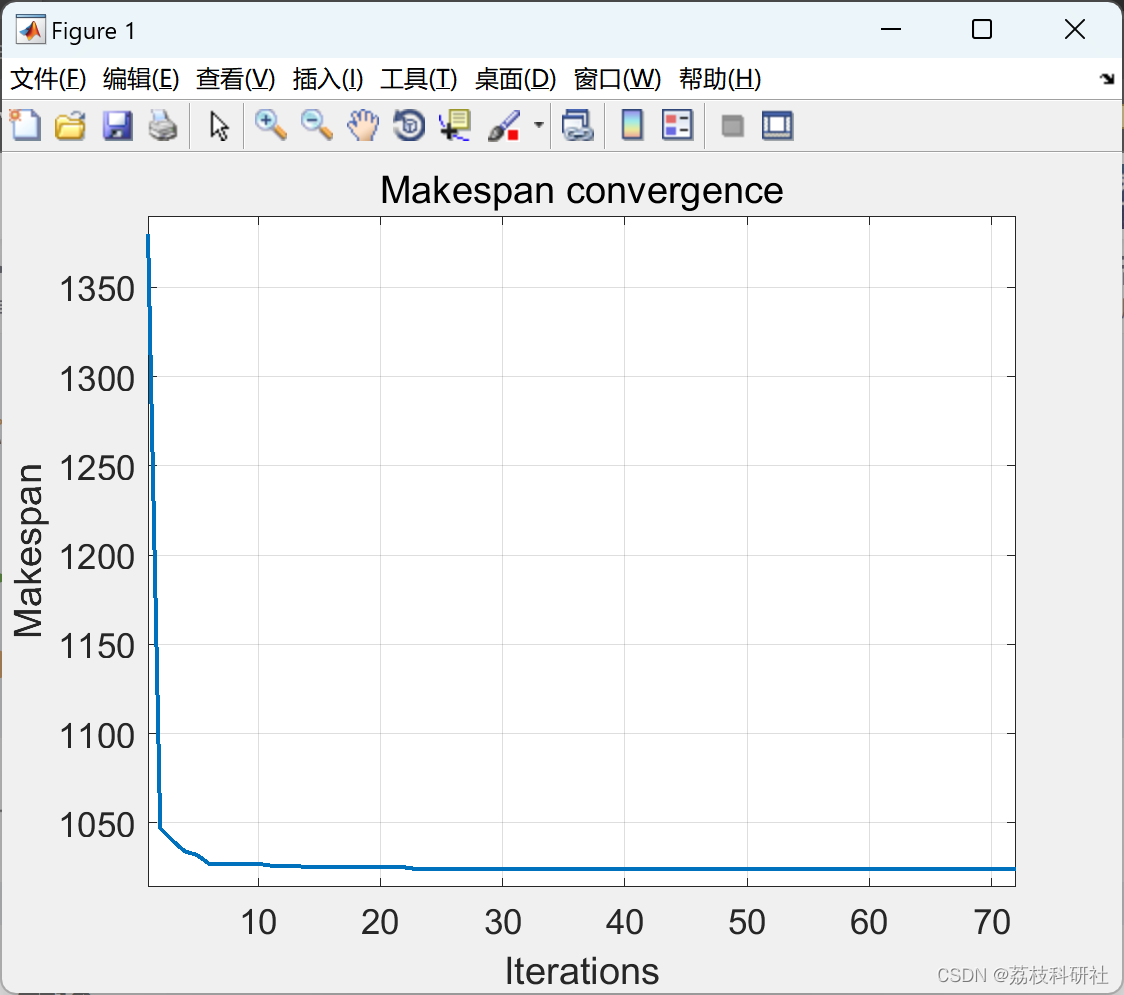


部分代码:
%Read data
function [numeroTrabajos, numeroMaquinas, numeroOperaciones, vectorNumOperaciones, vectorInicioOperaciones, vectorOperaciones, tablaTiempos, tablaMaquinasFactibles] = leerDatosProblema(nombreArchivo)
%The function reads the data table of the problem and returns the number of jobs, the number of machines,
%the vector with the number of operations per job, the vector with the previous operation number where each machine starts,
%the base vector with the number of operations per job, the base vector with the repeated operations for each job (1,...,1,2,...,2,...,n...,n...n),
%the table (operations/machines), the vector of the starting operation number of each job, the time table of each machine
%and the feasible machines for each operation
%Data format:
%in the first line there are (at least) 2 numbers: the first is the number of jobs and the second the number
%of machines (the 3rd is not necessary, it is the average number of machines per operation)
%Every row represents one job: the first number is the number of operations of that job, the second number
%(let's say k>=1) is the number of machines that can process the first operation; then according to k, there are
%k pairs of numbers (machine,processing time) that specify which are the machines and the processing times;
%then the data for the second operation and so on...
%Example: Fisher and Thompson 6x6 instance, alternate name (mt06)
%6 6 1
%6 1 3 1 1 1 3 1 2 6 1 4 7 1 6 3 1 5 6
%6 1 2 8 1 3 5 1 5 10 1 6 10 1 1 10 1 4 4
%6 1 3 5 1 4 4 1 6 8 1 1 9 1 2 1 1 5 7
%6 1 2 5 1 1 5 1 3 5 1 4 3 1 5 8 1 6 9
%6 1 3 9 1 2 3 1 5 5 1 6 4 1 1 3 1 4 1
%6 1 2 3 1 4 3 1 6 9 1 1 10 1 5 4 1 3 1
%first row = 6 jobs and 6 machines 1 machine per operation
%second row: job 1 has 6 operations, the first operation can be processed by 1 machine that is machine 3 with processing time 1.
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








