LeetCode——72. 编辑距离

最新推荐文章于 2025-06-10 17:50:05 发布

文艺范ya

最新推荐文章于 2025-06-10 17:50:05 发布

阅读量195

点赞数 1

CC 4.0 BY-SA版权

分类专栏： C++ 动态规划 JAVA 文章标签：字符串 leetcode 算法数据结构 java

本文链接：https://blog.youkuaiyun.com/FYPPPP/article/details/110285921

JAVA 同时被 3 个专栏收录

182 篇文章

订阅专栏

C++

85 篇文章

订阅专栏

动态规划

21 篇文章

订阅专栏

本文介绍了一种计算两个字符串之间的编辑距离的方法，通过动态规划解决这一问题。编辑距离是指通过插入、删除或替换字符将一个字符串转换为另一个字符串所需的最少操作次数。文章提供了详细的算法步骤，并附带了C++和Java实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述：

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数。

你可以对一个单词进行如下三种操作：
插入一个字符
删除一个字符
替换一个字符

示例 1：
输入：word1 = “horse”, word2 = “ros”
输出：3
解释：
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)

示例 2：
输入：word1 = “intention”, word2 = “execution”
输出：5
解释：
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)

题解：
1.动态规划

2.定义 dp[i][j]
2.1. dp[i][j] 代表 word1 中前 i 个字符，变换到 word2 中前 j 个字符，最短需要操作的次数
2.2. 需要考虑 word1 或 word2 一个字母都没有，即全增加/删除的情况，所以预留 dp[0][j] 和 dp[i][0]。

3.状态转移
3.1. 增，dp[i][j] = dp[i][j - 1] + 1
3.2. 删，dp[i][j] = dp[i - 1][j] + 1
3.3. 改，dp[i][j] = dp[i - 1][j - 1] + 1
3.4. 按顺序计算，当计算 dp[i][j] 时，dp[i - 1][j] ， dp[i][j - 1] ， dp[i - 1][j - 1] 均已经确定了
3.5. 配合增删改这三种操作，需要对应的 dp 把操作次数加一，取三种的最小
3.6. 如果刚好这两个字母相同 word1[i - 1] = word2[j - 1] ，那么可以直接参考 dp[i - 1][j - 1] ，操作不用+1。

dp数组：
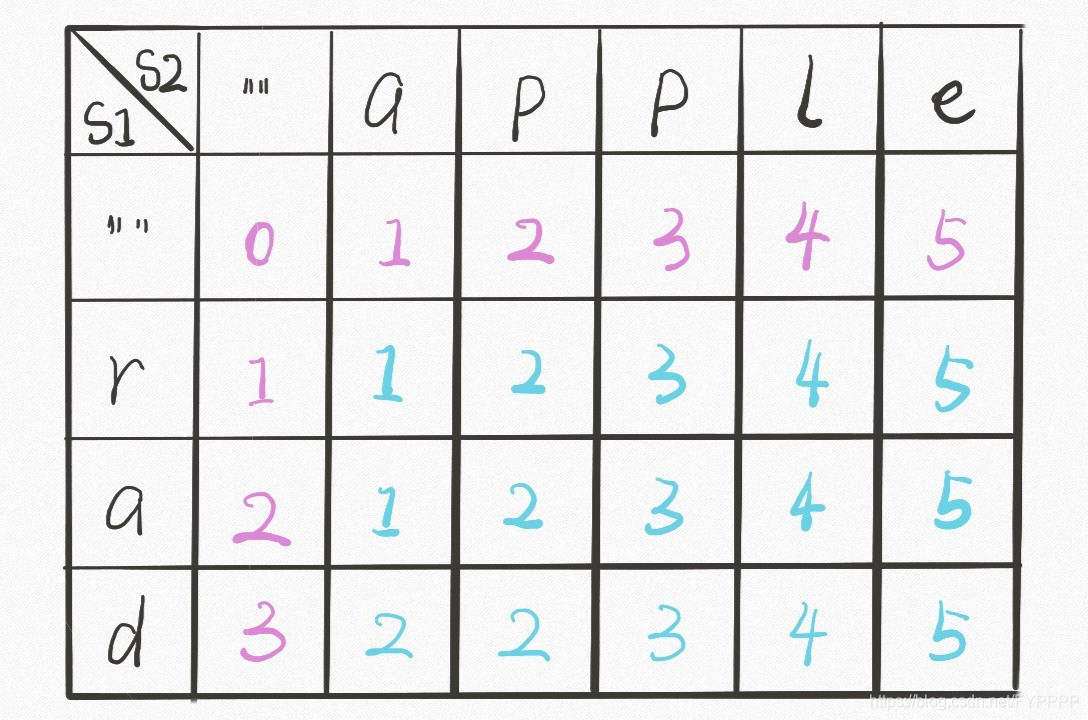
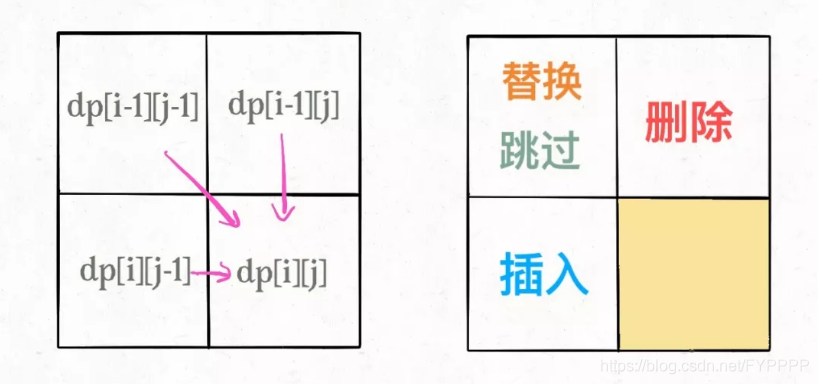
在这里插入图片描述

C++代码如下：

class Solution {
public:
    int minDistance(string word1, string word2) {
        int n=word1.size();
        int m=word2.size();
        vector<vector<int> >dp(n+1,vector<int>(m+1,0));
        for(int i=1;i<=n;i++){
            dp[i][0]=i;
        }
        for(int j=1;j<=m;j++){
            dp[0][j]=j;
        }
        for(int k=1;k<=n;k++){
            for(int r=1;r<=m;r++){
                if(word1[k-1]==word2[r-1]){
                    dp[k][r]=dp[k-1][r-1];
                }
                else{
                    dp[k][r]=min(min(dp[k-1][r]+1,dp[k][r-1]+1),dp[k-1][r-1]+1);
                }
            }
        }
        return dp[n][m];
    }
};

JAVA代码如下：

class Solution {
    public int minDistance(String word1, String word2) {
        int n = word1.length();
        int m = word2.length();
        char[] ch1 = word1.toCharArray();
        char[] ch2 = word2.toCharArray();
        int[][] dp = new int[n + 1][m + 1];
        for (int i = 1; i <= n; i++) {
            dp[i][0] = i;
        }
        for (int j = 1; j <= m; j++) {
            dp[0][j] = j;
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (ch1[i - 1] == ch2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j] + 1, dp[i][j - 1] + 1), dp[i - 1][j - 1] + 1);
                }
            }
        }
        return dp[n][m];
    }
}