堆排序详细解析

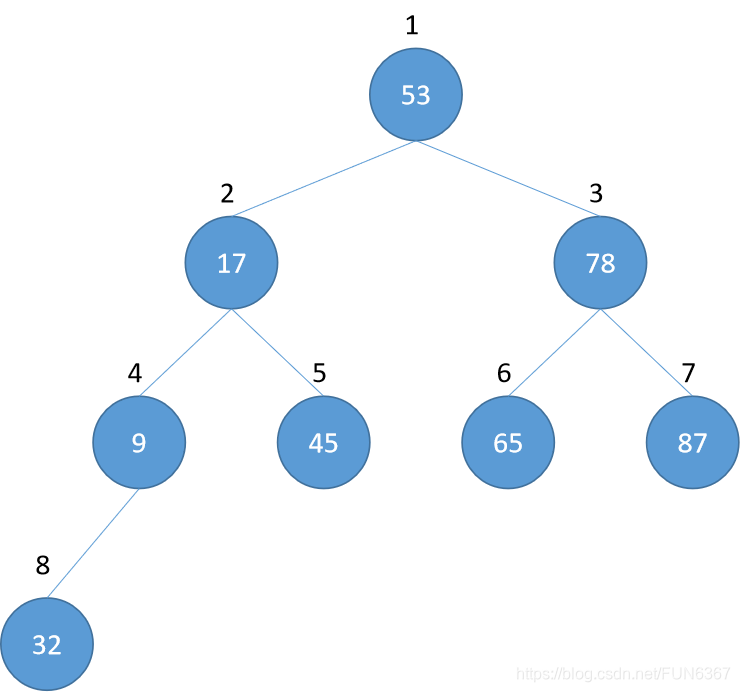
1、堆排序的数据结构-顶堆：一种完全二叉树（C++中的优先队列）

大顶堆：每个结点的值都比它的孩子结点（如果有）的值大
小顶堆：每个结点的值都比它的孩子结点（如果有）的值小

2、完全二叉树的性质：

对于有n个结点的完全二叉树：
结点编号为i的节点有左孩子等价于i*2 <= n且左孩子结点编号为i*2
结点编号为I的结点有右孩子等价于i*2 + 1 <= n且右孩子结点编号为i*2 + 1
编号为n**/2向下取整**的节点为，最后一个有孩子的节点

3、堆排序：升序用大顶堆；降序用小顶堆

4、建堆过程（从下向上）

从下向上建堆意味着，每次调整第k个结点时，它的孩子结点（如果有）都已经符合堆结构，此外所有的叶子结点都符合堆结构

void BuildMaxHeap(int A[], int len){   //从最后一个有孩子的节点向上调整，叶节点不需要调整
    for(int i = len/2; i >= 1; i --){
        AdjustDown(A, i, len);
    }
}

5、调整过程（算法核心）

void AdjustDown(int A[], int k, int len){

    if(k * 2 > len){    //如果结点k没有孩子则调整结束
        return;
    }

    int i = k * 2;      //工作指针指向k的左孩子

    if(A[i] < A[i + 1] && i < len){    //如果k有右孩子 且 右孩子的值比左孩子的值大，则i指向右孩子
        i ++;
    }

    if(A[k] >= A[i]){   //如果k的值大于等于值最大的孩子，则调整结束
        return;
        
    }else{              //如果k的值小于值最大的孩子，则交换A[i] 与 A[k]的值，然后继续调整结点i
        swap(A[i], A[k]);
        AdjustDown(A, i, len);
    }
}

6、建堆算法过程模拟：

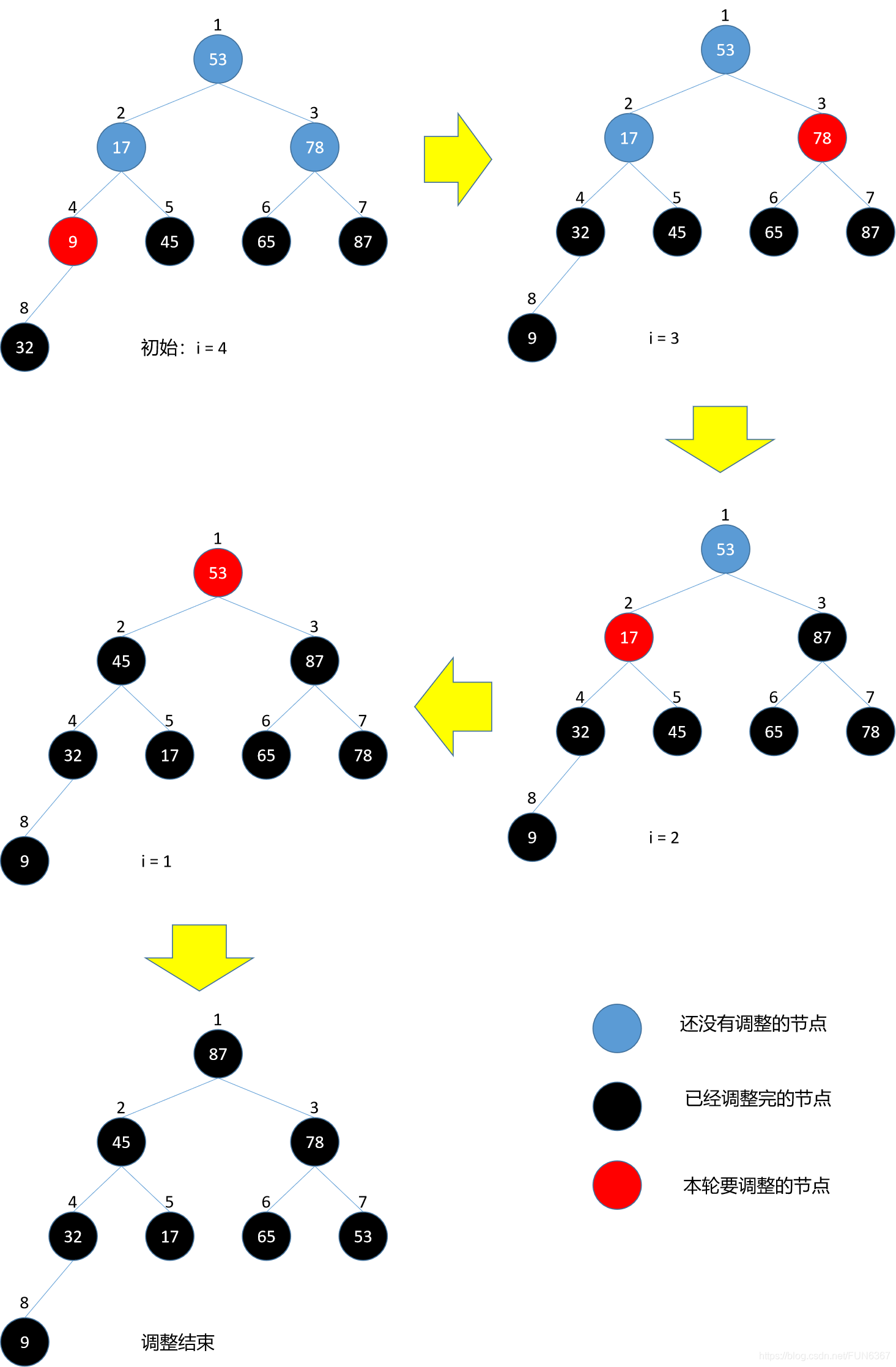
注意每一步调整中都包含很多步骤：
例如，最后一步中的i=1的调整中
1号结点的右孩子3号节点的值大于1号节点，所以交换1号节点和3号节点的值，但是交换完之后3号节点就不满足堆结构了，因此需要再调整3号节点，依次递归调整