笛卡尔树，treap树

---

一、前言

笛卡尔树：笛卡尔树是一种二叉树，每一个节点由一个键值二元组 (𝑘,𝑤)
(k,w) 构成。要求 k 满足二叉搜索树的性质，而 w 满足小根堆的性质。
可以用数组下标作为k。
二叉树一层一层变大，每插入一个节点y就跟当前节点x比较，y > x，就把y插入到x右侧，把当前节点更新成y。否则往前找到第一个小于它的值，并把大的数字插入到x左侧，更新当前节点。
相当于维护了一个递增子序列。

1. 子树内的下标是一段连续的区间
2. 子树内的节点都大于等于u

---

二、算法

1.笛卡尔树

<1>（P1377 [TJOI2011] 树的序）

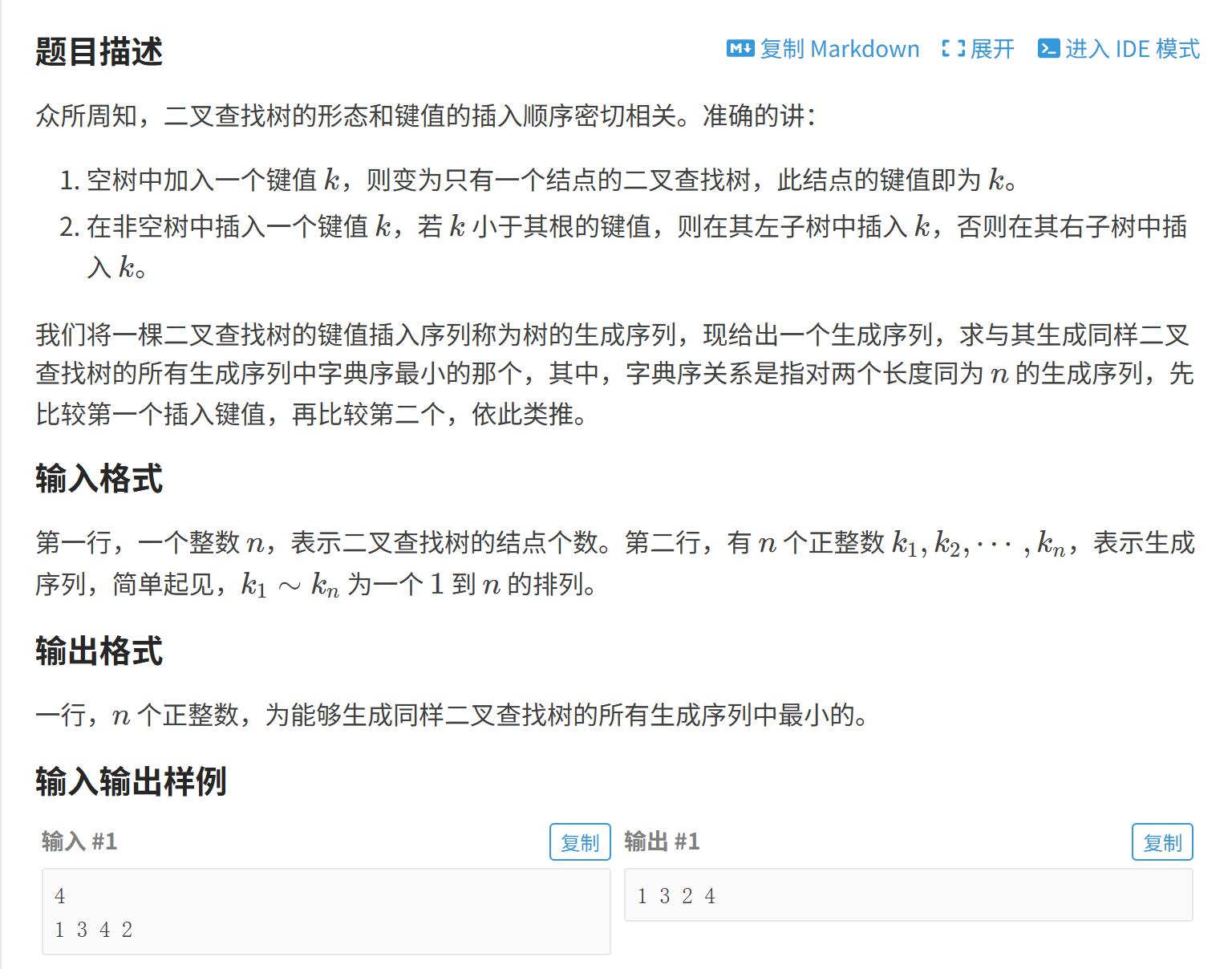
题解：
构建笛卡尔树 前序遍历
代码：

//   {\__/}
//   ( •̀‿•́)
//   /づ
#include<bits/stdc++.h>

using namespace std;
#define int long long

const int N = 1e5+10;
int n; int a[N];
vector<int>b[N];
int ls[N],rs[N];

void dfs(int re) {
   if(re == 0) return ;

   cout << re << ' ';
   dfs(ls[re]);
   dfs(rs[re]);
}

void solve() {
   cin >> n;

   int y = 0;

   for (int i = 1; i <= n; i++) {
       int x; cin >> x;
       if(y == 0) y = x;
       a[x] = i; //每个数字插入的位置
       ls[i] = 0; rs[i] = 0;
   }



//    // stk 维护笛卡尔树中节点对应到序列中的下标
//    for (int i = 1; i <= n; i++) {
//        int k = top;  // top 表示操作前的栈顶，k 表示当前栈顶
//        while (k > 0 && w[stk[k]] > w[i]) k--;  // 维护右链上的节点
//        if (k) rs[stk[k]] = i;  // 栈顶元素.右儿子 := 当前元素
//        if (k < top) ls[i] = stk[k + 1];  // 当前元素.左儿子 := 上一个被弹出的元素
//        stk[++k] = i;                     // 当前元素入栈
//        top = k;
//    }

   stack<int>s;

   for (int i = 1; i <= n; i++) {
       int st = 0;
       while(!s.empty() && a[s.top()] > a[i]) {
           st = s.top();
           s.pop();
       }
       if(!s.empty()) rs[s.top()] = i;
       //找到最下方的小于它的节点，自己作为它的右节点
       if(st) ls[i] = st;
       //找到最上面的大于它的节点，把大于它的节点作为左节点
       s.push(i);
       //存储当前右链
   }//构建笛卡尔树

   dfs(y);

}

signed main() {
   ios::sync_with_stdio(false);
   cin.tie(0); cout.tie(0);
   int _ = 1;
   // cin >> _;
   while(_--) solve();
}

---

三、总结