codeforces 1603B. Moderate Modular Mode

B. Moderate Modular Mode

YouKn0wWho has two even integers x and y. Help him to find an integer
n such that 1≤n≤2⋅1018 and nmodx=ymodn. Here, amodb denotes the
remainder of a after division by b. If there are multiple such
integers, output any. It can be shown that such an integer always
exists under the given constraints.

Input The first line contains a single integer t (1≤t≤105) — the
number of test cases.

The first and only line of each test case contains two integers x and
y (2≤x,y≤109, both are even).

Output For each test case, print a single integer n (1≤n≤2⋅1018) that
satisfies the condition mentioned in the statement. If there are
multiple such integers, output any. It can be shown that such an
integer always exists under the given constraints.

题意:给你两个数a和b,让你找到一个数x,使得 x%a=b%x

个人思路:当时看例子就觉得最后输出的答案应该是a*b+b,这样第一个式子是b,第二个也是b，然后代码一打出来第一个例子就寄了.然后觉得发现这种方式只能是a>b的情况下才能得出，然后得出当a小于b的时候,那个x应该是在a和b之间的

思路:
(1).a>b时,x=a+b(官方思路简单多了,哎蒻蓟)
(2).a=b时,x=a/x=b;
(3).a<b时,x=y-y%x/2
来说说第三个,我们要在a和b之间找到一个数使得式子成立 a>x&&x<b 也就是说求余之后数值都变了
根据这点,我们在想想a到b是不是有一段距离,b%a这是a和b之间两个数都没办法到达的地方,那么这个地方平分不就可以得到最后答案吗 (下图解释)

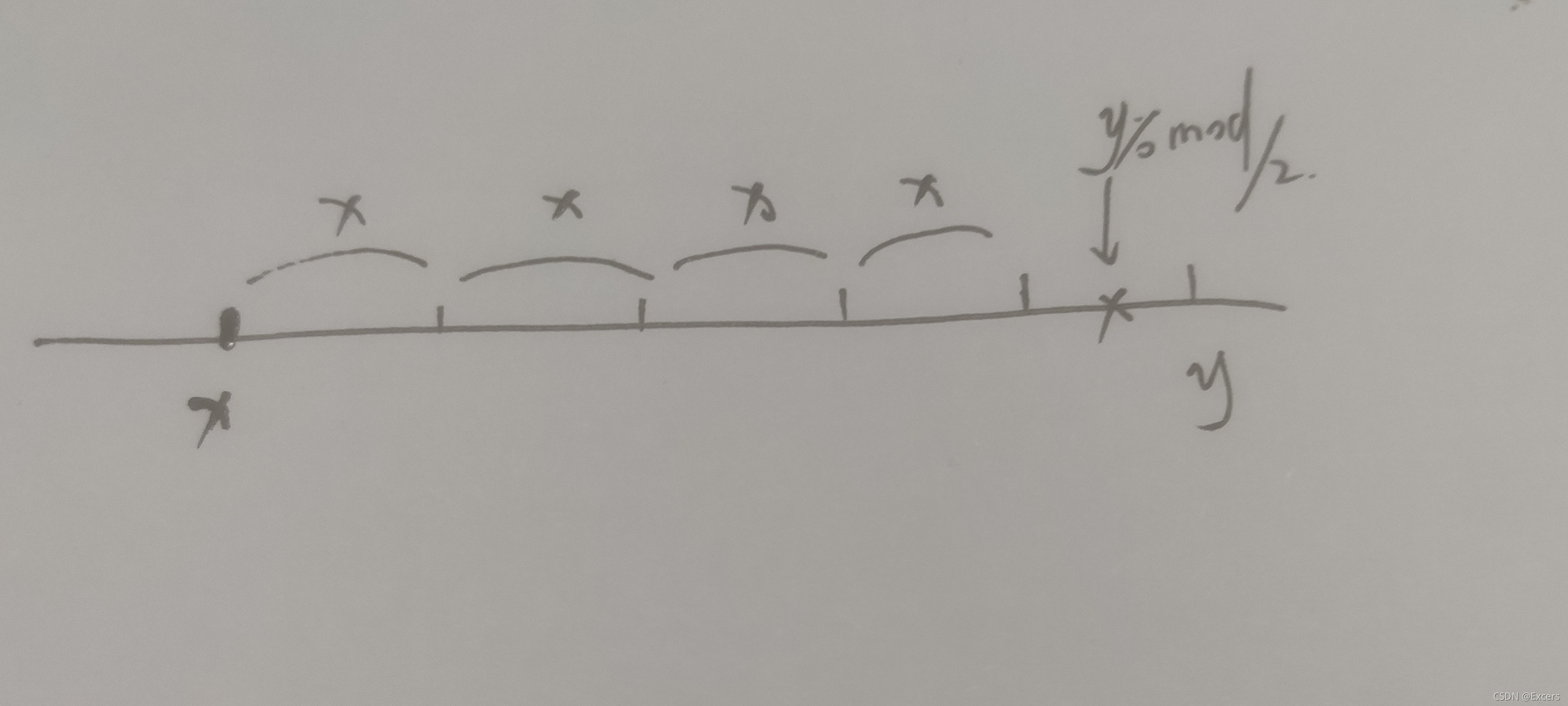
代码:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6+10,mod=998244353,INF=0x3f3f3f3f;
int a[N],b[N];
int main()
{
	int t;cin>>t;
	while(t--)
	{
		int x,y;cin>>x>>y;

		if(x<=y)cout<<y-(y%x)/2<<endl;
		else cout<<x+y<<endl;
	}
	return 0;
}