超牛牪犇Java之集合

集合(容器)

1.单列集合

2.双列集合

为什么有了数组还要有集合?

思考一下数组的弊端:

1.长度一旦确定不能更改

2.只能保存相同数据类型的元素

所以 可以联想到集合的好处:

1.长度可变

2.可以存放不同类型的元素

注意:集合中只能存储引用类型(对象类型)

collection类和子类的关系:

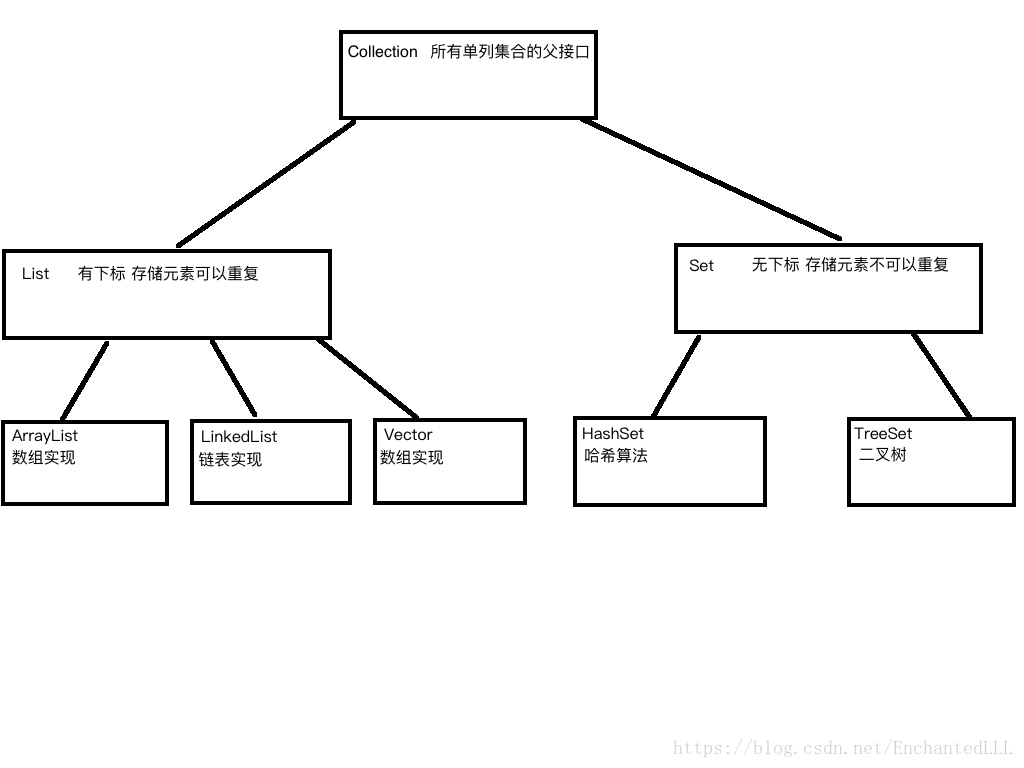
用多态的形式创建:

Collection collection = new ArrayList();

向集合中添加元素:(add方法返回的是布尔值)

直接向集合中存储基本类型的元素是 系统会进行自动装箱

返回值设计思想:能够使用下面的所有子接口(Set集合是有可能添加失败的)

boolean b1 = collection.add("a");
boolean b2 = collection.add(1);
boolean b3 = collection.add("c");

获取集合中元素个数:(没有返回值)

System.out.println(collection.size());

判断是否包含:(返回值为布尔类型)

boolean rel1 = collection.contains("a");

删除元素:(返回值为布尔类型)

boolean rel2 = collection.remove("c");

判断是不是空的集合:(返回值为布尔类型)

boolean rel3 = collection.isEmpty();

把集合转成数组:(Object类型的数组)

Object[] array = collection.toArray();
	for (Object object : array) {
	System.out.println(object);
}

清空数组:(不需要返回值)

collection.clear();

example:

需求:创建一个集合 保存5个学生 只打印学生的姓名(不打印年龄)

先建一个学生类:

class Student1{
	private String name;
	private int age;
	public Student1() {
		super();
	}
	public Student1(String name, int age) {
		super();
		this.name = name;
		this.age = age;
	}
	public String getName() {
		return name;
	}
	public void setName(String name) {
		this.name = name;
	}
	public int getAge() {
		return age;
	}
	public void setAge(int age) {
		this.age = age;
	}
	@Override
	public String toString() {
		return "Student [name=" + name + ", age=" + age + "]";
	}
}

建一个集合:

Collection collection = new ArrayList();
collection.add(new Student1("赵", 10));
collection.add(new Student1("钱", 11));
collection.add(new Student1("孙", 12));
collection.add(new Student1("李", 13));
collection.add(new Student1("周", 14));

把集合转成数组:(向上转型)

Object[] array = collection.toArray();

向下转型:(需要把数组的每一个对象都转化成student类型)

错误方法:(只把外壳改成了student类型 内部还是object类型的)

Student[] students = (Student[])array;

for (int i = 0; i < students.length; i++) {

        System.out.println(students[i].getName());

}

正确向下转型方法:

for (int i = 0; i < array.length; i++) {
		//将数组中的每一个对象转换
		Student1 student = (Student1)array[i];
		System.out.println(student.getName());
}