【算法】【动态规划】从1到n整数中1出现的次数：O(logn)算法

参考文献

有个专门的算法，参考文章：从1到n整数中1出现的次数：O(logn)算法_love music.的博客-优快云博客

算法描述

如题

算法原理

注意：

1.当now到达对应为值的时候只用管这个位有几个一就好了，不用管上一位有几个！

2.永远是left乘以right的位数，不是乘以left的位数

例如：当now为百位的时候，只需要关注从100~199有多少个1，不用管十位和个位的情况（如211算不算百位上的1呀），因为这些所有情况都在十位和个位包含了

过程模拟：

设now左边的几位的值为left，则left=4301

设now右边的几位的值为right，则right=0

now指向个位2的时候，因为left=4301，相当于在0000~4300这4301次经过了个位从0~9这个过程

又因为now=2>1,所以相当于在第4031（left=4030）次的时候个位经过了1

所以在个位出现过了(left+1)*1次1

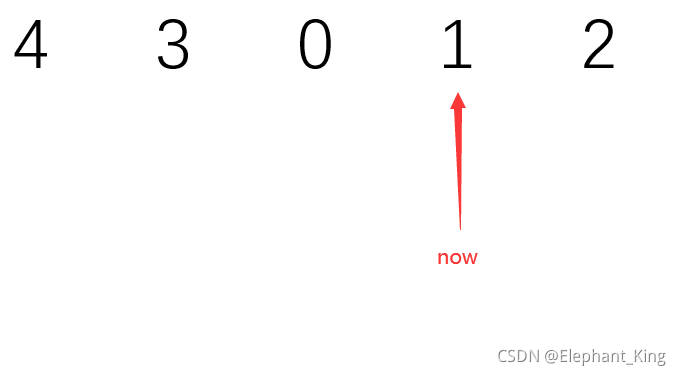
设now左边的几位的值为left，则left=430

设now右边的几位的值为right，则right=2

与上面同理，在十位经过了从000~429一共430次从0~9的变化，又因为是在十位，所以当十位等于1时，出现了10 11 12 13 14 15 16 17 18 19十次1，而且与个位等于1的情况不同。

又因为now=1=1，所以说明第431（left=430）次从0~9的过程1还没有完全走完10 11 12 13 14 15 16 17 18 19这十次，所以需要根据right来判断进行了几次

right=2，说明只有10 11 12三次

所以在十位上出现了left*10+right+1次1。

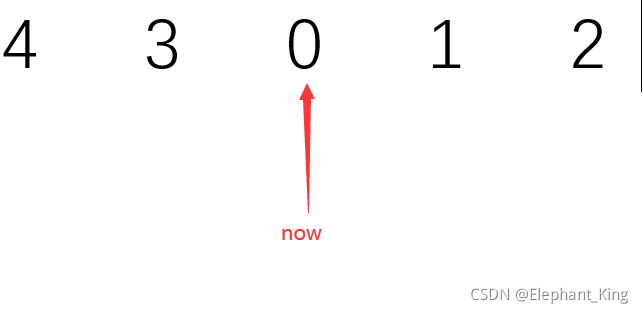
设now左边的几位的值为left，则left=43

设now右边的几位的值为right，则right=12

首先百位肯定经过了00~42共43次从0~9的过程，当百位等于1的时候，总共有100~199共100次等于1的数字

又因为now=0<1,说明第44次（left=43）的时候，压根1就没走到，所以一次也没有

所以在百位，1出现的次数为left*100.

依次类推即可求出所有位上的

核心代码实现

        for(int i=0;i<t.length();i++){
            if(t[i]=='0'){          //等于零时
                //sum+=left*right的位数
                sum+=getNum(0,i-1)*pow(10,(t.length()-i-1));
            }
            else if(t[i]=='1'){         //等于1的时候
                //sum+=left*right的位数+right的值+1
                sum+=getNum(i+1,t.length()-1)+1+getNum(0,i-1)*pow(10,(t.length()-i-1));
            }
            else{   //大于1的时候
                //sum+=(left+1)*right的位数
                sum+=pow(10,(t.length()-i-1))*(getNum(0,i-1)+1);
            }
        }