【Linux服务器开发】1.4 布隆过滤器-判断海量数据中某条数据是否存在

诸如一些常见的问题，
(1)网络爬虫程序，不去爬相同的url页面？
(2)垃圾邮件过滤算法如何设计？
(3)缓存崩溃后造成的缓存击穿？
(4)FBI如何判断一个嫌疑人的名字是否已经在嫌疑名单上？
(5)使用word文档时，判断某个单词是否拼写正确？
这些判重的问题，有一些数据量不是很大，一般的数据结构就可以帮助我们完成我们的需求，但是，如果有下面
这样一个明确了十亿百亿的数量级的需求呢？
一个像Yahoo,Hotmail和Gmai 那样的公众电子邮件（email）提供商，总是需要过滤来自发送垃圾邮件的人的
垃圾邮件.一个办法就是记录下那些发垃圾邮件的email地址.由于那些发送者不停地在注册新的地址,全世界少
说也有几十亿个发垃圾邮件的地址,将他们都存起来则需要大量的网络服务器.如果用哈希表，每存储一亿email 
地址,就需要1.6GB的内存（用哈希表实现的具体办法是将每一个email 地址对应成一个八字节的信息指纹(详
见：googlechinablog.com/2006/08/blog-post.html,链接已经失效了),然后将这些信息指纹存入哈希表，
由于哈希表的存储效率一般只有50%，因此一个email地址需要占用十六个字节.一亿个地址大约要1.6GB, 即十
六亿字节的内存）.因此存贮几十亿个邮件地址可能需要上百GB的内存.除非是超级计算机，一般服务器是无法存
储的(该段引用谷歌数学之美).

2.看看是否有可供选择的数据结构来帮助我们判断在海量数据中某条数据是否存在

2.1 红黑树

2.1.1 从时间来分析

我们知道红黑树的搜索时间复杂度是LOG(n,2)-表示以2为底的对数，则对于100w条数据来说，搜索一条数据的时间大概需要20次【LOG(1000000,2) 约等于19.93】.这效率好像对比哈希的话好像就差了些.

2.1.2 从空间来分析

...

2.2 哈希表

2.2.1 从时间来分析

如果用哈希表，需要考虑的时间是O(1)和hash的时间.

2.2.2 从空间来分析

如第一节中提到的，在垃圾邮箱问题中，一个亿的邮箱大概需要1.6G的内存，那么10亿条数据就需要大概16G的内存.

2.2.3 为什么不适用哈希表

哈希表的存储效率一般只有 50%(为了避免高碰撞，一般哈希存到一半时都翻倍或采取其他策略)，所以很费内存.

看本文3.5节中给出的示例分析.

3.主角-布隆过滤器

3.1 基本概念

    布隆过滤器（Bloom Filter）是由布隆（Burton Howard Bloom）在1970年提出的。它实际上是由一
个很长的二进制向量和一系列随机映射函数组成，布隆过滤器可以用于检索一个元素是否在一个集合中。它
的优点是空间效率和查询时间都远远超过一般的算法，缺点是有一定的误识别率（假正例False 
positives，即Bloom Filter报告某一元素存在于某集合中，但是实际上该元素并不在集合中）和删除困
难，但是没有识别错误的情形（即假反例False negatives，如果某个元素确实没有在该集合中，那么
Bloom Filter 是不会报告该元素存在于集合中的，所以不会漏报）。

    如果想判断一个元素是不是在一个集合里，一般想到的是将所有元素保存起来，然后通过比较确定。链
表，树等等数据结构都是这种思路. 但是随着集合中元素的增加，我们需要的存储空间越来越大，检索速度
也越来越慢.不过世界上还有一种叫作散列表(又叫哈希表，Hash table)的数据结构.它可以通过一个
Hash函数将一个元素映射成一个位阵列（Bit Array）中的一个点. 这样一来，我们只要看看这个点是不是 
1就知道可以集合中有没有它了.这就是布隆过滤器的基本思想.

Hash面临的问题就是冲突。假设 Hash 函数是良好的，如果我们的位阵列长度为m个点，那么如果我们想
将冲突率降低到例如 1%, 这个散列表就只能容纳 m/100 个元素。显然这就不叫空间有效了(Space-
efficient）.解决方法也简单，就是使用多个Hash,如果它们有一个说元素不在集合中,那肯定就不在.
如果它们都说在，虽然也有一定可能性它们在说谎，不过直觉上判断这种事情的概率是比较低的.

优点：
    相比于其它的数据结构，布隆过滤器在空间和时间方面都有巨大的优势.布隆过滤器存储空间和插入/查
询时间都是常数.另外, Hash函数相互之间没有关系，方便由硬件并行实现.布隆过滤器不需要存储元素本
身，在某些对保密要求非常严格的场合有优势.
    布隆过滤器可以表示全集，其它任何数据结构都不能；
    k和m相同，使用同一组Hash函数的两个布隆过滤器的交并差运算可以使用位操作进行。

缺点：
    布隆过滤器的缺点和优点一样明显,误算率（False Positive）是其中之一.随着存入的元素数量
增加，误算率随之增加。但是如果元素数量太少，则使用散列表足矣.

    另外，一般情况下不能从布隆过滤器中删除元素. 我们很容易想到把位列阵变成整数数组，每插入一个
元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全的删除元素并非如此简单。
首先我们必须保证删除的元素的确在布隆过滤器里面. 这一点单凭这个过滤器是无法保证的。另外计数器回
绕也会造成问题.


总结来说：
    布隆过滤器是一种数据结构,比较巧妙的概率型数据结构（probabilistic datastructure),特点是高
效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”.相比于传统的List、Set、Map等数
据结构,它更高效,占用空间更少,但是缺点是其返回的结果是概率性(存在误差)的,而不是确切的.

注意:不同的数据结构有不同的适用场景和优缺点,你需要仔细权衡自己的需求之后妥善适用它们,布隆过滤器
就是践行这句话的代表.

3.2 关键字与注意点

关键字:

假阳(false positives)

概率型数据结构（probabilistic datastructure)

多个哈希函数(multiple hashfunctions)

简单一致散列(simple uniform hashing)

完全哈希(perfect hashing)（也是个链接)

注意点：

BloomFilter会出现假阳情况，但不会出现假阴的情况，即会出现【某个值不存在但被判定为存在】的情况，但是不存在【某个值存在但被判定为不存在】的情况.

BloomFilter提供正确的否定，但是可能错误的肯定.

3.3 算法的设计描述

一个空的布隆过滤器是一个有m个bits的bit array,每一个bit位都初始化为0,并且定义有k个不同的
hash function，每个都以uniform random distribution将元素hash到m个不同位置中的一个.
在下面的介绍中n为元素数，m为布隆过滤器或哈希表的slot数，k为布隆过滤器重hash function数.

为了add一个元素，用k个hash function将它hash得到bloom filter中k个bit位，将这k个bit位置1。

为了query一个元素，即判断它是否在集合中，用k个hash function将它hash得到k个bit位.若这k个bits全为
1，则推断此元素可能存在在集合中；若其中任一位不为1，则此元素比不在集合中（因为如果在，则在add时已
经把对应的k个bits位置为1）。

不允许remove元素，因为那样的话会把相应的k个bits位置为0，而其中很有可能有其他元素对应的位.因此
remove会引入false negative，这是绝对不被允许的。【基础布隆不支持，但布隆过滤器相关扩展中支持】

当k很大时，设计k个独立的hash function是不现实并且困难的。对于一个输出范围很大的hash function(例
如MD5产生的128 bits数），如果不同bit位的相关性很小，则可把此输出分割为k份。或者可将k个不同的初始
值（例如0,1,2, … ,k-1）结合元素，feed给一个hash function从而产生k个不同的数.

当add的元素过多时，即n/m过大时（n是元素数，m是bloom filter的bits数），会导致false positive
过高，此时就需要重新组建filter，但这种情况相对少见.

3.4 算法的简单推演

3.4.1 初始状态

假设有3个哈希函数，8个bits的bit array.

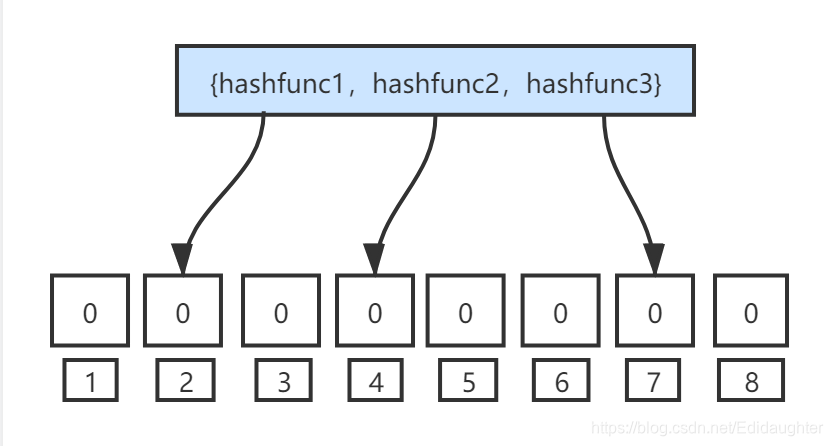
3.4.2 插入“baidu”这个字符串

经过hashfunc1，hashfunc2，hashfunc3这三个函数，将“baidu”这个字符串散列到了1,3,7这三个bit上.

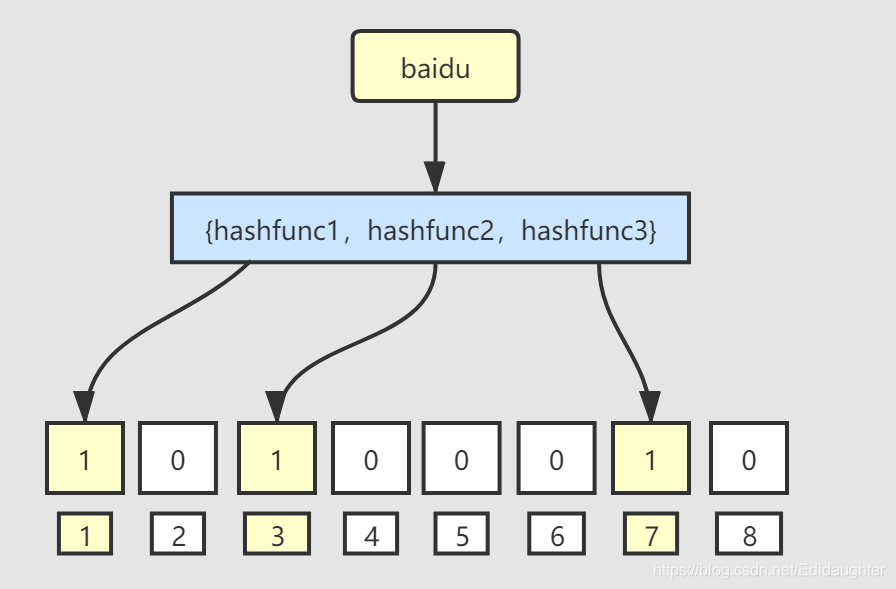
3.4.3 插入“tencent”这个字符串

经过hashfunc1，hashfunc2，hashfunc3这三个函数，将“baidu”这个字符串散列到了2,4,7这三个bit上.

3.4.4 查询“alibaba”的结果分析

(1)假阳: 如果查询“alibaba”的时候，如果根据hashfunc1，hashfunc2，hashfunc3这三个函数，返回了比如说1,3,4这三个bit位，那么程序还是会判断“alibaba”

这个字符串存在，但是实际上我们并没有存储过“alibaba”这个字符串，这就出现了“假阳”的情况.

(2)真阴:如果查询“alibaba”的时候，如果根据hashfunc1，hashfunc2，hashfunc3这三个函数，返回了比如说3,4,5这三个bit位，那么第五个bit上的值是0，一票否决，判定“alibaba”没有被存储过.

3.5 时间与空间上的优势

当可以承受一些误报时，布隆过滤器比其它表示集合的数据结构有着很大的空间优势。例如self-balance BST, tries, hash table或者array, chain，它们中大多数至少都要存储元素本身，对于小整数需要少量的bits，对于字符串则需要任意多的bits（tries是个例外，因为对于有相同prefixes的元素可以共享存储空间）；而chain结构还需要为存储指针付出额外的代价。对于一个有1%误报率和一个最优k值的布隆过滤器来说，无论元素的类型及大小，每个元素只需要9.6 bits来存储. 这个优点一部分继承自array的紧凑性，一部分来源于它的概率性。如果你认为1%的误报率太高，那么对每个元素每增加4.8bits，我们就可将误报率降低为原来的1/10。add和query的时间复杂度都为O(k)，与集合中元素的多少无关，这是其他数据结构都不能完成的。

如果可能元素范围不是很大，并且大多数都在集合中，则使用确定性的bit array远远胜过使用布隆过滤器。因为bit array对于每个可能的元素空间上只需要1 bit，add和query的时间复杂度只有O(1)。注意到这样一个哈希表（bit array）只有在忽略碰撞并且只存储元素是否在其中的二进制信息时，才会获得空间和时间上的优势，而在此情况下，它就有效地称为了k=1的布隆过滤器.

而当考虑到碰撞的时候，对于有m个槽的bit array或者其他哈希表（即k=1的布隆过滤器），如果想要保证1%的误判率，则这个bit array只能存储m/100个元素，因而有大量的空间被浪费，同时也会使得空间复杂度急剧上升，这显然不是节省空间的.解决的方法很简单，使用k>1的布隆过滤器，即k个hash function将每个元素改为对应于k个bits，因为误判度会降低很多，并且如果参数k和m选取得好，一半的m可被置为为1，这充分说明了布隆过滤器是在空间使用上是有效的.

文中【三. 举例说明】给出空间优势的实例

3.6 哈希函数的选择

常见的应用比较广的hash函数有MD5， SHA1， SHA256，一般用于信息安全方面，
比如签名认证和加密等.比如我们传输文件时习惯用对原文件内容计算它的MD5值，
生成128 bit的整数，通常我们说的32位MD5值，是转换为HEX格式后的32个字符.

另外还有MurmurHash算法,
◼MurmurHash是2008年发明的，相比较MD5， MurMurhash不太安全（当然MD5也被
破译了,sha也可以被破译),但是性能是MD5的几十倍;MurmurHash有很多个版
本， MurmurHash3修复了MurmurHash2的一些缺陷同时速度还要快一些，因此很多
开源项目有用，比如nginx,redis,memcashed,Hadoop等,比如用于计算一致性
hash等。
◼MurmurHash被比较好的测试过了，测试方法见
https://github.com/aappleby/smhasher, MurMurhash的实现也可以参考smhasher,或
者参考https://sites.google.com/site/murmurhash。
我们演示的布隆过滤器中的hash函数选择MurmurHash2算法.

3.7 代码路径

https://gitee.com/muten/bloomfilter/

代码中使用的哈希算法是MurmurHash2算法.

我的hpelitebook-Muten-1上的代码路径:/home/muten/LinuxServer/1.4/bloomfilter/bf

3.8 在线验证公式

测试网址：https://hur.st/bloomfilter/

3.9 设计和使用BloomFilter与一些说明

引自【https://www.cnblogs.com/allensun/archive/2011/02/16/1956532.html】

3.9.1 入参与使用步骤

应用时首先要先由用户决定要增加的最多元素个数n和希望的误差率P.这也是一个设
计完整的布隆过滤器需要用户输入的仅有的两个参数(加入hash种子则为3个),之后
的所有参数将由系统计算，并由此建立布隆过滤器.


n-用户决定要增加的最多元素个数(用户绝对,入参)
p-希望的误差率(用户绝对,入参)
m-内存大小，单位是bit(由n,p计算出)
k-哈希函数的个数，计算得出.

第一步.计算需要的内存大小m个bits

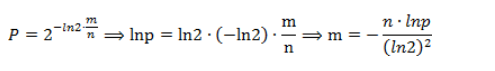
第二步.由m，n得到哈希函数的个数，至此系统所需的参数已经备齐，接下来加入n个元素至布隆过滤器中，再进行查询.

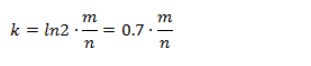
3.9.2 想保持错误率低，布隆过滤器的空间使用率需为50%

3.10 BloomFilter用例

Google著名的分布式数据库Bigtable使用了布隆过滤器来查找不存在的行或列，以减少磁盘查找的IO除数.
Squid 网页代理缓存服务器在 cache digests 中使用了也布隆过滤器.
Venti 文档存储系统也采用布隆过滤器来检测先前存储的数据.
SPIN 模型检测器也使用布隆过滤器在大规模验证问题时跟踪可达状态空间.
Google Chrome浏览器使用了布隆过滤器加速安全浏览服务.
在很多Key-Value系统中也使用了布隆过滤器来加快查询过程，如 Hbase，Accumulo，Leveldb，一般而言，
Value 保存在磁盘中，访问磁盘需要花费大量时间，然而使用布隆过滤器可以快速判断某个Key对应的Value是
否存在，因此可以避免很多不必要的磁盘IO操作，只是引入布隆过滤器会带来一定的内存消耗.