一篇全面的「因果强化学习」综述！！

最近刷到字节跳动「筋斗云人才计划」的前沿课题清单，一眼被 「基于 RL 的在线因果推断及决策」 抓住注意力！

细想一下：强化学习（RL）正在机器人控制、推荐系统等领域冲锋，但 「实时动态环境」+「复杂因果关系」 像两座大山 —— 传统 RL 依赖大量试错，还容易被 “虚假关联” 骗到，遇到环境变化就失灵。而 因果推断 × 在线 RL 的组合，相当于给智能体装上 “实时因果雷达”：既能拆解复杂场景里的因果逻辑，又能动态适应环境变化，解决样本低效、泛化能力弱的核心痛点。

巧的是，学术圈刚好有一篇权威综述 《A Survey on Causal Reinforcement Learning》，把 因果强化学习（CRL） 的理论、方法和应用全梳理透了，甚至暗合大厂对 “在线决策” 的技术诉求！从字节跳动的前沿布局，到学术领域的系统总结，CRL 正在成为连接「理论突破」和「工业落地」的关键枢纽。

接下来，我们就跟着这篇综述深挖：CRL 如何重塑 RL 的决策逻辑？在线场景里的因果推断有哪些核心挑战？甚至，或许能从技术拆解里，get 到大厂关注的 “人才能力密码”……

因果强化学习综述

文献地址： https://doi.org/10.48550/arXiv.2302.05209

摘要：虽然强化学习（RL）在许多领域的序贯决策问题中取得了巨大成功，但它仍然面临数据效率低下和缺乏可解释性的关键挑战。有趣的是，最近许多研究人员借鉴了因果关系领域的见解，催生了大量将因果关系的优点相结合的研究工作，很好地解决了强化学习面临的挑战。因此，整理这些因果强化学习（CRL）的研究工作，对CRL方法进行综述，并探讨因果关系对强化学习的潜在作用，具有重要的必要性和意义。特别地，我们根据现有的CRL方法是否预先给定基于因果关系的信息，将其分为两类。我们进一步从不同模型的形式化角度分析了每一类，包括马尔可夫决策过程（MDP）、部分可观测马尔可夫决策过程（POMDP）、多臂老虎机（MAB）和动态治疗方案（DTR）。此外，我们总结了评估指标和开源资源，同时讨论了新兴应用以及CRL未来发展的前景。

关键词：因果强化学习；因果发现；因果推断；马尔可夫决策过程；序贯决策

一、引言

强化学习（RL）旨在让智能体学习一个策略（从状态到动作的映射函数），以最大化其在环境中获得的期望奖励。它通过试错机制来解决序贯决策问题，即智能体与环境进行交互。由于其在性能上的显著成功，RL已迅速发展并应用于各种实际场景，包括游戏、机器人控制和推荐系统等，吸引了不同学科研究人员的广泛关注。

然而，强化学习仍然面临一些需要解决的关键挑战。例如：

1. 数据效率低下：以往的方法大多需要大量的交互数据，但在现实场景中，如医学或医疗保健领域，只有少量记录的数据可用，这主要是由于数据收集过程成本高、不道德或难度大。
2. 缺乏可解释性：现有的方法通常通过深度神经网络来形式化强化学习问题，这些网络属于黑盒模型，以序贯数据作为输入，策略作为输出。它们很难揭示数据背后状态、动作或奖励之间的内在关系，也难以提供关于策略特征的直观理解。这种挑战会阻碍其在工业工程中的实际应用。

有趣的是，因果关系可能在解决强化学习上述挑战方面发挥不可或缺的作用。因果关系主要考虑两个基本问题：

1. 因果发现：揭示因果关系需要哪些经验证据？这种通过证据揭示因果关系的过程简称为因果发现。
2. 因果推断：给定关于某一现象的已接受的因果信息，我们可以从这些信息中得出哪些推断，以及如何得出这些推断？这种推断因果效应或其他感兴趣内容的过程称为因果推断。

因果关系可以使智能体通过因果阶梯进行干预或反事实推理，从而放宽对大量训练数据的要求；它还能够对世界模型进行表征，潜在地为智能体与环境的交互方式提供可解释性。

在过去的几十年里，因果关系和强化学习都在理论和技术上取得了巨大的独立发展，但它们可以相互协调地整合。Bareinboim开发了一个统一的框架，称为因果强化学习，将它们置于相同的概念和理论框架下，并在线提供了相关教程；Lu受当前医疗保健和医学领域发展的启发，将因果关系和强化学习相结合，引入了因果强化学习，并强调了其潜在的适用性。最近，一系列与因果强化学习相关的研究已经提出，因此需要对其发展和应用进行全面的综述。在本文中，我们旨在为读者提供关于因果强化学习的概念、类别和实际问题的良好知识。

尽管已经存在一些相关的综述，但本文考虑的情况不仅限于多智能体或离策略评估。最近，Kaddour等人在arXiv上发布了一篇关于因果机器学习的综述，其中包括一章关于因果强化学习的内容。他们根据因果关系可以带来好处的不同强化学习问题对方法进行了总结，如因果老虎机、基于模型的RL、离策略策略评估等。这种分类方式可能并不完整或全面，遗漏了一些其他的强化学习问题，如多智能体RL。在本文中，我们仅但完整地为这些因果强化学习方法构建了一个分类框架。本文的主要贡献如下：

• 正式定义因果强化学习并首次分类：我们正式定义了因果强化学习，并从因果关系的角度首次将现有方法分为两类。第一类基于先验因果信息，这类方法通常假设关于环境或任务的因果结构是由专家预先给定的；第二类基于未知因果信息，这类方法需要为策略学习相关的因果信息。
• 全面综述现有方法：我们对每一类当前的方法进行了全面的综述，并进行了系统的描述（和示意图）。对于第一类，CRL方法在策略学习中充分利用先验因果信息，以提高样本效率、因果解释能力或泛化能力。对于因果信息未知的CRL，这些方法通常包含两个阶段：因果信息学习和策略学习，这两个阶段可以迭代或交替进行。
• 分析应用、评估指标、开源资源和未来方向：我们进一步分析和讨论了CRL的应用、评估指标、开源资源以及未来的发展方向。

二、预备知识

在这里，我们给出因果关系和强化学习中的基本定义和概念，这些将在本文中贯穿使用。

A. 因果关系

对于因果关系，我们首先定义符号和假设，然后从因果发现和因果推断的角度介绍一般方法。前者解决从纯观测数据中识别因果结构的问题，它利用统计特性来揭示感兴趣变量之间的因果关系；而后者旨在当因果关系完全或部分已知时，推断因果效应或其他统计感兴趣的内容。

定义和假设

• 定义1（结构因果模型（SCMs））：给定一组方程，如果每个方程代表一个自主机制，并且每个机制仅确定一个不同变量的值，则该模型称为结构因果模型，简称因果模型。
  $$x_i=f_i(p{a}_i,u_i),i=1,...,n$$
  其中，$x_i$ 和 $u_i$ 分别是第 $i$ 个随机变量及其误差变量。$f_i$ 表示生成机制，$p{a}_i$ 是 $x_i$ 的父变量集合，即 $x_i$ 的直接原因。
  给定一个包含两个随机变量的SCM，满足：
  $$x_1=u_1,x_2=f_2(x_1,u_2)$$
  则 $x_1\to x_2$ 被称为因果图。这里，$x_1$ 是 $x_2$ 的原因或父节点。每个因果模型都可以与一个有向图相关联。
• 定义2（鲁宾因果模型）：鲁宾因果模型涉及一个观测数据集 {Yi,Ti,Xi}\{ Y_i, T_i, X_i \}{Yi​,Ti​,Xi​}，其中 $Y_i$ 表示第 $i$ 个单元的潜在结果；Ti∈{0,1}T_i \in \{ 0, 1 \}Ti​∈{0,1} 是一个指示变量，表示是否接受处理；$X_i$ 是一组协变量。
  鲁宾因果模型也被称为潜在结果框架或内曼 - 鲁宾潜在结果。由于单个单元不能同时接受不同的处理，而只能一次接受一种处理，因此不可能同时获得两个潜在结果，必须估计缺失的那个。通过潜在结果，鲁宾因果模型旨在估计处理效应。
• 定义3（处理效应）：处理效应可以在总体、处理组、子组和个体水平上进行评估。
  • 总体平均处理效应（ATE）：定义为
    $$ATE=E[Y(T=1)-Y(T=0)]$$
    其中，$Y(T=1)$ 和 $Y(T=0)$ 分别表示接受和未接受处理的潜在结果。
  • 处理组平均处理效应（ATT）：定义为
    $$ATT=E[Y(T=1)|T=1]-E[Y(T=0)|T=1]$$
    其中，$Y(T=1)|T=1$ 和 $Y(T=0)|T=1$ 分别表示处理组中接受和未接受处理的潜在结果。
  • 条件平均处理效应（CATE）：定义为
    $$CATE=E[Y(T=1)|X=x]-E[Y(T=0)|X=x]$$
    其中，$Y(T=1)|X=x$ 和 $Y(T=0)|X=x$ 分别表示子组 $X=x$ 中接受和未接受处理的潜在结果。
  • 个体处理效应（ITE）：定义为
    $$IT{E}_i=Y_i(T=1)-Y_i(T=0)$$
    其中，$Y_i(T=1)$ 和 $Y_i(T=0)$ 分别表示第 $i$ 个单元接受和未接受处理的潜在结果。
• 定义4（混杂因素）：因果图中的混杂因素是两个观测变量的未观测到的直接共同原因。特别是，潜在结果框架中的混杂因素是那些既影响处理又影响结果的变量。
• 定义5（工具变量（IVs））：如果一个变量 $Z$ 满足以下两个条件，则它是相对于 $(T,Y)$ 对的工具变量：
  1. $Z$ 与所有不通过 $T$ 中介而影响结果 $Y$ 的变量（包括误差项）独立。
  2. $Z$ 与处理 $T$ 不独立。
• 定义6（条件独立性）：设 X={x1,...,xn}\mathbf{X} = \{ x_1, ..., x_n \}X={x1​,...,xn​} 是一个有限变量集。设 $P(\cdot )$ 是 $\mathbf{X}$ 中变量的联合概率函数，$Y$、$W$、$Z$ 表示 $\mathbf{X}$ 中任意三个变量子集。如果
  $$P(y|w,z)=P(y|z),\text{ 当 }P(w,z)>0$$
  则称集合 $\mathbf{Y}$ 和 $\mathbf{W}$ 在给定 $\mathbf{Z}$ 的条件下是独立的，记为 $\mathbf{Y}\perp \mathbf{W}|\mathbf{Z}$。
  换句话说，一旦我们知道 $Z$ 的值，学习 $W$ 的值不会为 $Y$ 提供额外的信息。
  最广泛应用的条件独立性测试工具之一是基于核的条件独立性测试（KCI - 测试），其测试统计量是从核矩阵计算得出的，用于表征再生核希尔伯特空间中函数的不相关性。
• 定义7（后门准则）：在有向无环图（DAG）中，变量集 $\mathbf{Z}$ 相对于有序变量对 $(x_i,x_j)$ 满足后门准则，如果：
  1. $\mathbf{Z}$ 中没有节点是 $x_i$ 的后代。
  2. $\mathbf{Z}$ 阻断了 $x_i$ 和 $x_j$ 之间所有包含指向 $x_i$ 的箭头的路径。
     类似地，如果 $\mathbf{Y}$ 和 $\mathbf{W}$ 是 DAG 中两个不相交的节点子集，则称 $\mathbf{Z}$ 相对于 $(\mathbf{Y},\mathbf{W})$ 满足后门准则，如果它相对于任何满足 $x_i\in \mathbf{Y}$ 和 $x_j\in \mathbf{W}$ 的 $(x_i,x_j)$ 对都满足该准则。
• 定义8（前门准则）：变量集 $\mathbf{Z}$ 相对于有序变量对 $(x_i,x_j)$ 满足前门准则，如果：
  1. $\mathbf{Z}$ 拦截了从 $x_i$ 到 $x_j$ 的所有有向路径。
  2. 从 $x_i$ 到 $\mathbf{Z}$ 没有后门路径。
  3. 从 $\mathbf{Z}$ 到 $x_j$ 的所有后门路径都被 $x_i$ 阻断。

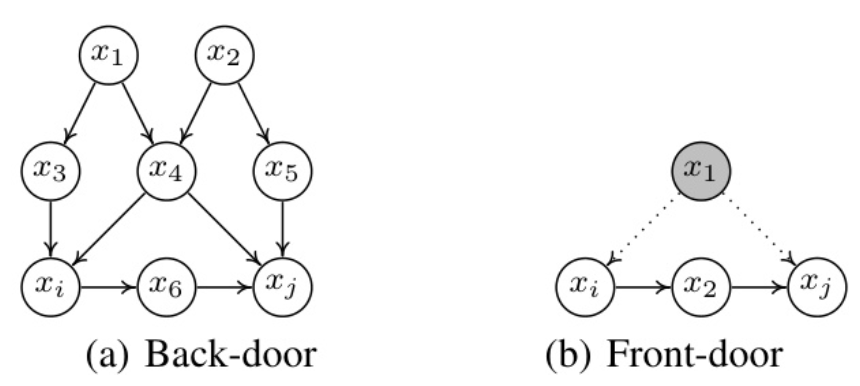
图1是后门和前门准则的示例说明，其中未阴影的变量是观测到的，而阴影的变量是未观测到的。（b）中的 $x_1$ 是一个潜在的混杂因素。

后门和前门准则是两个简单的图形测试，用于判断变量集 $\mathbf{Z}\subseteq \mathbf{X}$ 是否足以估计因果效应 $P(x_j|x_i)$。如图1所示，变量集 Z={x3,x4}\mathbf{Z} = \{ x_3, x_4 \}Z={x3​,x4​} 满足后门准则，而 Z={x2}\mathbf{Z} = \{ x_2 \}Z={x2​} 满足前门准则。

因果阶梯引起了许多不同领域研究人员的广泛关注。它指出因果关系有三种类型的层次，即关联、干预和反事实。它们对应于与数据生成过程的不同交互方式：

• 定义9（关联（观察））：设 $\mathbf{Y}$ 和 $\mathbf{Z}$ 是 $\mathbf{X}$ 中的两个变量子集。关联语句 “如果 $\mathbf{Y}$ 的值为 $y$，那么 $\mathbf{Z}$ 的值是多少？” 被解释为 $\mathbf{Z}$ 对 $\mathbf{Y}$ 的因果效应，记为 $P(\mathbf{Z}|\mathbf{Y})$。
• 定义10（干预（行动））：设 $\mathbf{Y}$ 和 $\mathbf{Z}$ 是 $\mathbf{X}$ 中的两个变量子集。干预语句 “如果将 $\mathbf{Y}$ 的值设置为 $y$，那么 $\mathbf{Z}$ 的值会是多少？” 被解释为 $\mathbf{Z}$ 对行动 $do(\mathbf{Y}=y)$ 的因果效应，记为 $P(\mathbf{Z}|do(\mathbf{Y}=y))$。
• 定义11（反事实（想象））：设 $\mathbf{Y}$ 和 $\mathbf{Z}$ 是 $\mathbf{X}$ 中的两个变量子集。反事实语句 “如果 $\mathbf{Y}$ 的值曾经是 $y$，那么 $\mathbf{Z}$ 的值会是多少？” 被解释为 $\mathbf{Z}$ 对行动 $do(\mathbf{Y}=y)$ 的潜在响应，它是通过求解 $\mathbf{Z}$ 的方程集 $f_{\mathbf{Z}}(\cdot )$ 得到的，记为 $P({\mathbf{Z}}_Y|y)$。

以下假设1 - 3通常用于因果发现以找到因果结构：

• 假设1（因果马尔可夫假设）：概率总体分布 $P$ 相对于因果图（DAG）是马尔可夫的充要条件是，每个变量在给定其父母的条件下与所有非后代变量独立。
• 假设2（因果忠实性假设）：总体中的概率分布 $P$ 没有额外的条件独立关系，这些关系不是由因果图的 $d$ - 分离所蕴含的。
• 假设3（因果充分性假设）：对于变量集 $\mathbf{X}$，不存在导致 $\mathbf{X}$ 中多个变量的隐藏共同原因，即潜在混杂因素。

假设4 - 6通常用于因果推断以估计处理效应：

• 假设4（稳定单位处理值假设）：任何给定单元的潜在结果不会随分配给其他单元的处理而变化，并且对于每个单元，不存在不同版本的处理导致不同的潜在结果。
• 假设5（可忽略性）：给定背景协变量 $X$，处理分配 $T$ 与潜在结果独立，即 $T\perp Y(T=0),Y(T=1)|X$。
• 假设6（正性）：给定 $X$ 的任何值，处理分配 $T$ 不是确定性的：
  $$P(T=t|X=x)>0,\forall t\text{ 和 }x$$

因果发现

从数据中识别因果结构的传统方法是使用干预、随机实验或对照实验，但在许多情况下，这些方法成本太高、耗时太长，甚至不道德。因此，从纯观测数据中揭示因果信息，即因果发现，引起了广泛关注。大致有两种经典的因果发现方法：基于约束的方法和基于得分的方法。

20世纪90年代初，基于约束的方法利用条件独立关系在适当的假设下恢复观测变量之间的潜在因果结构。这些方法包括PC算法和快速因果推断（FCI）算法，它们允许不同类型的数据分布和因果关系，并能给出渐近正确的结果。PC算法假设潜在因果图中没有潜在混杂因素，而FCI算法能够处理存在潜在混杂因素的情况。然而，它们恢复的是一个因果结构的等价类，其中包含多个蕴含相同条件独立关系的有向无环图（DAG）。

另一方面，基于得分的方法试图通过优化一个适当定义的得分函数来搜索等价类，例如贝叶斯信息准则（BIC）、广义得分函数等。它们输出一个或多个得分最高的候选因果图。一个著名的两阶段搜索过程是贪婪等价搜索（GES），它直接在等价类空间中进行搜索。

为了区分等价类中的不同DAG并获得因果结构的唯一可识别性，基于约束的功能因果模型的算法应运而生。这些算法假设了数据生成机制，包括模型类别或噪声分布：效应变量是直接原因和独立噪声的函数，如方程（1）所示，其中原因 $p{a}_i$ 与噪声 $u_i$ 独立。这使得因果结构具有唯一可识别性，因为模型假设（如 $p{a}_i$ 和 $u_i$ 之间的独立性）仅在真实因果方向上成立，而在错误方向上会被违反。这些约束的功能因果模型的例子包括线性非高斯无环模型（LiNGAM）、加性噪声模型（ANM）、后非线性模型（PNL）等。

此外，还有许多重要且具有挑战性的研究主题引起了研究人员的兴趣。例如，有人对时间序列数据的算法感兴趣，这些算法包括tsFCI、SVARFCI、tsLiNGAM、LPCMCI等。特别是，格兰杰因果关系允许在没有瞬时效应或潜在混杂因素的情况下推断时间序列的因果结构，它以前常用于经济学预测。基于异构/非平稳数据的约束因果发现（CD - NOD）适用于潜在生成过程在不同领域或时间上发生变化的情况，它可以揭示因果骨架和方向，并估计变化的因果模块的低维表示。

因果推断

从数据中学习因果效应的最有效方法也是进行随机实验，以比较对照组和处理组之间的差异。然而，由于成本高、实际操作和伦理问题，其应用受到很大限制。因此，从观测数据中估计处理效应越来越受到关注。

从观测数据进行因果推断的困难在于存在混杂变量，这会导致：

1. 处理组和对照组之间的选择偏差。
2. 虚假效应。

这些问题会降低处理结果估计的性能。为了解决虚假效应问题，一种代表性的方法是分层，也称为子分类或分块。其思想是将整个群体划分为同质的子群体，每个子群体中的处理组和对照组在某些协变量上具有相似的特征。

为了克服选择偏差挑战，一般有两种类型的因果推断方法：

1. 创建伪群体：这类方法旨在创建一个与处理组近似一致的伪群体，包括样本重加权方法、匹配方法、基于树的方法和基于表示的方法等。
2. 元学习方法：这类方法首先在观测数据上训练结果估计模型，然后纠正由选择偏差引起的估计偏差。

上述因果推断方法依赖于假设4 - 6的满足。在实践中，这些假设可能并不总是成立。例如，当存在潜在混杂因素时，假设5不成立，即 $T/\perp Y(T=0),Y(T=1)|X$。在这种情况下，一种解决方案是应用敏感性分析，以研究推断如何随给定未测量混杂因素的不同程度而变化。敏感性分析通常通过不可识别分布 $P(Y(T=t)|T=1-t,X)$ 和可识别分布 $P(Y(T=t)|T=t,X)$ 之间的差异来量化未测量的混杂或隐藏偏差：
$$
\begin{array}{c}
c_t(X) = E(Y(T = t) | T = 1 - t, X) \

• E(Y(T = t) | T = t, X)
  \end{array}
  $$
  通过指定 $c_t(X)$ 的边界，可以得到结果期望 $E(Y(T=t))$ 的边界，形式为不可识别的选择偏差。另一种可能的解决方案是充分利用工具变量（IV）回归方法和近端因果学习（PCL）方法。这些方法用于预测处理或政策的因果效应，即使存在潜在混杂因素。值得注意的是，PCL的直觉是构建两个条件独立的代理变量，以反映未观测到的混杂因素的影响。图2展示了工具变量和代理变量的示例。

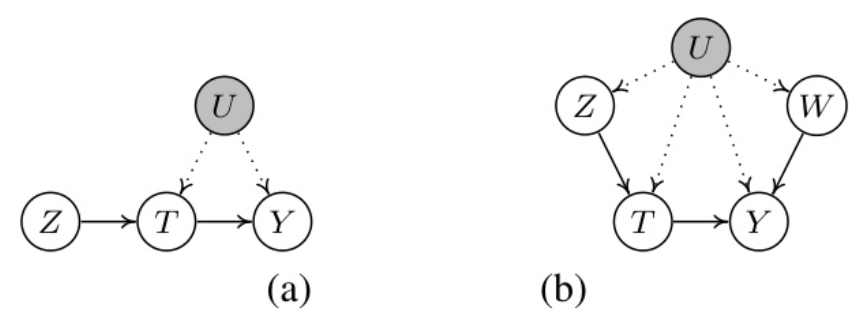
图2为工具变量和代理变量的示例说明，其中未阴影的变量是观测到的，而阴影的变量 $U$ 是未观测到的。$T$ 表示处理，$Y$ 表示结果。（a）中，$Z$ 是一个工具变量；（b）中，{Z,W}\{ Z, W \}{Z,W} 是代理变量。

B. 强化学习

在本节中，我们首先根据标准教科书的定义介绍强化学习的特点和基本概念，然后从无模型和基于模型的强化学习方法的角度给出基线，这意味着是否利用世界模型（包括动态和奖励函数）。

定义

与监督学习和无监督学习相比，强化学习具有两个关键组件的优势：最优控制和试错学习。基于最优控制问题，理查德·贝尔曼开发了一种动态规划方法，使用带有系统状态信息的价值函数进行数学形式化。这种价值函数被称为贝尔曼方程，如下所示：
$$V(s_t)=r(s_t)+\gamma \sum _{s_{t+1}\in S}P(s_{t+1}|s_t,a_t)\cdot V(s_{t+1})$$
其中，$V(s_t)$ 是时间 $t$ 时状态 $s_t$ 的价值函数，$s_{t+1}$ 是下一个状态，$r(s_t)$ 是奖励函数，$\gamma$ 是折扣因子。$P(s_{t+1}|s_t,a_t)$ 是给定当前状态 $s_t$ 和动作 $a_t$ 时 $s_{t+1}$ 的转移概率。

通过交互进行学习是强化学习的本质。智能体在状态 $s_t$ 下采取动作 $a_t$ 与环境进行交互，一旦观察到下一个状态 $s_{t+1}$ 和奖励 $r(s_t)$，它需要调整策略以追求最优回报。这种试错学习机制源于动物心理学，意味着导致良好结果的动作可能会被重复，而导致不良结果的动作会被抑制。

强化学习在不同的设置中解决从可用信息中学习策略的问题，包括多臂老虎机（MAB）、上下文老虎机（CB）、马尔可夫决策过程（MDP）、部分可观测马尔可夫决策过程（POMDP）、模仿学习（IL）和动态治疗方案（DTR）。

• 定义12（马尔可夫决策过程（MDP））：马尔可夫决策过程定义为一个元组 $\mathcal{M}=(S,\mathcal{A},\mathcal{P},\mathcal{R},\gamma )$，其中 $S$ 是状态集合，$\mathcal{A}$ 是动作集合，$\mathcal{P}$ 表示状态转移概率，定义了 $P(s_{t+1}|s_t,a_t)$ 的分布，$\mathcal{R}:\mathcal{S}\times \mathcal{A}\to \mathbb{R}$ 表示奖励函数，$\gamma \in [0,1]$ 是折扣因子。
• 定义13（部分可观测马尔可夫决策过程（POMDP））：部分可观测马尔可夫决策过程定义为一个元组 $\mathcal{M}=(\mathcal{S},\mathcal{A},\mathcal{O},\mathcal{P},\mathcal{R},\mathcal{E},\gamma )$，其中 $S$、$\mathcal{A}$、$\mathcal{P}$、$\mathcal{R}$、$\gamma$ 与MDP中的符号相同，$\mathcal{O}$ 表示观测集合，$\mathcal{E}$ 是一个发射函数，确定了 $\mathcal{E}(o_t|s_t)$ 的分布。
• 定义14（多臂老虎机（MAB））：$K$ 臂老虎机问题定义为一个元组 $\mathcal{M}=(\mathcal{A},\mathcal{R})$，其中 $\mathcal{A}$ 是玩家在第 $t$ 轮从 $K$ 个臂中选择的臂的集合，$\mathcal{R}$ 是表示奖励的结果变量集合，rt∈{0,1}r_t \in \{ 0, 1 \}rt​∈{0,1}。
  注意，当 $K$ 臂老虎机中存在未观测到的混杂因素时，模型将被建立并替换为 $\mathcal{M}=(\mathcal{A},\mathcal{R},U)$，其中 $U$ 是未观测到的变量，表示臂 $a_t$ 的支付率和选择臂 $a_t$ 的倾向得分。
• 定义15（上下文老虎机（CB））：上下文老虎机定义为一个元组 $\mathcal{M}=(\mathcal{X},\mathcal{A},\mathcal{R})$，其中 $\mathcal{A}$ 和 $\mathcal{R}$ 与MAB中的符号相同，$\mathcal{X}$ 是上下文集合，即观测到的辅助信息。
• 定义16（模仿学习模型（IL））：模仿学习模型定义为一个元组 $\mathcal{M}=(\mathcal{O},\mathcal{T})$，其中 $\mathcal{O}$ 表示可访问的高维观测，$\mathcal{T}$ 表示由专家策略 ${\pi }_D(\cdot |o)$ 生成的轨迹。
• 定义17（动态治疗方案（DTR））：动态治疗方案定义为一系列决策规则 {πT:∀T∈T}\{ \pi_T : \forall T \in \mathbf{T} \}{πT​:∀T∈T}，其中 $\mathbf{T}$ 是治疗集合。每个 ${\pi }_T$ 是一个从治疗和协变量的历史值 $H_T$ 到 $T$ 上概率分布域的映射函数，记为 ${\pi }_T(T|H_T)$。

无模型方法

无模型强化学习方法通常无法直接访问世界模型，而是直接从与环境的交互中纯粹地学习策略，类似于我们在现实世界中的行为方式。流行的方法包括基于策略的方法、基于价值的方法和演员 - 评论家方法。

• 基于策略的方法：直接通过策略参数 $\theta$ 学习最优策略 ${\pi }^{\ast }$，以最大化累积奖励。它们主要利用策略梯度定理来推导 $\theta$。典型的方法包括信赖域策略优化（TRPO）、近端策略优化（PPO）等，这些方法使用函数逼近来自适应或人为调整超参数，以加速方法的收敛。
• 基于价值的方法：智能体更新价值函数以获得最优价值函数 $Q^{\ast }(s,a)$，从而隐式地获得一个策略。Q学习、状态 - 动作 - 奖励 - 状态 - 动作（SARSA）和深度Q网络（DQN）是典型的基于价值的方法。Q学习和SARSA的更新规则涉及学习率 $\alpha$ 和时间差分误差 ${\delta }_t$：
  $$Q(s_t,a_t)=Q(s_t,a_t)+\alpha {\delta }_t$$
  其中，在离策略Q学习中，${\delta }_t=r_{t+1}+\gamma {\max }_{a_{t+1}}Q(s_{t+1},a_{t+1})-Q(s_t,a_t)$；在在策略SARSA中，${\delta }_t=r_{t+1}+\gamma Q(s_{t+1},a_{t+1})-Q(s_t,a_t)$。然而，它只能处理离散的状态和动作空间。DQN使用深度学习用神经网络表示价值或策略，从而能够处理连续的状态或动作。它通过经验回放和冻结目标网络来稳定 $Q$ 函数的学习。DQN的改进包括双重DQN、决斗DQN等。
• 演员 - 评论家方法：结合了基于策略和基于价值方法的优点，其中演员网络源于基于策略的方法，而评论家网络源于基于价值的方法。演员 - 评论家的基本框架由两部分组成：
  1. 演员：根据状态 $s_t$ 输出最佳动作 $a_t$，通过学习最优策略来控制智能体的行为。
  2. 评论家：计算动作的 $Q$ 值，实现对策略的评估。
     典型的方法包括优势演员 - 评论家（A2C）、异步优势演员 - 评论家（A3C）、软演员 - 评论家（SAC）、深度确定性策略梯度（DDPG）等。特别是，SAC引入了最大熵项，以提高智能体的探索能力和随机策略训练过程的稳定性；DDPG应用神经网络在高维和视觉状态空间上操作，它结合了确定性策略梯度（DPG）和DQN方法分别作为演员和评论家，缓解了高偏差和高方差问题。

基于模型的方法

基于模型的强化学习方法主要利用学习到的或给定的世界模型来模拟状态转移，而无需直接与环境交互，从而有效地优化目标策略，类似于人类在脑海中进行想象的方式。我们根据模型的使用方式介绍一些常见的基于模型的强化学习算法，即用于轨迹采样的黑盒模型和用于梯度传播的白盒模型。

• 黑盒模型：当有可用的黑盒模型时，将其应用于策略学习的直接方法是在该模型中进行规划。方法包括蒙特卡罗（MC）、带轨迹采样的概率集成（PETS）、蒙特卡罗树搜索（MCTS）等。MCTS是MC的扩展采样方法，它基本上采用树搜索来确定在每个时间步以高概率转移到高价值状态的动作。它已应用于AlphaGo和AlphaGo Zero中，用于挑战围棋领域的专业人类玩家。

• Dyna - 风格方法：可用的模型还可以用于生成模拟样本，以加速策略学习或价值逼近，这一过程被称为Dyna - 风格方法。也就是说，Dyna中的模型充当经验生成器，以产生增强数据。例如，模型集成信赖域策略优化（ME - TRPO）使用收集的数据学习一组动态模型，并用这些模型生成想象的经验，然后使用TRPO无模型算法在集成模型中用增强数据更新策略；基于模型的策略优化（MBPO）使用策略和学习到的模型对分支轨迹进行采样，并利用SAC进一步用增强数据学习最优策略。

• 白盒模型：当模型是白盒时，即模型的梯度是可用的，可以通过策略网络进行梯度传播，以优化策略参数。典型的方法包括：

  • 基于模型的价值扩展（MBVE）：通过模型展开未来状态 - 动作对，并使用无模型方法估计这些未来对的价值，从而扩展价值函数的视野。
  • PILCO：一种概率性的基于模型的强化学习方法，它明确地考虑了模型的不确定性，并使用解析方法计算策略梯度。
  • 基于模型的深度强化学习（MBRL）：结合深度学习和基于模型的方法，直接从高维输入（如图像）学习动态模型，并利用这些模型优化策略。

基于模型的方法通常具有较高的数据效率，因为它们可以利用模型预测来减少与环境的交互次数。然而，它们的性能高度依赖于模型的准确性，不准确的模型可能会导致策略优化的偏差。

三、因果强化学习方法分类

在本节中，我们将现有因果强化学习（CRL）方法分为两类：基于先验因果信息的CRL和因果信息未知的CRL。这种分类基于是否预先给定因果结构或因果效应等因果关系信息。对于每一类，我们将从不同的强化学习模型形式化角度进行详细分析。

A. 基于先验因果信息的CRL

这类方法假设关于环境或任务的因果结构是由专家预先给定的，或者可以从领域知识中直接获得。在这种情况下，CRL方法在策略学习中充分利用这些先验因果信息，以提高样本效率、因果解释能力或泛化能力。

1. 因果马尔可夫决策过程（CMDP）

因果马尔可夫决策过程是MDP的扩展，它明确地将因果结构纳入考虑。在CMDP中，状态转移和奖励函数不仅依赖于当前状态和动作，还依赖于潜在的因果机制。

• 因果状态抽象：CMDP允许通过因果结构进行状态抽象，将高维状态空间压缩到因果相关的变量子集，从而简化决策过程。例如，通过识别因果图中的因果充分变量集，可以忽略那些与决策无关的变量，减少状态空间的维度。
• 因果干预策略学习：在CMDP中，可以利用因果干预来学习更鲁棒的策略。通过模拟干预（如do - 算子），智能体可以评估不同动作对环境的因果效应，而不仅仅依赖于观察到的关联关系。这在存在混杂因素的环境中尤为有用。

2. 因果部分可观测马尔可夫决策过程（CPOMDP）

CPOMDP是POMDP的因果扩展，它处理部分可观测环境中的决策问题，并利用因果结构来提高状态估计和策略学习的性能。

• 因果隐变量建模：在CPOMDP中，隐变量可以通过因果结构进行建模。因果图可以帮助识别哪些隐变量对观测和决策有直接影响，从而更有效地估计隐藏状态。
• 因果感知的信念更新：传统POMDP中的信念更新仅基于观测的似然性，而CPOMDP中的信念更新可以结合因果知识，考虑观测的因果来源，从而提高信念状态的准确性。

3. 因果多臂老虎机（CMAB）

因果多臂老虎机是MAB的扩展，它考虑了动作选择和奖励之间的因果关系，而不仅仅是统计关联。

• 因果效应估计：在CMAB中，目标是估计每个臂（动作）的因果效应，而不是简单的平均奖励。通过考虑潜在的混杂因素，可以更准确地估计每个动作的真实因果效应。
• 因果上下文利用：当存在上下文信息时，因果多臂老虎机可以利用因果结构来识别哪些上下文变量对奖励有因果影响，从而更有效地利用上下文信息进行决策。

4. 因果动态治疗方案（CDTR）

CDTR是DTR的因果扩展，它在序贯治疗决策中考虑因果效应，特别适用于医疗保健和个性化治疗等领域。

• 因果效应最大化：CDTR的目标是找到一个治疗策略，最大化长期因果效应，而不仅仅是短期奖励。这需要考虑治疗决策之间的因果相互作用和长期影响。
• 反事实推理：CDTR可以利用反事实推理来评估不同治疗方案的潜在结果，即使这些方案在历史数据中没有被观察到。这对于个性化医疗决策尤为重要。

B. 因果信息未知的CRL

这类方法需要为策略学习相关的因果信息，通常包含两个阶段：因果信息学习和策略学习，这两个阶段可以迭代或交替进行。

1. 因果发现与强化学习结合

这种方法首先从数据中发现因果结构，然后利用发现的因果结构指导策略学习。

• 联合学习框架：一些方法提出了联合学习框架，同时优化因果发现和策略学习。例如，通过设计一个共享表示，使得因果结构学习和策略优化可以相互促进。
• 因果正则化：在策略学习过程中，可以引入因果正则化项，鼓励策略关注因果相关的变量，而忽略那些仅具有统计关联的变量。这有助于提高策略的泛化能力和可解释性。

2. 因果推断与强化学习结合

这种方法利用因果推断技术来估计因果效应，并将这些估计用于指导策略学习。

• 离线因果强化学习：在离线强化学习设置中，只能访问历史数据，因果推断技术可以用于纠正选择偏差，从而更准确地估计策略价值。例如，利用逆概率加权（IPW）或双重鲁棒（DR）估计器来处理离线数据中的混杂问题。
• 反事实策略评估：因果推断可以用于反事实策略评估，即在不实际执行新策略的情况下，估计其性能。这对于安全关键领域尤为重要，因为在这些领域中进行在线实验可能是危险的或昂贵的。

3. 隐变量因果模型与强化学习

当环境中存在未观测到的混杂因素时，可以使用隐变量因果模型来建模这些潜在变量，并将其纳入强化学习框架。

• 因果变分自编码器：结合变分自编码器和因果模型，可以学习潜在的因果变量表示，并利用这些表示进行更有效的策略学习。
• 因果潜结构发现：通过发现数据中的潜在因果结构，可以揭示环境中的隐藏动态，从而提高策略的性能和鲁棒性。

四、因果强化学习的应用

因果强化学习在许多领域都有潜在的应用价值，特别是在那些需要高数据效率、可解释性或对环境变化具有鲁棒性的场景中。

A. 医疗保健和个性化医疗

在医疗保健领域，CRL可以帮助医生制定个性化治疗方案，考虑患者的个体特征和疾病进展的因果关系。

• 序贯治疗决策：CRL可以用于优化长期治疗策略，考虑不同治疗方案之间的因果相互作用和长期效果。例如，在癌症治疗中，如何根据患者的基因特征和治疗反应动态调整治疗方案。
• 医疗政策评估：通过反事实推理，CRL可以评估不同医疗政策的潜在效果，即使这些政策尚未实施。这对于卫生资源分配和政策制定非常有价值。

B. 机器人控制

在机器人控制中，CRL可以提高机器人的学习效率和对环境变化的适应性。

• 因果环境建模：通过学习环境的因果结构，机器人可以更有效地理解其动作如何影响环境，并做出更明智的决策。
• 迁移学习和泛化：因果知识可以帮助机器人将在一个环境中学习到的技能迁移到其他相关环境中，提高泛化能力。

C. 推荐系统

在推荐系统中，CRL可以解决传统方法中存在的偏差问题，并提供更个性化的推荐。

• 因果效应最大化：通过考虑用户行为的因果效应，推荐系统可以提供更符合用户长期利益的推荐，而不仅仅是短期点击。
• 消除选择偏差：在推荐系统中，用户的交互数据通常受到选择偏差的影响。CRL可以利用因果推断技术来纠正这种偏差，提高推荐的准确性。

D. 自动驾驶

在自动驾驶领域，CRL可以提高自动驾驶系统的安全性和可靠性。

• 因果风险评估：通过建模驾驶决策和事故风险之间的因果关系，自动驾驶系统可以更准确地评估潜在风险，并采取相应的预防措施。
• 反事实测试：CRL可以用于反事实测试，即在模拟环境中评估不同驾驶决策的潜在后果，从而改进自动驾驶算法。

E. 自然语言处理

在自然语言处理中，CRL可以用于构建更具解释性和鲁棒性的语言模型。

• 因果关系理解：通过学习文本中的因果关系，语言模型可以更好地理解文本的含义，并生成更合理的回复。
• 可控文本生成：CRL可以用于控制文本生成过程，例如通过干预因果变量来生成具有特定属性的文本。

五、评估指标和开源资源

A. 评估指标

评估CRL方法的性能需要考虑多个方面，包括策略性能、因果结构学习准确性和泛化能力等。

• 策略性能指标：与传统RL类似，可以使用累积奖励、平均回报等指标来评估策略的性能。此外，在离线RL设置中，还可以使用离策略评估（OPE）指标来评估策略在未见过的数据上的性能。
• 因果结构学习指标：对于需要学习因果结构的CRL方法，可以使用结构汉明距离（SHD）、精确率、召回率等指标来评估学习到的因果结构与真实结构的接近程度。
• 因果效应估计指标：在需要估计因果效应的场景中，可以使用均方误差（MSE）、平均绝对误差（MAE）等指标来评估因果效应估计的准确性。
• 泛化能力指标：为了评估CRL方法的泛化能力，可以在不同的环境设置或分布转移下测试策略的性能，例如使用分布外（OOD）泛化指标。

B. 开源资源

随着CRL领域的发展，越来越多的开源工具和数据集可供研究人员使用。

• 因果发现工具：包括PC算法、FCI算法、LiNGAM、ANM等因果发现算法的实现，例如pcalg、causalnex、dowhy等Python库。
• 因果推断工具：提供因果效应估计和反事实推理的工具，例如dowhy、causalml、EconML等Python库。
• 强化学习框架：许多流行的RL框架已经支持因果强化学习，例如OpenAI Gym、Stable Baselines、RLlib等。
• 因果强化学习库：专门为CRL设计的库，例如CausalWorld、CausalRL等，提供了因果环境和CRL算法的实现。
• 数据集：包括合成数据集和真实世界数据集，例如Twins、IHDP、ACIC等因果推断数据集，以及一些专门为CRL设计的数据集。

六、挑战和未来方向

尽管因果强化学习取得了显著进展，但仍面临许多挑战和未解决的问题。

A. 因果结构学习的挑战

• 高维数据：在高维数据场景中，因果结构学习变得更加困难，需要开发更高效的算法。
• 动态因果结构：在许多实际应用中，因果结构可能随时间变化，如何处理动态因果结构是一个重要挑战。
• 隐变量处理：当存在未观测到的混杂因素时，因果结构学习变得更加复杂，需要更先进的隐变量因果模型。

B. 因果与强化学习的深度融合

• 联合优化框架：需要开发更有效的联合优化框架，同时学习因果结构和优化策略，避免两阶段方法中的误差传播问题。
• 因果表示学习：研究如何学习对决策有用的因果表示，而不仅仅是发现因果结构。
• 反事实强化学习：进一步探索反事实推理在强化学习中的应用，例如如何利用反事实经验来提高学习效率。

C. 泛化和鲁棒性

• 分布外泛化：提高CRL方法在分布外环境中的泛化能力，使其能够应对未见过的场景变化。
• 对抗鲁棒性：研究CRL方法对对抗攻击的鲁棒性，特别是在安全关键应用中。

D. 可解释性和透明度

• 因果解释：开发更有效的方法来解释CRL决策的因果依据，提高模型的可解释性。
• 人类可理解的表示：研究如何将因果知识以人类可理解的方式表示，促进人机协作。

E. 应用扩展

• 复杂现实场景：将CRL应用于更复杂的现实场景，如社会科学、经济学、环境科学等。
• 多智能体系统：研究多智能体环境中的因果强化学习，考虑智能体之间的因果交互。

七、结论

因果强化学习是一个新兴且快速发展的领域，它结合了因果关系和强化学习的优势，为解决复杂序贯决策问题提供了新的视角和方法。本文对因果强化学习的研究进行了全面综述，首先介绍了因果关系和强化学习的基本概念，然后根据是否预先给定因果信息将CRL方法分为两类，并从不同的强化学习模型形式化角度进行了详细分析。我们还讨论了CRL的应用领域、评估指标和开源资源，最后提出了该领域面临的挑战和未来发展方向。

随着因果推理和强化学习理论的不断发展，以及计算能力的提升，因果强化学习有望在更多领域取得突破性进展，并为解决实际问题提供更有效的工具。特别是在需要高数据效率、可解释性和鲁棒性的场景中，CRL具有巨大的应用潜力。未来的研究需要进一步探索因果与强化学习的深度融合，开发更高效的算法，并将其应用于更广泛的现实问题。