【C语言】堆的实现（建堆、堆的基本操作、堆排序、TOK问题）详解

原创已于 2025-04-13 22:26:54 修改 · 4.4k 阅读

54 ·

CC 4.0 BY-SA版权

文章标签：

#开发语言 #c语言 #数据结构 #排序算法 #算法 #visual studio #windows

于 2023-12-19 10:46:07 首次发布

数据结构专栏收录该内容

5 篇文章

订阅专栏

本文详细介绍了堆数据结构，包括完全二叉树的概念，大堆和小堆的区别，以及堆的物理结构实现。重点讲解了堆的建立、基本操作（插入、删除、取堆顶和堆排序），并探讨了如何处理TOP-K问题和堆排序的实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一.前言和堆的基本概念

什么是堆？

堆是一种逻辑结构为完全二叉树的数据结构，堆又分为两种，一种是大堆，一种是小堆。

什么是完全二叉树？

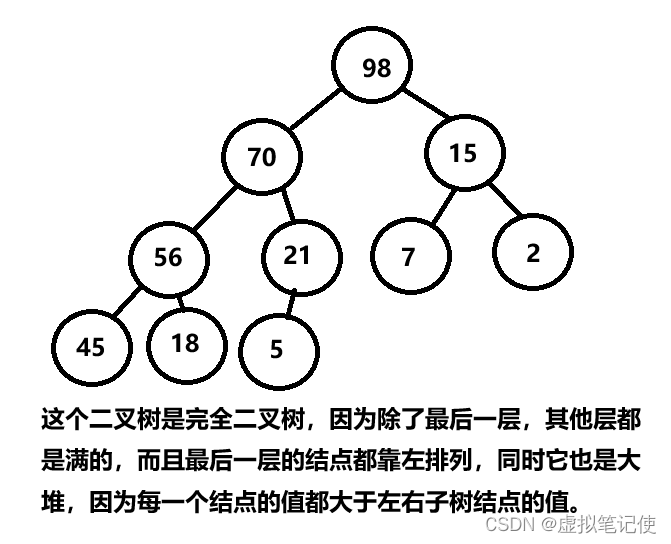
完全二叉树是，除了最后一层外，其他层都是满的，而且最后一层的结点都靠左排列。

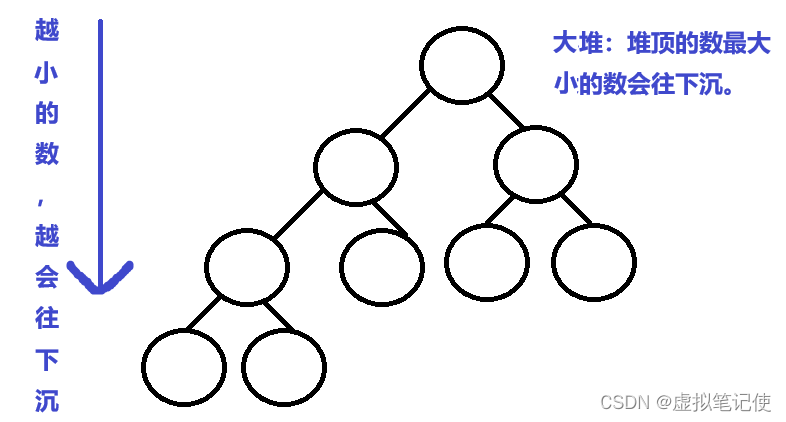
什么是大堆？什么是小堆？

大堆为每个结点的值都大于它的左子树结点和右子树结点的值。

小堆为每个结点的值都小于它的左子树结点和右子树结点的值。

堆有什么用？

堆可以用来选数、排序等且时间复杂度非常低。

1.完全二叉树和大堆如图所示。

2.堆的物理结构

虽然堆的逻辑结构是一棵完全二叉树，但在我们实现它的时候，通常使用数组来实现。即它的物理结构通常是数组。因为使用数组来实现更方便。

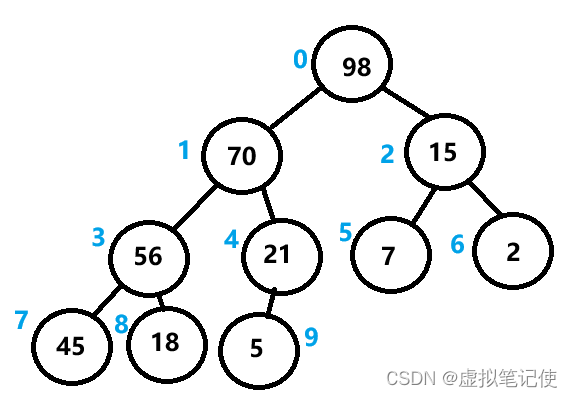
如上图所示，我们从根结点开始依次按照顺序给每个结点标个下标。

结果如下图所示，所以我们只要创建一个数组来存储它的数据即可。

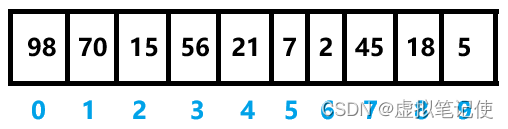
重点！！！

对于一个二叉树而言，知道它的parent结点，可以求出它的左孩子和右孩子，知道它的其中一个孩子，可以求出它的parent结点 。

parent=（child-1）/2

leftchild=parent*2+1

rightchild=parent*2+2

二.堆的建立（以下都已建大堆为例）

堆的初始化通常场景是：给你一个数组，使它变成堆。

那么应该如何实现呢？

既然它的逻辑结构是二叉树，那么我们可以把它分为根、左子树、右子树三个部分来看。

假设一棵树的左子树和右子树已经是大堆了，但是根结点不符合，所以我们需要从根结点开始调整这棵树，使它成为大堆。如下图所示。

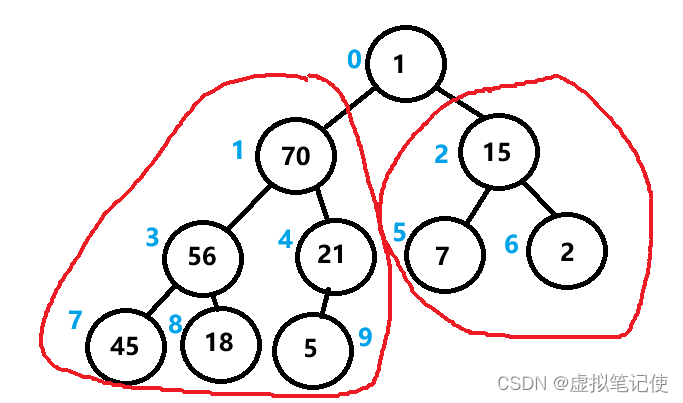
这棵树根结点的左子树和右子树都为大堆，而根结点不符合。这时我们需要写一个向下调整算法，使它成为大堆。

1.向下调整算法（时间复杂度为O（logN））

假设这棵树的根节点的左右子树都已经是大堆，而根结点不符合。

算法思路和流程

①选出根节点的左右结点的较大值

②与根结点比较，如果根节点小，则进行交换

③交换后的结点为新的根，继续向下迭代上述步骤，直到末尾。

如下图所示。

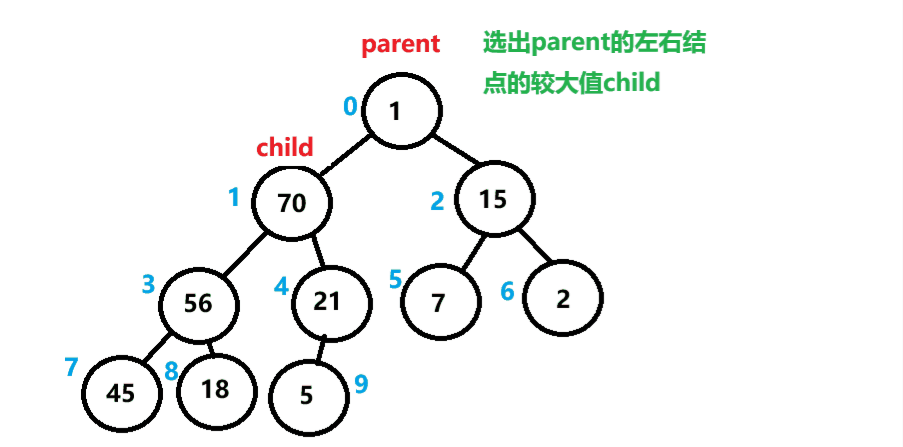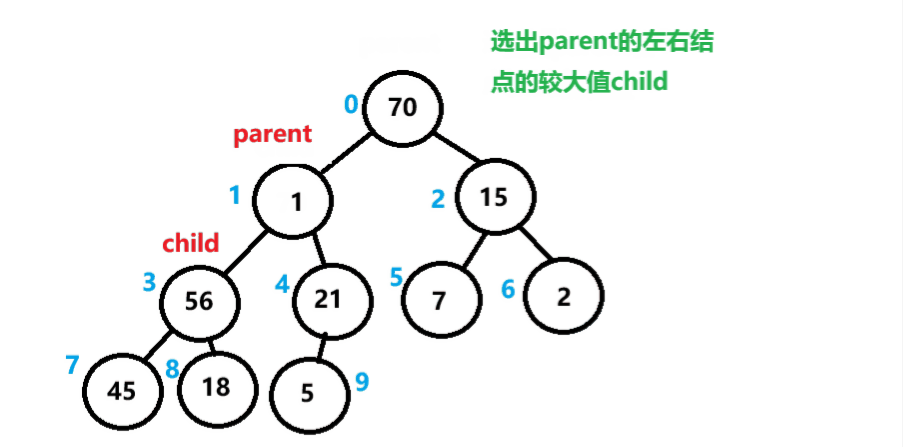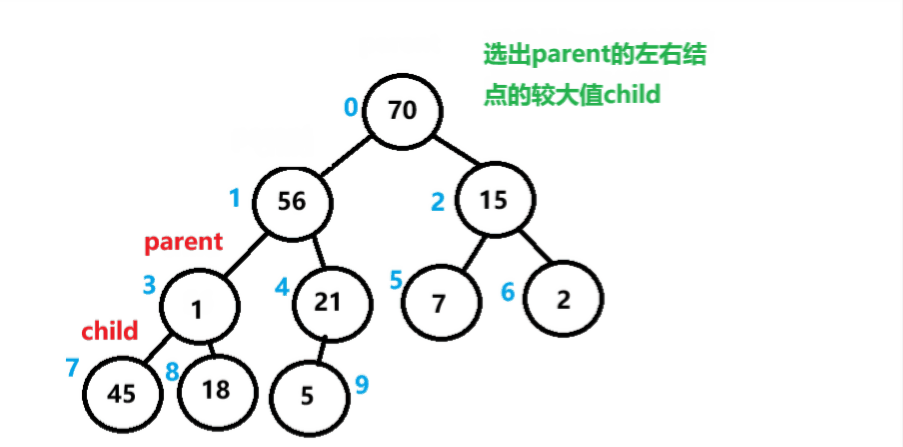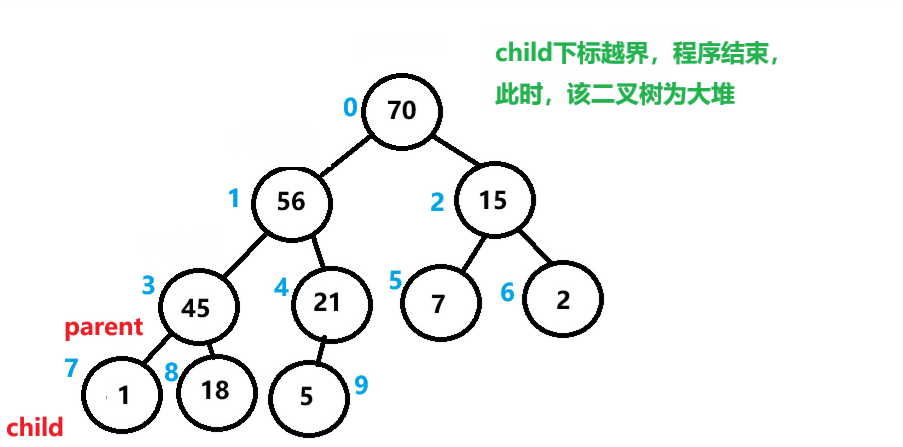
向下调整算法代码实现

void swap(int* num1, int* num2)//交换数组中的两个数
{
	assert(num1 && num2);
	int tmp = *num1;
	*num1 = *num2;
	*num2 = tmp;
}

void AdjustDown(HPData* arr, int root, int n)//向下调整算法  函数 root为从那个根开始调  n为堆数组元素个数  时间复杂度为O（logN）  建大堆
{
	assert(arr);

	int parent = root;
	int child = 2 * parent + 1;//默认左孩子为较大值

	while (child < n)
	{
		if ((child + 1) < n && arr[child + 1] > arr[child])//如果右孩子存在 并且 大于左孩子，则把右孩子给给child
		{
			child++;
		}

		if (arr[child] > arr[parent])//如果孩子大于父节点，则交换
		{
			swap(&arr[parent], &arr[child]);
			parent = child;//孩子结点变为新的父节点
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}

}

2.建堆（时间复杂度为O（n））

通过一趟向下调整算法，使得大堆建立完成。但是我们是先默认根节点的左右子树都为大堆的情况进行建立的，通常一个数组不会那么巧，那么应该怎么办呢？

我们可以对每个结点都进行一次向下调整算法，那么每个结点都是大堆，组成起来总的就是一个大堆。

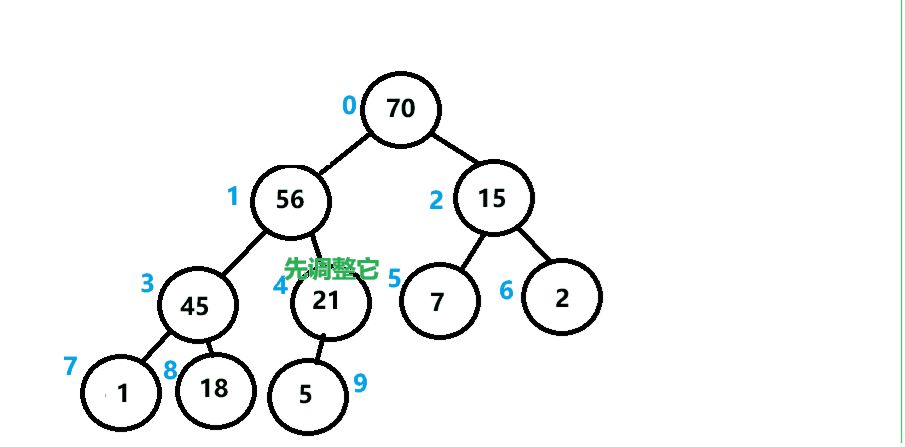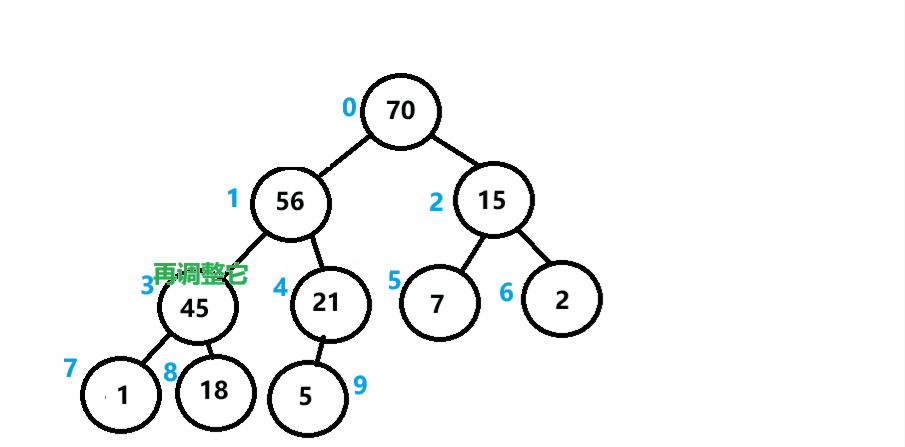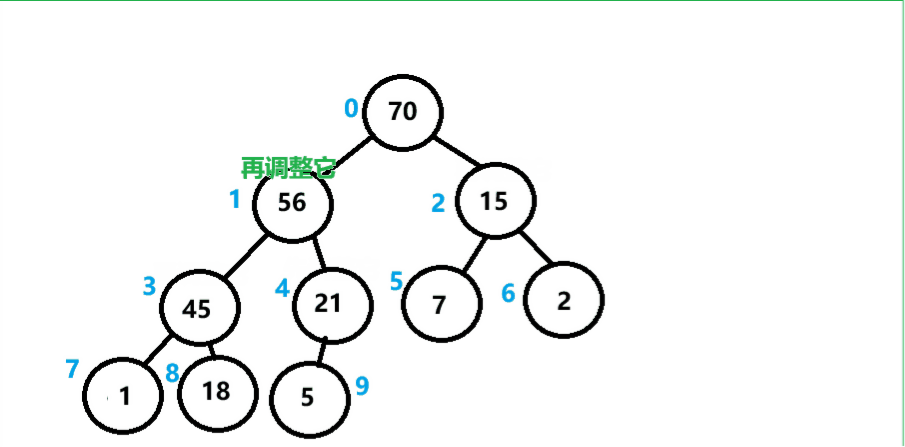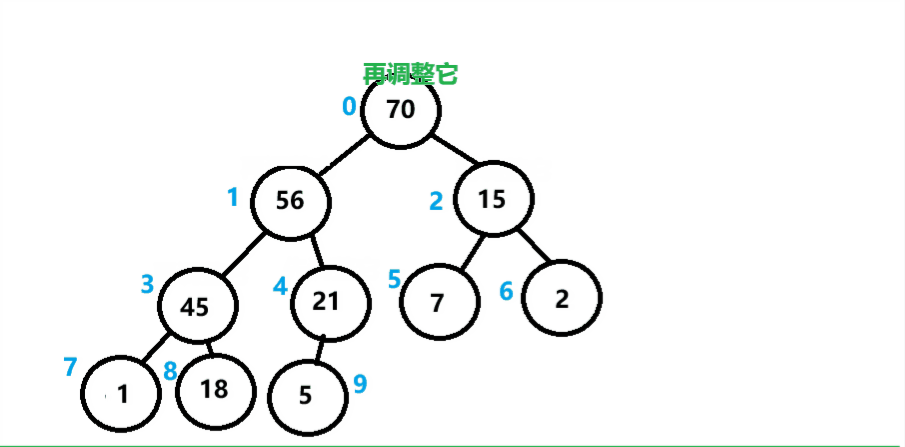
建堆代码实现

	for (int i = (n - 1 -1) / 2; i >= 0; i--)//从最后一个节点的父节点开始向上迭代，令每个子树都为 小堆  i为根节点下标 
	{
		AdjustDown(php->arr, i, n);//向下调整堆
	}

到这里，我们已经对一个数组建成了一个大堆。

三.堆的基本操作（插入一个元素，删除堆顶，取堆顶数据，堆的销毁）

1.在堆中插入一个元素（向上调整算法）

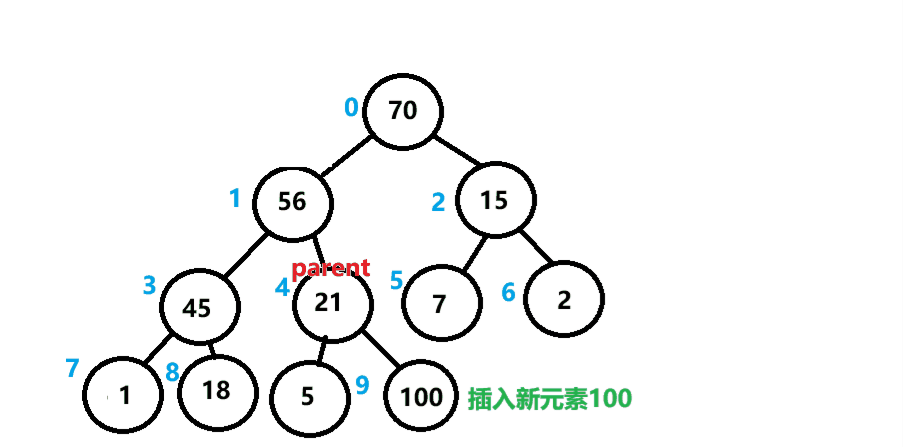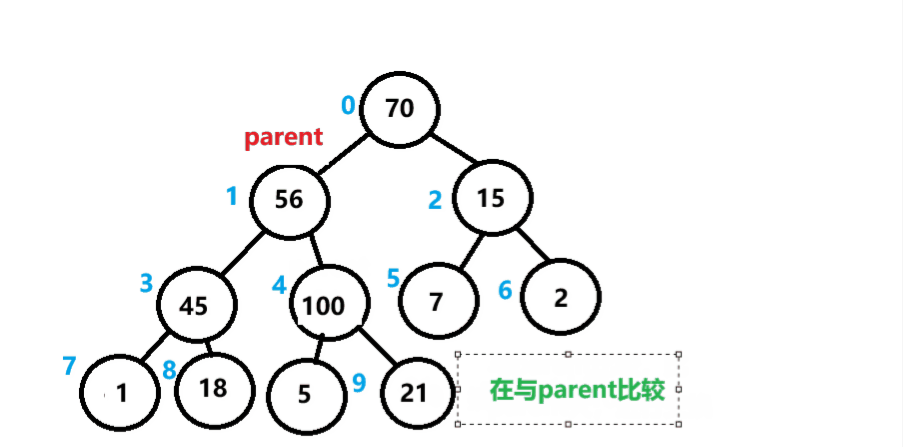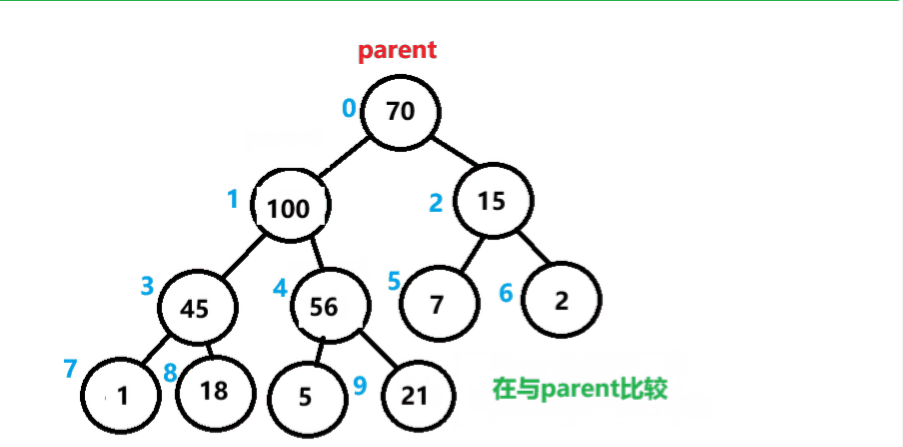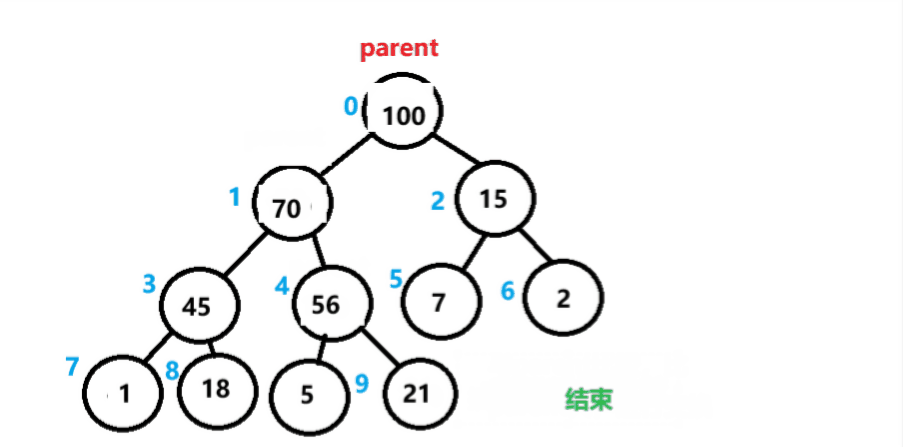
当我们需要在一个已经建好堆的数组中插入一个新元素，通常是在堆的末尾插入，后对堆进行一个向上调整。

与它的父节点比较，如果比父节点大，则进行交换，后依次类推，直到堆顶或中途结束。

向上调整如图所示

向上调整算法代码实现（时间复杂度为O（logN））

void swap(int* num1, int* num2)//交换数组中的两个数
{
	assert(num1 && num2);
	int tmp = *num1;
	*num1 = *num2;
	*num2 = tmp;
}

void AdjustUp(int* arr, int child)//向上调整算法  函数  时间复杂度为 O（logN）  大堆向上调整
{
	int parent = (child - 1) / 2;	

	while (child > 0)
	{
		if (arr[child] > arr[parent])
		{
			swap(&arr[parent], &arr[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

堆的插入代码实现

void HeapPush(int* php, int val)//堆的插入  时间复杂度O（logN）
{
	assert(php);
	if (php->capacity == php->size)//如果数组已满，则增容
	{
		php->capacity *= 2;
		int* tmp = (HPData*)realloc(php->arr, sizeof(HPData) * php->capacity);
		if (tmp == NULL)
		{
			printf("扩容失败\n");
			exit(-1);
		}
		php->arr = tmp;
	}

	php->arr[php->size++] = val;//将新插入的值放到末尾

	AdjustUp(php->arr, (php->size) - 1);//向上调整算法
}

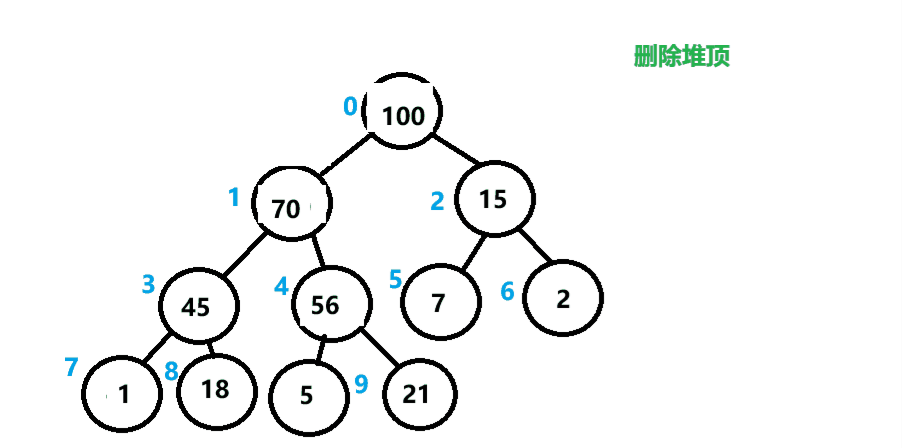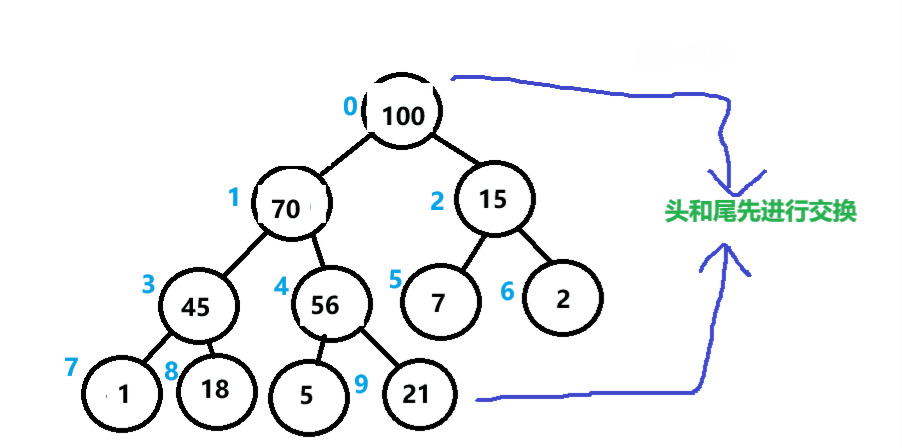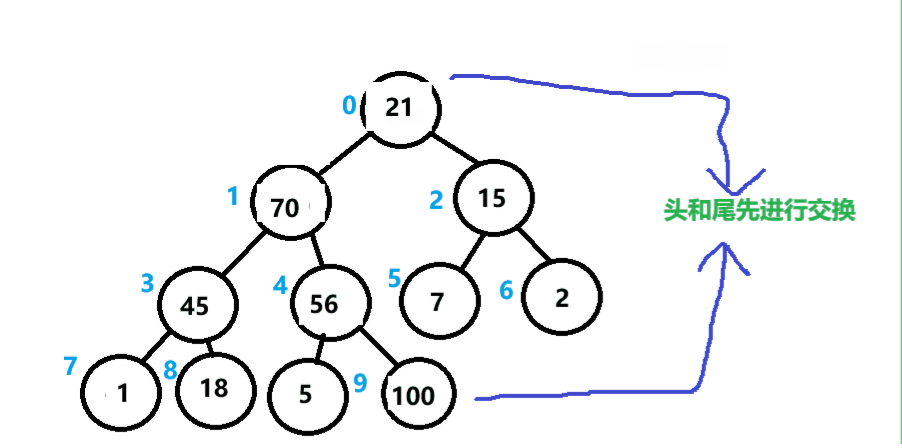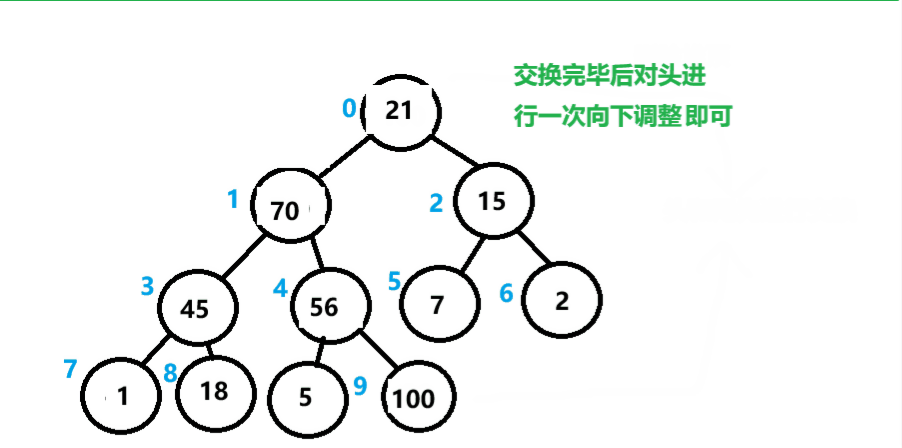
2.删除堆顶

删除堆顶的元素，可以先将头和尾的数据进行交换，然后从根结点开始进行一个向下调整，后令数组的元素个数-1。

如下图所示。

删除堆顶代码实现

void swap(int* num1, int* num2)//交换数组中的两个数
{
	assert(num1 && num2);
	int tmp = *num1;
	*num1 = *num2;
	*num2 = tmp;
}

void HeapPop(int* php)//删除堆顶  时间复杂度为O（logN）
{
	assert(php);
	assert(php->size > 0);
	swap(&php->arr[0], &php->arr[php->size - 1]);
	php->size--;
	AdjustDown(php->arr, 0, php->size);	
}

3.取堆顶数据

取堆顶数据代码实现

HPData HeapTop(int* php)//取堆顶数据
{
	assert(php);
	assert(php->size > 0);
	return php->arr[0];
}

4.堆的销毁

堆的销毁代码实现

void HeapDestory(int* php)//堆的销毁
{
	assert(php);
	free(php->arr);
	php->capacity = php->size = 0;
}

四.堆排序实现（排升序，建大堆为例）（时间复杂度为O（n*logN））

从堆的特点可以看出，大堆的堆顶是堆中的最大值，小堆反之。那么建好一个堆后，可以进行选数，选出堆中的最大值或最小值，那么我们可以进行排序。

1.堆排序流程

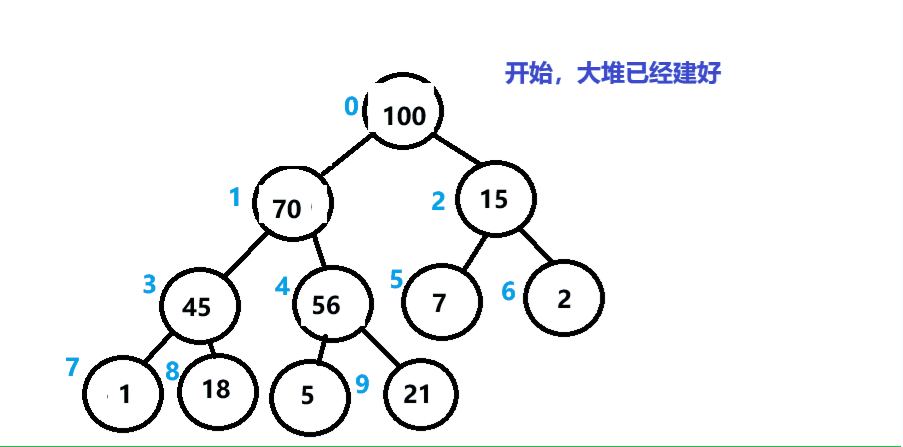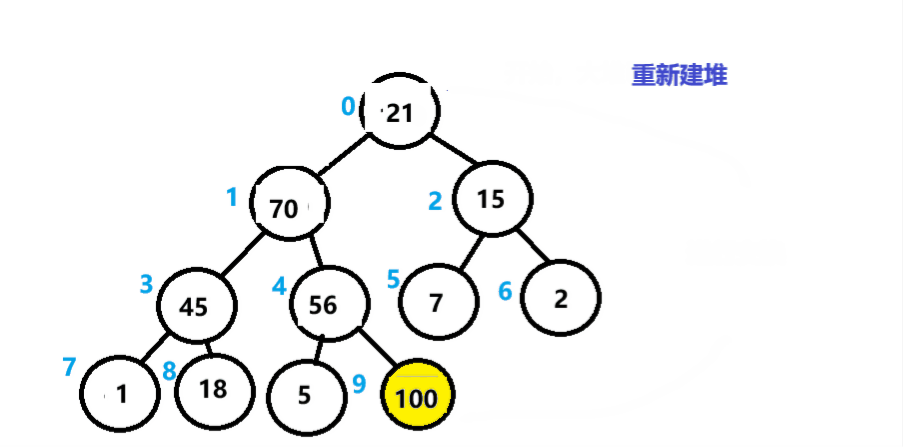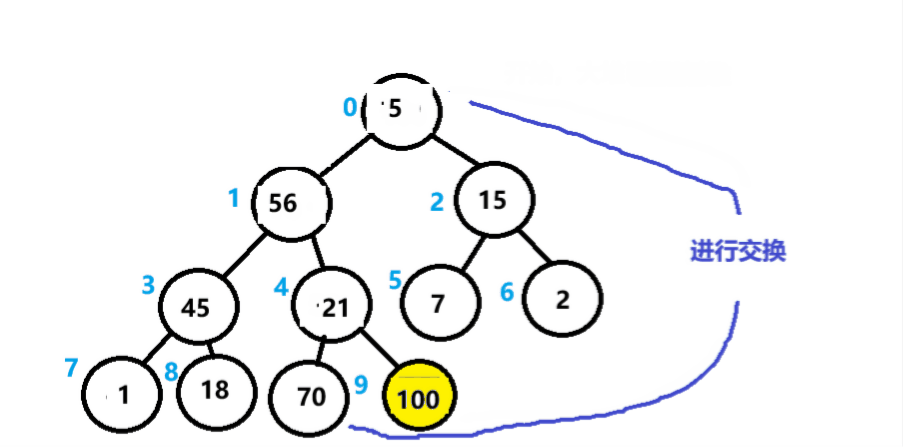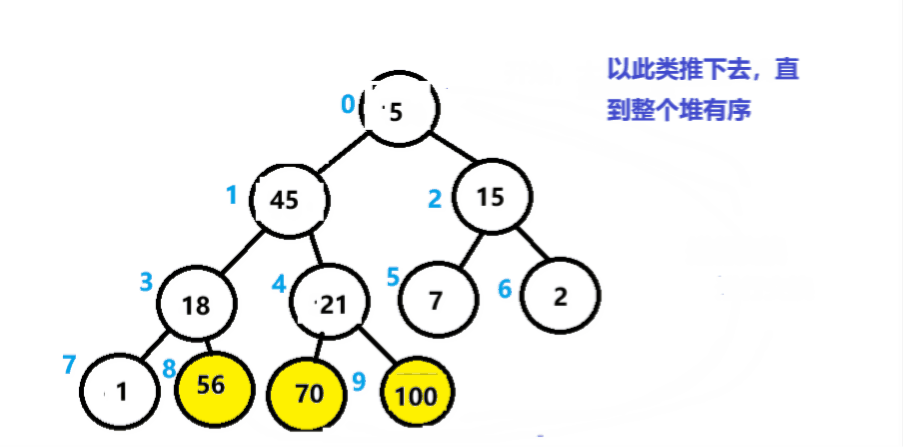
①先对数组进行建大堆。

②将堆的头和尾进行交换。（此时，最大的数到了末尾）

③对剩余的数再进行建大堆。

④再将头和倒数第二个数进行交换。

以此类推。

如下图所示。

堆排序代码实现

void HeapSort(int* a, int sz)//堆排序  时间复杂度为O（n*logN）  sz为元素个数
{
	assert(a);
	for (int i = (sz - 1 - 1)/2; i >= 0; i--)//建堆
	{
		AdjustDown(a, i, sz);
	}

	while (sz)
	{
		swap(&a[0], &a[sz - 1]);
		sz--;
		AdjustDown(a, 0, sz);//重新建大堆
	}

}

五.TOP-K问题

什么是TOP-K问题？

比如说：专业前十名，世界五百强，世界富豪榜等等。

对于TOK-K问题而言，最快能想到的方法就是直接对所有数据进行排序，然后选出前面最大的几个。

但是如果数据量非常大，不能直接全部加载到内存中，这个时候直接对所有数进行排序就不现实了，这个时候，我们需要借助堆来实现。

leetcode刷题链接

面试题 17.14. 最小K个数 - 力扣（LeetCode）

基本思路

选出最大K个数，则建小堆。

选出最小K个数，则建大堆。

为什么选出最小K个数，要建大堆

因为由大堆的性质可知，堆顶是堆中最大的数，堆的下面的数都是比堆的上面的数小。

所以堆顶的数要么是这K个数中最大的，要么是比这K个数都要大，而前面（K-1）个小的数都会沉下去。

解题流程

①选前K个数来建大堆。

②依次将后面没用到数与堆顶比较，如果比堆顶小，则替换堆顶，然后从堆顶进行一次向下调整。

③直到所有数都比较过，此时，对中的K个数就是最小的K个数。

leetcode解题代码

#include<string.h>
#include<stdlib.h>
#include<stdio.h>




void swap(int* sum1,int* sum2)//交换堆中的两个数
{
    int tmp=*sum1;
    *sum1=*sum2;
    *sum2=tmp;
}

void AdjustDown(int* arr,int k,int root)//向下调整算法  k为堆的元素个数  root为从那个根结点开始调
{
    int parent=root;
    int child=parent*2+1;

    while(child<k)
    {
        if((child+1)<k && arr[child+1]>arr[child])
        {
            child++;
        }
        if(arr[child]>arr[parent])
        {
            swap(&arr[child],&arr[parent]);
            parent=child;
            child=parent*2+1;
        }
        else
        {
            break;
        }   
    }

}

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* smallestK(int* arr, int arrSize, int k, int* returnSize)//建大堆
{
    if(k==0)
    {
        *returnSize=0;
        return NULL;
    }
    int* tmp=(int*)malloc(sizeof(int)*k);//开辟k个空间的数组     tmp为大堆
    if(tmp==NULL)
    {
        printf("开辟失败\n");
        exit(-1);
    }

    memcpy(tmp,arr,sizeof(int)*k);//将数组中的元素拷贝到自己开辟的数组中

    for(int i=(k-1-1)/2;i>=0;i--)//建堆
    {
        AdjustDown(tmp,k,i);//向下调整堆
    }

    for(int i=k;i<arrSize;i++)
    {
        if(arr[i]<tmp[0])
        {
            tmp[0]=arr[i];
            AdjustDown(tmp,k,0);
        }
    }
    *returnSize=k;
    return tmp;
}

六.代码清单

1.Heap.h （程序所需要包的头文件，结构体，函数声明等等）

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<assert.h>

typedef int HPData;

typedef struct Heap
{
	HPData* arr;
	int size;
	int capacity;
}Heap;

void HeapInit(Heap* php, HPData* arr, int n);//堆的初始化    参数：堆结构体，给定初始化数组，数组中元素的个数   建堆的时间复炸度为O（n）
void HeapDestory(Heap* php);//堆的销毁

void HeapPush(Heap* php, HPData val);//堆的插入
void HeapPop(Heap* php);//删除堆顶
HPData HeapTop(Heap* php);//取堆顶数据


void AdjustDown(HPData* arr, int root, int n);//向下调整函数   n为堆数组元素个数
void AdjustUp(HPData* arr, int child);//向上调整算法  函数

void swap(HPData* num1, HPData* num2);//交换数组中的两个数
void HeapSort(HPData* a, int sz);//堆排序

2.Heap.c（堆的基本操作）

#include"Heap.h"

void HeapInit(Heap* php, HPData* arr, int n)//堆的初始化  n为数组元素个数   建堆的时间复炸度为O（n）
{
	assert(php && arr);

	php->arr = (HPData*)malloc(sizeof(HPData) * n);
	if (php->arr == NULL)
	{
		printf("开辟失败\n");
		exit(-1);
	}
	php->capacity = php->size = n;

	memcpy(php->arr, arr, sizeof(HPData) * n);

	for (int i = (n - 1 -1) / 2; i >= 0; i--)//从最后一个节点的父节点开始向上迭代，令每个子树都为 小堆  i为根节点下标 
	{
		AdjustDown(php->arr, i, n);//向下调整堆
	}

}

void HeapDestory(Heap* php)//堆的销毁
{
	assert(php);
	free(php->arr);
	php->capacity = php->size = 0;
}

void HeapPush(Heap* php, HPData val)//堆的插入  时间复杂度O（logN）
{
	assert(php);
	if (php->capacity == php->size)
	{
		php->capacity *= 2;
		HPData* tmp = (HPData*)realloc(php->arr, sizeof(HPData) * php->capacity);
		if (tmp == NULL)
		{
			printf("扩容失败\n");
			exit(-1);
		}
		php->arr = tmp;
	}

	php->arr[php->size++] = val;

	AdjustUp(php->arr, (php->size) - 1);
}

void HeapPop(Heap* php)//删除堆顶  时间复杂度为O（logN）
{
	assert(php);
	assert(php->size > 0);
	swap(&php->arr[0], &php->arr[php->size - 1]);
	php->size--;
	AdjustDown(php->arr, 0, php->size);	
}

HPData HeapTop(Heap* php)//取堆顶数据
{
	assert(php);
	assert(php->size > 0);
	return php->arr[0];
}

3.Adjust.c（向下调整算法、向上调整算法和堆排序）

#include"Heap.h"

void swap(HPData* num1, HPData* num2)//交换数组中的两个数
{
	assert(num1 && num2);
	HPData tmp = *num1;
	*num1 = *num2;
	*num2 = tmp;
}

void AdjustDown(HPData* arr, int root, int n)//向下调整算法  函数 root为从那个根开始调  n为堆数组元素个数  时间复杂度为O（logN）  建大堆
{
	assert(arr);

	int parent = root;
	int child = 2 * parent + 1;

	while (child < n)
	{
		if ((child + 1) < n && arr[child + 1] > arr[child])//如果右孩子小于左孩子，则把右孩子给给child
		{
			child++;
		}

		if (arr[child] > arr[parent])//如果孩子小于父节点，则交换
		{
			swap(&arr[parent], &arr[child]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}

}

void AdjustUp(HPData* arr, int child)//向上调整算法  函数  时间复杂度为 O（logN）  大堆向上调整
{
	int parent = (child - 1) / 2;	

	while (child > 0)
	{
		if (arr[child] > arr[parent])
		{
			swap(&arr[parent], &arr[child]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(HPData* a, int sz)//堆排序  时间复杂度为O（n*logN）
{
	assert(a);
	for (int i = (sz - 1 - 1); i >= 0; i--)//建堆
	{
		AdjustDown(a, i, sz);
	}

	while (sz)
	{
		swap(&a[0], &a[sz - 1]);
		sz--;
		AdjustDown(a, 0, sz);
	}

}

4.test.c （测试用例）

#include"Heap.h"

void test1()
{
	HPData a[] = {27,15,19,18,28,34,65,49,25,37};
	Heap S;
	HeapInit(&S, a, sizeof(a) / sizeof(HPData));//初始化堆

	HeapPush(&S, 1);//堆的插入
	HeapPop(&S);//删除堆顶数据
	HeapTop(&S);//取堆顶数据

	HeapSort(a, sizeof(a) / sizeof(int));//堆数组a进行排序

	for (int i = 0; i < S.size; i++)//排完序后进行输出
	{
		printf("%d ", S.arr[i]);
	}

	HeapDestory(&S);//销毁堆

}

int main()
{
	test1();

	return 0;
}