本文探讨了在神经网络中，为何大的输入会导致softmax激活函数的梯度变得极小，从而影响参数更新。通过示例代码展示了随着输入增大，梯度消失的现象。同时，解释了为何在高维空间中，维度的平方根常用于点积的放缩，以保持数值稳定。建议读者直接在原平台查看完整的公式和详细解释，以便更好地理解和讨论问题。
原作者的答案在知乎，由于答案中有大量公式计算符号，无法较好的迁移至优快云。因此选择了粘贴图片的方式进行转载，这种方式可能会为大家的阅读增添不便，希望您能理解。同时如有需要，非常建议大家点击超链接，到知乎中查看原作者的回答，同时也能方便您将自己的疑问或见解评论给原作者，从而更方便地进行后续交流。
1. 为什么比较大的输入会使得softmax的梯度变得很小？
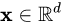，softmax函数将其映射/归一化到一个分布 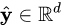。在这个过程中，softmax先用一个自然底数 e 将输入中的元素间差距先“拉大”，然后归一化为一个分布。假设某个输入 中最大的的元素下标是 ，如果输入的数量级变大（每个元素都很大），那么会非常接近1。我们可以用一个小例子来看看 的数量级对输入最大元素对应的预测概率的影响。假定输入 ），我们来看不同量级的 产生的有什么区别。 时， ; 时， ; 时， (计算机精度限制)。我们不妨把 a 在不同取值下，对应的 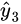的全部绘制出来。代码如下：](https://i-blog.csdnimg.cn/blog_migrate/6b15f8cd4ba9a2eaa34857972a2ad05f.png)
from math import exp
from matplotlib import pyplot as plt
import numpy as np
f = lambda x: exp(x * 2) / (exp(x) + exp(x) + exp(x * 2))
x = np.linspace(0, 100, 100)
y_3 = [f(x_i) for x_i in x]
plt.plot(x, y_3)
plt.show()
输出图像为：
也就是说，在输入的数量级很大时，梯度消失为0，造成参数更新困难。
注： softmax的梯度可以自行推导，网络上也有很多推导可以参考。
2. 维度与点积大小的关系是怎么样的，为什么使用维度的根号来放缩？
针对为什么维度会影响点积的大小，在论文的脚注中其实给出了一点解释
此处补充一下原链接评论区中，“予以初始”的回复评论：
方差越大，说明：
扫一扫
661
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
