文章包含一系列编程挑战，涉及C语言的学习、彩票游戏的模拟以及递归的概念。第一个问题要求根据用户回答构建决策树得出结论编号；第二个问题要求模拟刮刮彩票游戏过程，计算奖金；第三个问题是直接输出关于递归的名言；第四个问题是一个简单的数学计算，求剩余未读的字数；最后一个挑战是整理日期格式，确保年月格式统一。
目录
L1-071 前世档案
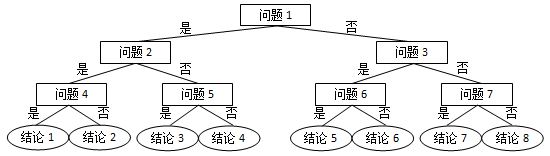
网络世界中时常会遇到这类滑稽的算命小程序，实现原理很简单，随便设计几个问题，根据玩家对每个问题的回答选择一条判断树中的路径（如下图所示），结论就是路径终点对应的那个结点。
现在我们把结论从左到右顺序编号，编号从 1 开始。这里假设回答都是简单的“是”或“否”，又假设回答“是”对应向左的路径，回答“否”对应向右的路径。给定玩家的一系列回答，请你返回其得到的结论的编号。
输入格式：
输入第一行给出两个正整数：N（≤30）为玩家做一次测试要回答的问题数量；M（≤100）为玩家人数。
随后 M 行，每行顺次给出玩家的 N 个回答。这里用 y 代表“是”，用 n 代表“否”。
输出格式：
对每个玩家，在一行中输出其对应的结论的编号。
输入样例：
3 4
yny
nyy
nyn
yyn输出样例：
3
5
6
2
#include <stdio.h>
#include <math.h>
int main()
{
int n,m;
scanf("%d %d",&n,&m);
getchar();
int sum=(int)pow(2,n);
int l=1,r=sum,sums=sum;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
char ch;
scanf("%c",&ch);
sums/=2;
if(ch=='y')
r-=sums;
else
l+=sums;
}
getchar();
printf("%d\n",l);
l=1,r=sum,sums=sum;
}
return 0;
}注意事项：
回答次数决定总结论数，结论区间的左右边界随回答内容改变而改变，并且每回答一次区间长度减少一半。
如有疑问，欢迎提出。
L1-072 刮刮彩票
“刮刮彩票”是一款网络游戏里面的一个小游戏。如图所示：
每次游戏玩家会拿到一张彩票，上面会有 9 个数字，分别为数字 1 到数字 9，数字各不重复，并以 3×3 的“九宫格”形式排布在彩票上。
在游戏开始时能看见一个位置上的数字，其他位置上的数字均不可见。你可以选择三个位置的数字刮开，这样玩家就能看见四个位置上的数字了。最后玩家再从 3 横、3 竖、2 斜共 8 个方向中挑选一个方向，方向上三个数字的和可根据下列表格进行兑奖，获得对应数额的金币。
现在请你写出一个模拟程序，模拟玩家的游戏过程。
输入格式：
输入第一部分给出一张合法的彩票，即用 3 行 3 列给出 0 至 9 的数字。0 表示的是这个位置上的数字初始时就能看见了，而不是彩票上的数字为 0。
第二部给出玩家刮开的三个位置，分为三行，每行按格式 x y 给出玩家刮开的位置的行号和列号（题目中定义左上角的位置为第 1 行、第 1 列。）。数据保证玩家不会重复刮开已刮开的数字。
最后一部分给出玩家选择的方向，即一个整数： 1 至 3 表示选择横向的第一行、第二行、第三行，4 至 6 表示纵向的第一列、第二列、第三列，7、8分别表示左上到右下的主对角线和右上到左下的副对角线。
输出格式：
对于每一个刮开的操作，在一行中输出玩家能看到的数字。最后对于选择的方向，在一行中输出玩家获得的金币数量。
输入样例：
1 2 3
4 5 6
7 8 0
1 1
2 2
2 3
7输出样例：
1
5
6
180
#include <stdio.h>
int main()
{
int col, row;
int num[3][3];
int temp[10];
int sum = 0;
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 3; j++)
{
scanf("%d", &num[i][j]);
temp[num[i][j]] = 1;
if (num[i][j] == 0)
{
row = i; col = j;
}
}
}
for (int i = 1; i <= 9; i++)
{
if (temp[i] != 1)
num[row][col] = i;
}
for (int i = 0; i < 3; i++)
{
scanf("%d %d", &row, &col);
printf("%d\n", num[row - 1][col - 1]);
}
int n;
scanf("%d", &n);
switch (n)
{
case 1:
sum = num[0][0] + num[0][1] + num[0][2];
break;
case 2:
sum = num[1][0] + num[1][1] + num[1][2];
break;
case 3:
sum = num[2][0] + num[2][1] + num[2][2];
break;
case 4:
sum = num[0][0] + num[1][0] + num[2][0];
break;
case 5:
sum = num[0][1] + num[1][1] + num[2][1];
break;
case 6:
sum = num[0][2] + num[1][2] + num[2][2];
break;
case 7:
sum = num[0][0] + num[1][1] + num[2][2];
break;
case 8:
sum = num[0][2] + num[1][1] + num[2][0];
break;
}
int number[19] = { 10000,36,720,360,80,252,108,72,54,180,72,180,119,36,306,1080,144,1800,3600 };
printf("%d", number[sum - 6]);
return 0;
}注意事项：
被0覆盖的数字需要复原，便于后面计算。
如有疑问，欢迎提出。
L1-073 人与神
跨界大神 L. Peter Deutsch 有一句名言：“To iterate is human, to recurse divine.”（迭代的是人，递归的是神）。本题就请你直接在屏幕上输出这句话。
输入格式：
本题没有输入。
输出格式：
在一行中输出 To iterate is human, to recurse divine.。
#include <stdio.h>
int main()
{
printf("To iterate is human, to recurse divine.");
return 0;
}注意事项：
如有疑问，欢迎提出。
L1-074 两小时学完C语言
知乎上有个宝宝问：“两个小时内如何学完 C 语言？”当然，问的是“学完”并不是“学会”。
假设一本 C 语言教科书有 N 个字，这个宝宝每分钟能看 K 个字，看了 M 分钟。还剩多少字没有看？
输入格式：
输入在一行中给出 3 个正整数，分别是 N（不超过 400 000），教科书的总字数；K（不超过 3 000），是宝宝每分钟能看的字数；M（不超过 120），是宝宝看书的分钟数。
题目保证宝宝看完的字数不超过 N。
输出格式：
在一行中输出宝宝还没有看的字数。
输入样例：
100000 1000 72
输出样例：
28000
#include <stdio.h>
int main()
{
int a,b,c;
scanf("%d %d %d",&a,&b,&c);
printf("%d",a-b*c);
return 0;
}注意事项：
如有疑问，欢迎提出。
L1-075 强迫症
小强在统计一个小区里居民的出生年月，但是发现大家填写的生日格式不统一，例如有的人写 199808，有的人只写 9808。有强迫症的小强请你写个程序，把所有人的出生年月都整理成 年年年年-月月 格式。对于那些只写了年份后两位的信息，我们默认小于 22 都是 20 开头的，其他都是 19 开头的。
输入格式：
输入在一行中给出一个出生年月，为一个 6 位或者 4 位数，题目保证是 1000 年 1 月到 2021 年 12 月之间的合法年月。
输出格式：
在一行中按标准格式 年年年年-月月 将输入的信息整理输出。
输入样例1：
9808
输出样例1：
1998-08
输入样例2：
0510
输出样例2：
2005-10
输入样例3：
196711
输出样例3：
1967-11
#include <stdio.h>
#include <string.h>
int main()
{
int num;
scanf("%d", &num);
if (num >= 100000)
printf("%d-%02d", num / 100, num % 100);
else {
int yy;
if (num / 100 < 22)
yy = 20;
else
yy = 19;
printf("%d%02d-%02d", yy, num / 100, num % 100);
}
return 0;
}注意事项：
如有疑问，欢迎提出。
扫一扫
832
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
