LeetCode938. 二叉搜索树的范围和的三种解法:中序+递归+深搜100%+97%（超高效的解法！！！！）

https://leetcode-cn.com/problems/range-sum-of-bst/

题意

给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

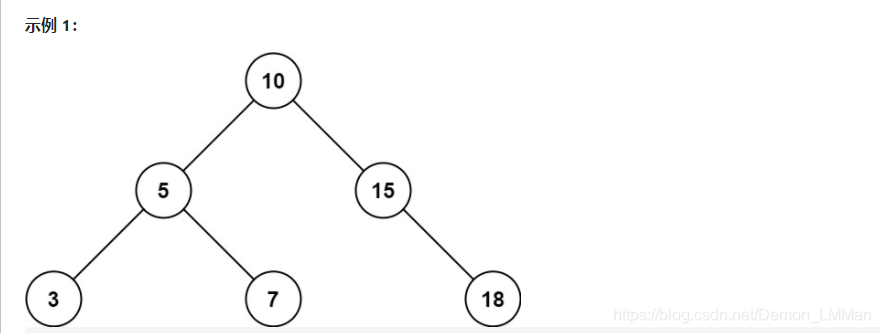
输入：root = [10,5,15,3,7,null,18], low = 7, high = 15
输出：32

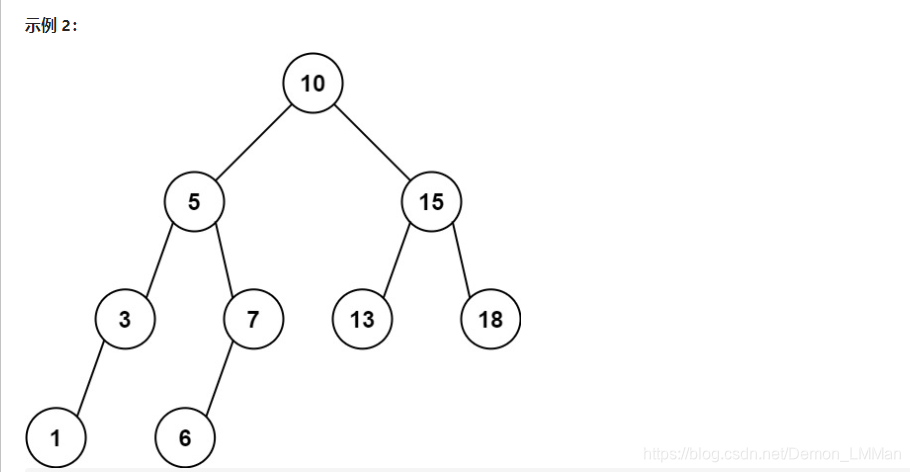
输入：root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
输出：23

题解

1.中序遍历

由于题目中要求求出二叉搜索树中满足范围的所有节点值之和，可以采用中序遍历的方式访问二叉搜索树，这样，访问节点的值就是从小到大递增的。再设置一个布尔变量stop记录访问状态，如果当前访问到的节点值已经大于最大边界high，则停止遍历。

//中序遍历解法
class Solution {
    int sum=0;
    boolean stop=false;
    public int rangeSumBST(TreeNode root, int low, int high) {
        if(root==null||stop)return 0;
        rangeSumBST(root.left,low,high);
        if(low<=root.val&&root.val<=high)sum+=root.val;
        if(high<=root.val)stop=true;
        rangeSumBST(root.right,low,high);
        return sum;
    }
}

2.递归

rangeSumBST方法要实现的功能是，求出以root为根节点的二叉搜索树满足low<=val<=high的节点值的和，并返回。则对root的左右节点调用该方法就可以获得左右子树满足此条件的节点值之和，此时再判断当前节点是否满足条件，就可以得到整棵二叉树满足条件的节点和。当然，还要考虑边界条件，当节点为空时，显然满足条件的节点和是0。
此外，由于是二叉搜索树，所以当root.val<low，即当前节点的值小于了最小边界，那么只要获得右子树的值就可；若high<root.val，也就是当前节点的值大于了最大边界值，只需要获得左子树值即可；而剩下的情况，也就是处于low和high之间，此时需要返回左子树+当前节点+右子树的值。

class Solution {
   public int rangeSumBST(TreeNode root, int low, int high) {
       if(root==null)return 0;
       if(root.val<low)
           return rangeSumBST(root.right,low,high);
       else if(high<root.val)
           return rangeSumBST(root.left,low,high);
       else
           return rangeSumBST(root.left,low,high)+root.val+rangeSumBST(root.right,low,high);
   }
}

3.深搜方法

在二叉树中，深搜的遍历顺序与先序遍历是相同的，即先访问头节点，再访问左右子树。只不过在此可以同过对头节点值的判断，来选择是否进入左右子树访问，从本质上讲，和之前的递归方法并没有区别，只不过在此设置了一个变脸sum，将每次符合条件的节点值加到sum中。

/**
* 深搜解法
*/
class Solution {
    int sum=0;
    public int rangeSumBST(TreeNode root, int low, int high) {
        dfs(root,low,high);
        return sum;
    }

    private void dfs(TreeNode root, int low, int high){
        if(root==null)return ;
        //process 处理节点
        if(low<=root.val&&root.val<=high)
            sum+=root.val;
        //drill down 依次进入下一层
        if(low<root.val)
            rangeSumBST(root.left,low,high);
        if(root.val<high)
            rangeSumBST(root.right,low,high);
    }
}