[SDOI2017]数字表格，洛谷P3704，莫比乌斯反演+狄利克雷卷积

最新推荐文章于 2021-01-14 15:37:26 发布

原创最新推荐文章于 2021-01-14 15:37:26 发布 · 388 阅读

1 ·

CC 4.0 BY-SA版权

数论同时被 2 个专栏收录

49 篇文章

订阅专栏

莫比乌斯反演

12 篇文章

订阅专栏

本文介绍了一种算法竞赛中常见的解题技巧，利用狄利克雷卷积和整除分块技术解决复杂数学问题。通过枚举gcd和预处理前缀积，实现O(nlnn)的高效算法。

正题

题目链接

求 $\prod_{i=1}^n\prod_{j=1}^m f[gcd(i,j)]$ 。

换一个计算方法，枚举gcd，答案就是 $\prod_{g=1}^n f[g]^{t[g]}$ 。

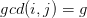其中 t[g] 就是 gcd(i,j)=g 的个数。

那么

$\\t[g]=\sum_{i=1}^n\sum_{j=1}^m[gcd(i,j)=g] \\=\sum_{i=1}^{\frac{n}{g}}\sum_{j=1}^{\frac{m}{g}}[gcd(i,j)=1] \\=\sum_{i=1}^{\frac{n}{g}}\sum_{j=1}^{\frac{m}{g}}\sum_{d\mid gcd(i,j)}\mu(d) \\=\sum_{d=1}^{\frac{n}{g}}\mu(d)\frac{n}{dg}\frac{m}{dg} \\=\sum_{T=1}^n\frac{n}{T}\frac{m}{T}\sum_{dg=T} \mu(d)$

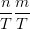换进去，答案就是 $\prod_{g=1}^nf[g]^{\sum_{T=1}^n\frac{n}{T}\frac{m}{T}\sum_{dg=T}\mu(d)}$

枚举T，就变成 $\prod_{T=1}^n \prod_{g\mid T} (f[g]^{\mu(\frac{T}{g})})^{\frac{n}{T}\frac{m}{T}}$

显然可以把 $\frac{n}{T}\frac{m}{T}$ 提出来。

就变成 $\prod_{T=1}(\prod_{g\mid T}f[g]^{\mu(\frac{T}{g})})^{\frac{n}{T}\frac{m}{T}}$

括号里面的设为F， $F[T]=\prod_{g\mid T}f[g]^{\mu(\frac{T}{g})}$ 。

很明显是一个另类的狄利克雷卷积的形式。

做一遍O(n ln n)，然后整除分块，算一下F的前缀积就可以了。

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
using namespace std;

int T,n,m;
const int maxn=1e6;
long long f[maxn+10],mod=1e9+7,g[maxn+10],tot[maxn+10],inv[maxn+10];
int mu[maxn+10],p[maxn+10],temp;
bool vis[maxn+10];

long long ksm(long long x,long long t){
    long long tot=1;
    while(t){
        if(t&1) (tot*=x)%=mod;
        (x*=x)%=mod;
        t/=2;
    }
    return tot;
}

int main(){
    scanf("%d",&T);
    f[0]=0;inv[1]=f[1]=1;mu[1]=1;vis[1]=true;
    for(int i=2;i<=maxn;i++) f[i]=(f[i-2]+f[i-1])%mod,inv[i]=ksm(f[i],mod-2);
    for(int i=2;i<=maxn;i++){
        if(!vis[i]) {mu[i]=-1;p[++p[0]]=i;}
        for(int j=1;j<=p[0] && (temp=i*p[j])<=maxn;j++){
            vis[temp]=true;
            if(i%p[j]==0) break;
            mu[temp]=-mu[i];
        }
    }
    for(int i=1;i<=maxn;i++) g[i]=1;
    tot[0]=1;
    for(int i=1;i<=maxn;i++){
    	if(mu[i]!=0)
	        for(int j=i;j<=maxn;j+=i)
	            (g[j]*=(mu[i]==1?f[j/i]:inv[j/i]))%=mod;
        tot[i]=tot[i-1]*g[i]%mod;
    }
    int l,r;
    long long ans=0;
    while(T--){
        scanf("%d %d",&n,&m);
        ans=1;l=1;
        if(m<n) swap(n,m);
        while(l<=n){
            r=min(n/(n/l),m/(m/l));
            (ans*=ksm(tot[r]*ksm(tot[l-1],mod-2)%mod,(long long)(n/l)*(m/l)%(mod-1)))%=mod;
            l=r+1;
        }
        printf("%lld\n",ans);
    }
}