leetcode刷题详解四

最新推荐文章于 2025-11-24 16:32:05 发布

原创最新推荐文章于 2025-11-24 16:32:05 发布 · 104 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #linux #算法

文章讲述了如何使用递归和双指针技巧解决LeetCode中的链表问题，包括翻转每组k个节点和二叉树的翻转、路径和计算等，强调了递归原理和处理细节的重要性。

25. K 个一组翻转链表

这道题本质上还是用的反转前n个链表的思想。

具体细节如下：

先调用一次函数，使用一个newHead接受返回值，这个是为了方便最后函数的返回。

调用reverseN这个函数的时候，要标记反转这段链表的前置节点和后置节点。后面会用到。

反转后的这部分区间的链表，node接受前置节点，tail接受后置接点。

记住，前一个区间的tail节点就是区间中的最后一个节点，这个节点要放到tail_temp中，然后调用reverseN后，会得到新的tail节点，让tail_temp->next指向tail节点，这样两个区间就会接上。

	ListNode* dummy = nullptr;
    ListNode* tail = nullptr;
    
    ListNode* reverseKGroup(ListNode* head, int k) {
        int length = 0;
        ListNode* temp = head;
        
        if(k == 1){
            return head;
        }
        /*计算链表长度*/
        while(temp){
            temp = temp->next;
            length++;
        }
        //减一是因为第一次的时候，要确定head指针
        int loop = length / k - 1;
        ListNode* newHead = reverseN(k, head);
        head = dummy;
        for(int i = 0;i < loop;i++){
            head = dummy;
            ListNode* tail_temp = tail;
            ListNode* node = reverseN(k, head);
            tail_temp->next = node;
        }
        return newHead;
    }

    ListNode* reverseN(int n, ListNode* head){
        if(n == 1){
            dummy = head->next;
            return head;
        }
        ListNode* last = reverseN(n-1, head->next);
        head->next->next = head;
        head->next = dummy;
        tail = head;
        return last;
    }

剑指 Offer 06. 从尾到头打印链表

递归的做法

其实做了这么多次回头再来看这道题发现一个问题，即链表的本质是改变连接方向就行，而在改变连接方向的时候一定要断开之前的链子，即node->next=null

vector<int> reversePrint(ListNode* head) {
    vector<int> res;
    ListNode* newHead =  reverse(head);
    while(newHead){
        res.push_back(newHead->val);
        newHead = newHead->next;
    }
    return res;
}

ListNode* reverse(ListNode* head){
    if(!head || !head->next){
        return head;
    }
    ListNode* tmp = reverse(head->next);
    head->next->next = head;
    head->next = nullptr;
    return tmp;
}

双指针递归的做法

这也不失为一种思路
用一个辅助栈就行
c++的reverse函数，放到数组里面直接反转

剑指 Offer 24. 反转链表

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
       if(!head || !head->next){
           return head;
       } 
       ListNode* tmp = reverseList(head->next);
       head->next->next = head;
       head->next = nullptr;
       return tmp;
    }
};

剑指 Offer 35. 复杂链表的复制

暴力复制法

先复制俩表的next节点，然后依次寻找每个节点的random指针，时间复杂度 $O(n^2)$
辅助空间

整个hash表，记录一下random指针的位置，然后复制的时候填进去就行，空间复杂度 $O (n)$

终极牛逼法

时间复杂度 $O (n)$

第三步就是拆分

**关键点，不能改原链表，你加完重复链表之后需要复原，！！！**不然会报Next pointer of node with label 7 from the original list was modified.这种错误，表示修改了原链表

class Solution {
public:
    Node* copyRandomList(Node* head) {
        if(!head){
            return head;
        }
        Node* new_head = nullptr; 
        new_head = head;
        //重复每个链表节点
        while(new_head){
            Node* tmp = new Node(new_head->val);
            tmp->next = new_head->next;
            new_head->next = tmp;
            new_head = new_head->next->next;
        }
        new_head = head;
        //重定义random指针
        while(new_head){
            if(new_head->random != nullptr){
                new_head->next->random = new_head->random->next;
            }
            new_head = new_head->next->next;
        }

        //把处于偶数的链表拿出来
        Node* copy_head = head->next;
        Node* copy_head_return = head->next;
        new_head = head;
        while(copy_head->next){
            new_head->next = new_head->next->next;
            new_head = new_head->next;
            copy_head->next = new_head->next;
            copy_head = copy_head->next;
        }
        new_head->next = nullptr;
        return copy_head_return;
    }
};

++++

树相关

树题目的总结

个人对递归的一些感悟。

递归的原理非常简单，就是函数出栈入栈。

但很多时候我们都会被递归绕晕，原因就是我们想的太复杂了。做题的时候，一定要先明确函数的定义是什么，然后根据定义来写递归语句。记住，千万不要跳入递归的细节，有时候不考虑细节反而容易实现，考虑细节的话可能会绕进去！

写树相关的算法，简单说就是，先搞清楚当前 root 节点「该做什么」以及「什么时候做」，然后根据函数定义递归调用子节点

把递归的问题放眼到三个节点中，即根节点，右节点左节点。

重中之重！！！！！！！

递归函数什么时候有返回值什么时候没有返回值，比如有 root->left = invertTree(root->left);这种和return searchBST(root->left,val);这两种代码到底有何区别的？

答：有以下三点:

如果需要搜索整棵二叉树且不用处理递归返回值，递归函数就不要返回值。（这种情况就是本文下半部分介绍的113.路径总和ii）
如果需要搜索整棵二叉树且需要处理递归返回值，递归函数就需要返回值。（这种情况我们在236. 二叉树的最近公共祖先 (opens new window)中介绍）
如果要搜索其中一条符合条件的路径，那么递归一定需要返回值，因为遇到符合条件的路径了就要及时返回。（本题的情况）

普通二叉树相关

226. 翻转二叉树

只要把二叉树上的每一个节点的左右子节点进行交换，最后的结果就是完全翻转之后的二叉树。

只能用后序和前序，不能用中序。因为需要交换左右子节点，必须先知道左右子节点。如果用中序的话只知道左节点和根节点，不知道右节点，无法反转。

注意节点交换细节，和普通变量一样

TreeNode* invertTree(TreeNode* root) {
        if(!root){
            return NULL;
        }
        TreeNode* temp = root->left;
        root->left = root->right;
        root->right = temp;

        root->left = invertTree(root->left);
        root->right = invertTree(root->right);
        return root;
    }

112. 路径总和

二叉树路径问题解析

bool hasPathSum(TreeNode* root, int sum) {
    if(!root){
        return false;
    }
    sum -= root->val;
    if(!root->left && !root->right){
        return sum == 0;
    }
    return hasPathSum(root->left, sum) || hasPathSum(root->right, sum);

}

113. 路径总和 II

vector<vector<int>> res;
    vector<int> tmp;
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        recurse(root, targetSum);
        return res;
    }

    void recurse(TreeNode* root, int targetSum){
        if(!root){
            return;
        }
        tmp.push_back(root->val);
        targetSum -= root->val;
        if(!root->left && !root->right && targetSum == 0){
            res.emplace_back(tmp);
        }
        recurse(root->left, targetSum);
        recurse(root->right, targetSum);
        tmp.pop_back();
    }

116. 填充每个节点的下一个右侧节点指针

还是老样子，关注局部的三个节点，根左右，然后写出代码。

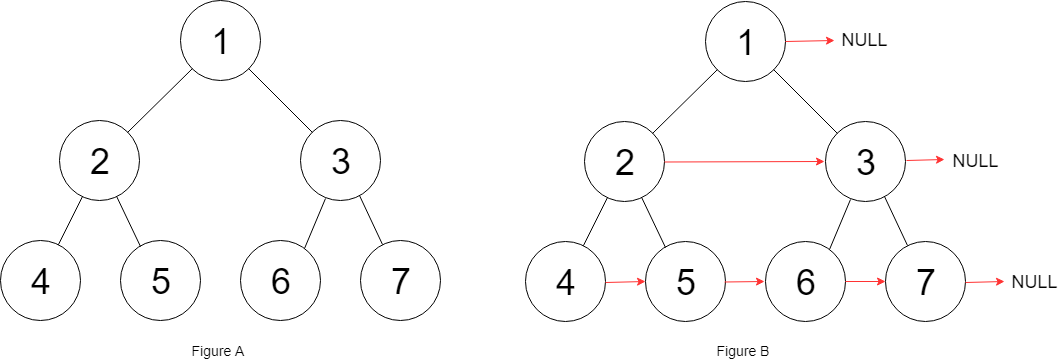
关键点不是2->3这种一个根节点下的节点，而是5->6这种不在同一个根节点下的。因此要借助5和6的上层节点2,3来解决问题。通过2到3，再到6，就可以链接5和6

Node* connect(Node* root) {
        if(!root){
            return NULL;
        }
        if(root->left){
            root->left->next = root->right;
            if(root->next && root->right){
                root->right->next = root->next->left;
            }
        }
        connect(root->left);
        connect(root->right);
        return root;
    }