【MSCKF】LLT-SRF

最新推荐文章于 2025-12-01 19:45:15 发布

原创最新推荐文章于 2025-12-01 19:45:15 发布 · 818 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #xr #vr #mr #visual studio

MSCKF 专栏收录该内容

11 篇文章

订阅专栏

LLT-based SRF与EKF等效性的完整推导过程（从EKF后验协方差公式出发）

一、推导前置准备

在正式推导前，需明确核心符号定义和关键矩阵性质，确保推导逻辑连贯：
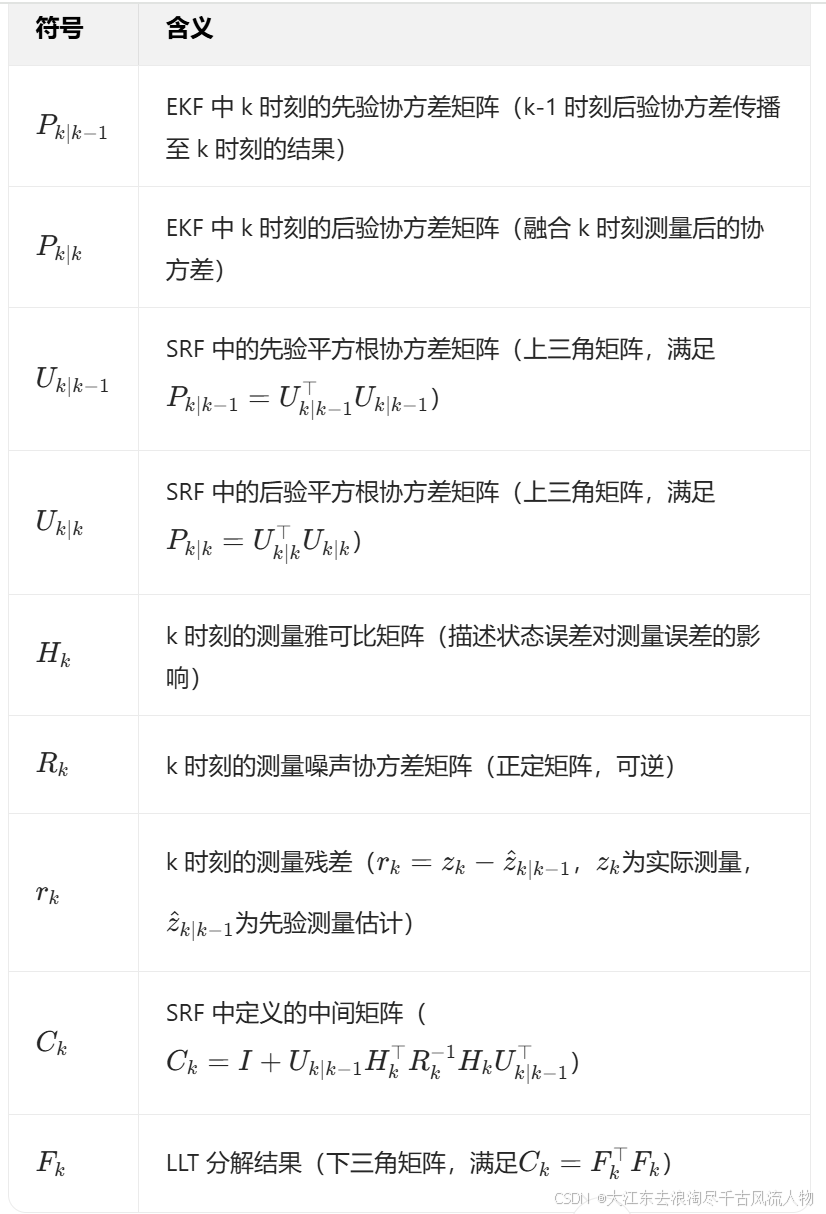
在这里插入图片描述

关键矩阵性质：

上三角矩阵的转置是下三角矩阵，下三角矩阵的逆仍是下三角矩阵；
矩阵逆的性质：( $AB)^{-1} = B^{-1} A^{-1}$ )（A、B均可逆）；
Woodbury恒等式（核心恒等变换工具）：对可逆矩阵( A )、( B )及任意矩阵( C )，满足
( $C^\top)^{-1} = A^{-1} - A^{-1} C (B^{-1} + C^\top A^{-1} C)^{-1} C^\top A^{-1}$ )；
正定矩阵的Cholesky分解唯一：若( M )是正定矩阵，则存在唯一下三角矩阵( L )，使得( $L^\top$ )（本文中记为LLT分解）。

二、第一部分：后验协方差更新等效性（证明( $Pk∣k=Uk∣k⊤Uk∣kP_{k|k} = U_{k|k}^\top U_{k|k}$ )

步骤1：写出EKF的后验协方差公式（推导起点）

EKF的核心是通过“先验协方差+测量修正”得到后验协方差，其标准公式为：
$P_{k|k} = P_{k|k-1} - P_{k|k-1} H_k^\top \underbrace{(H_k P_{k|k-1} H_k^\top + R_k)^{-1}}_{卡尔曼增益中的逆项} H_k P_{k|k-1} \tag{1}$
公式含义：

右侧第一项( $P_{k|k-1}$ )是“未融合测量的先验协方差”；
第二项是“测量带来的协方差修正项”（通过卡尔曼增益的核心逆项调整，体现测量对状态不确定性的压缩）。

步骤2：代入SRF的核心定义( $Pk∣k−1=Uk∣k−1⊤Uk∣k−1P_{k|k-1} = U_{k|k-1}^\top U_{k|k-1}$ )

SRF的本质是用“平方根协方差矩阵( U )”替代“传统协方差矩阵( P )”，因此将公式(1)中所有( $P_{k|k-1}$ )替换为( $Uk∣k−1⊤Uk∣k−1U_{k|k-1}^\top U_{k|k-1}$ )（利用( $U^\top U$ )）：
$P_{k|k} = U_{k|k-1}^\top U_{k|k-1} - U_{k|k-1}^\top U_{k|k-1} H_k^\top (H_k U_{k|k-1}^\top U_{k|k-1} H_k^\top + R_k)^{-1} H_k U_{k|k-1}^\top U_{k|k-1} \tag{2}$
替换依据：矩阵乘法满足结合律，即( $Pk∣k−1Hk⊤=(Uk∣k−1⊤Uk∣k−1)Hk⊤=Uk∣k−1⊤(Uk∣k−1Hk⊤)P_{k|k-1} H_k^\top = (U_{k|k-1}^\top U_{k|k-1}) H_k^\top = U_{k|k-1}^\top (U_{k|k-1} H_k^\top)$ )。

将( $Uk∣k−1⊤U_{k|k-1}^\top$ )和( $U_{k|k-1}$ )分别提取到括号外（利用矩阵乘法分配律），公式(2)可整理为：
$P_{k|k} = U_{k|k-1}^\top \left[ I - U_{k|k-1} H_k^\top (H_k U_{k|k-1}^\top U_{k|k-1} H_k^\top + R_k)^{-1} H_k U_{k|k-1}^\top \right] U_{k|k-1} \tag{3}$
整理目的：凸显括号内的“单位矩阵修正项”，为后续利用Woodbury恒等式化简做准备。

步骤3：用Woodbury恒等式化简括号内的核心项

公式(3)中括号内的项是推导的关键，记为( $U_{k|k-1} H_k^\top (H_k U_{k|k-1}^\top U_{k|k-1} H_k^\top + R_k)^{-1} H_k U_{k|k-1}^\top$ )，需通过Woodbury恒等式化简。

步骤3.1：定义中间变量简化表达式

令：

( $U_{k|k-1} H_k^\top$ )（因( $U_{k|k-1}$ )是上三角、( $Hk⊤H_k^\top$ )是任意矩阵，( A )为普通矩阵）；
( B = R_k )（测量噪声协方差，正定可逆）。

则( $HkUk∣k−1⊤Uk∣k−1Hk⊤=A⊤AH_k U_{k|k-1}^\top U_{k|k-1} H_k^\top = A^\top A$ )，括号内的项可改写为：
$(A^\top A + B)^{-1} A^\top \tag{4}$

步骤3.2：应用Woodbury恒等式化简( $(A⊤A+B)−1(A^\top A + B)^{-1}$ )

对 $(A⊤A+B)−1(A^\top A + B)^{-1}$ 应用Woodbury恒等式（令Woodbury恒等式中的 $\to A^\top$ 、 $\to B$ 、 $\to I$ ：
$(A^\top A + B)^{-1} = B^{-1} - B^{-1} A^\top (I + A B^{-1} A^\top)^{-1} A B^{-1} \tag{5}$

步骤3.3：将(5)代入(4)，化简得到 $B^{-1} A^\top)^{-1}$

将(5)代入(4)：
$\begin{align*} M &= I - A \left[ B^{-1} - B^{-1} A^\top (I + A B^{-1} A^\top)^{-1} A B^{-1} \right] A^\top \\ &= I - A B^{-1} A^\top + A B^{-1} A^\top (I + A B^{-1} A^\top)^{-1} A B^{-1} A^\top \tag{6} \end{align*}$

令 $B^{-1} A^\top$ （即论文中定义的 $C_k$ ），则 $B^{-1} A^\top = C - I$ ，代入(6)：
$\begin{align*} M &= I - (C - I) + (C - I) C^{-1} (C - I) \\ &= I - C + I + (C - I)(I - C^{-1}) \\ &= 2I - C + (C \cdot I - C \cdot C^{-1} - I \cdot I + I \cdot C^{-1}) \\ &= 2I - C + (C - I - I + C^{-1}) \\ &= C^{-1} \end{align*}$

最终得到关键化简结果：
$B^{-1} A^\top)^{-1} = \underbrace{(I + U_{k|k-1} H_k^\top R_k^{-1} H_k U_{k|k-1}^\top)}_{C_k} ^{-1} \tag{7}$

步骤4：引入LLT分解，定义SRF的后验平方根协方差( U_{k|k} )

步骤4.1：对( C_k )进行LLT分解

由论文定义，( $Ck=I+Uk∣k−1Hk⊤Rk−1HkUk∣k−1⊤C_k = I + U_{k|k-1} H_k^\top R_k^{-1} H_k U_{k|k-1}^\top$ )：

因( R_k )正定，( $R_k^{-1}$ )正定；
( $Uk∣k−1Hk⊤Rk−1HkUk∣k−1⊤U_{k|k-1} H_k^\top R_k^{-1} H_k U_{k|k-1}^\top$ )是“矩阵二次型”，为半正定矩阵；
半正定矩阵加单位矩阵（正定）后，( C_k )是严格正定矩阵，满足Cholesky分解条件。

对( C_k )进行LLT分解（下三角Cholesky分解），得到唯一的下三角矩阵( F_k )，满足：
$C_k = F_k^\top F_k \tag{8}$

步骤4.2：推导( U_{k|k} )的表达式

将(7)和(8)代入公式(3)，EKF的后验协方差可改写为：
$P_{k|k} = U_{k|k-1}^\top C_k^{-1} U_{k|k-1} = U_{k|k-1}^\top (F_k^\top F_k)^{-1} U_{k|k-1} \tag{9}$

利用矩阵逆的性质( $(Fk⊤Fk)−1=Fk−1Fk−⊤(F_k^\top F_k)^{-1} = F_k^{-1} F_k^{-\top}$ )（( $F_k$ )是下三角矩阵，( $F_k^{-1}$ )仍是下三角，( $Fk−⊤F_k^{-\top}$ )是上三角），代入(9)：
$P_{k|k} = U_{k|k-1}^\top F_k^{-1} F_k^{-\top} U_{k|k-1} \tag{10}$

根据SRF的核心定义（( $Pk∣k=Uk∣k⊤Uk∣kP_{k|k} = U_{k|k}^\top U_{k|k}$ )），对比(10)两侧的矩阵结构：

左侧( $Pk∣k=Uk∣k⊤Uk∣kP_{k|k} = U_{k|k}^\top U_{k|k}$ )（( $U_{k|k}$ )是上三角矩阵）；
右侧( $Uk∣k−1⊤Fk−1Fk−⊤Uk∣k−1=(Fk−⊤Uk∣k−1)⊤(Fk−⊤Uk∣k−1)U_{k|k-1}^\top F_k^{-1} F_k^{-\top} U_{k|k-1} = (F_k^{-\top} U_{k|k-1})^\top (F_k^{-\top} U_{k|k-1})$ )（因( $(AB)⊤=B⊤A⊤(AB)^\top = B^\top A^\top$ )，且( $Fk−⊤F_k^{-\top}$ )是上三角、( U_{k|k-1} )是上三角，两者乘积仍是上三角）。

因此，可定义SRF的后验平方根协方差矩阵：
$U_{k|k} = F_k^{-\top} U_{k|k-1} \tag{11}$

将(11)代入(10)，最终得到：
$P_{k|k} = U_{k|k}^\top U_{k|k} \tag{12}$

结论1：EKF的后验协方差( P_{k|k} )与LLT-based SRF的后验协方差（$( U_{k|k}^\top U_{k|k}$ )）完全等效。

三、第二部分：状态更新量等效性（证明( $Kkrk=Uk∣k⊤Uk∣kHk⊤Rk−1rkK_k r_k = U_{k|k}^\top U_{k|k} H_k^\top R_k^{-1} r_k$ )）

EKF的状态更新公式为( $x^k∣k=x^k∣k−1+Kkrk\hat{x}_{k|k} = \hat{x}_{k|k-1} + K_k r_k$ )，其中( $Kk=Pk∣k−1Hk⊤(HkPk∣k−1Hk⊤+Rk)−1K_k = P_{k|k-1} H_k^\top (H_k P_{k|k-1} H_k^\top + R_k)^{-1}$ )是卡尔曼增益。需证明( $Kkrk=Uk∣k⊤Uk∣kHk⊤Rk−1rkK_k r_k = U_{k|k}^\top U_{k|k} H_k^\top R_k^{-1} r_k$ )。

步骤1：写出EKF的卡尔曼增益与状态更新项

EKF的状态更新修正项为：
$K_k r_k = P_{k|k-1} H_k^\top (H_k P_{k|k-1} H_k^\top + R_k)^{-1} r_k \tag{13}$

步骤2：技巧性拆分( $r_k = R_k R_k^{-1} r_k$ )

为关联第一部分的协方差结果，将( r_k )拆分为“( $Rk×Rk−1rkR_k \times R_k^{-1} r_k$ )”（因( R_k )可逆，拆分不改变原表达式）：
$K_k r_k = P_{k|k-1} H_k^\top (H_k P_{k|k-1} H_k^\top + R_k)^{-1} R_k R_k^{-1} r_k \tag{14}$

步骤3：化简( $(HkPk∣k−1Hk⊤+Rk)−1Rk(H_k P_{k|k-1} H_k^\top + R_k)^{-1} R_k$ )

利用矩阵逆的恒等式：对任意可逆矩阵( X )、( Y )，满足( $X + Y)^{-1} Y = I - (X + Y)^{-1} X$ )。令( $H_k P_{k|k-1} H_k^\top$ )、( $Y = R_k$ )，则：
$(H_k P_{k|k-1} H_k^\top + R_k)^{-1} R_k = I - (H_k P_{k|k-1} H_k^\top + R_k)^{-1} H_k P_{k|k-1} H_k^\top \tag{15}$

将(15)代入(14)：
$Kkrk=Pk∣k−1Hk⊤[I−(HkPk∣k−1Hk⊤+Rk)−1HkPk∣k−1Hk⊤]Rk−1rk=[Pk∣k−1Hk⊤−Pk∣k−1Hk⊤(HkPk∣k−1Hk⊤+Rk)−1HkPk∣k−1Hk⊤]Rk−1rk\begin{align*} K_k r_k &= P_{k|k-1} H_k^\top \left[ I - (H_k P_{k|k-1} H_k^\top + R_k)^{-1} H_k P_{k|k-1} H_k^\top \right] R_k^{-1} r_k \\ &= \left[ P_{k|k-1} H_k^\top - P_{k|k-1} H_k^\top (H_k P_{k|k-1} H_k^\top + R_k)^{-1} H_k P_{k|k-1} H_k^\top \right] R_k^{-1} r_k \tag{16} \end{align*}$

步骤4：提取公因子( $Hk⊤H_k^\top$ )，关联后验协方差( $P_{k|k}$ )

观察(16)括号内的项，两项均包含( H_k^\top )，利用矩阵乘法结合律提取公因子( H_k^\top )到括号外：
$K_k r_k = \underbrace{\left[ P_{k|k-1} - P_{k|k-1} H_k^\top (H_k P_{k|k-1} H_k^\top + R_k)^{-1} H_k P_{k|k-1} \right]}_{P_{k|k} \text{（EKF后验协方差，第一部分公式(1)）}} H_k^\top R_k^{-1} r_k \tag{17}$

步骤5：代入( $Pk∣k=Uk∣k⊤Uk∣kP_{k|k} = U_{k|k}^\top U_{k|k}$ )（第一部分结论）

将第一部分得到的( $Pk∣k=Uk∣k⊤Uk∣kP_{k|k} = U_{k|k}^\top U_{k|k}$ )代入(17)：
[ $K_k r_k = U_{k|k}^\top U_{k|k} H_k^\top R_k^{-1} r_k \tag{18}$ ]

结论2：EKF的状态更新修正项( $K_k r_k$ )与LLT-based SRF的状态更新修正项（( $Uk∣k⊤Uk∣kHk⊤Rk−1rkU_{k|k}^\top U_{k|k} H_k^\top R_k^{-1} r_k$ )）完全等效。

四、完整等效性证明总结

通过上述两部分推导，可得出最终结论：
LLT-based SRF的更新规则与经典EKF完全等效——即：

后验协方差等效：( $Pk∣k=Uk∣k⊤Uk∣kP_{k|k} = U_{k|k}^\top U_{k|k}$ )（由公式(12)证明）；
状态更新等效：( $Kkrk=Uk∣k⊤Uk∣kHk⊤Rk−1rkK_k r_k = U_{k|k}^\top U_{k|k} H_k^\top R_k^{-1} r_k$ )（由公式(18)证明）。

该等效性证明的核心价值在于：

正确性保障：LLT-SRF继承了EKF的数学严谨性，不会因引入“平方根协方差”和“LLT分解”产生额外误差；
优势凸显：相比EKF，LLT-SRF通过“上三角矩阵( U )”和“LLT分解”，避免了( P )矩阵非正定的数值风险，同时减少了存储量（( U )是上三角，存储量为( P )的1/2）和计算量（LLT分解计算量为( O(n^3/3) )，远低于矩阵求逆的( O(n^3) )），完美适配VINS的嵌入式实时需求。