SLAM十四讲笔记1

ch02 初识SLAM

ch02-01 经典视觉SLAM框架

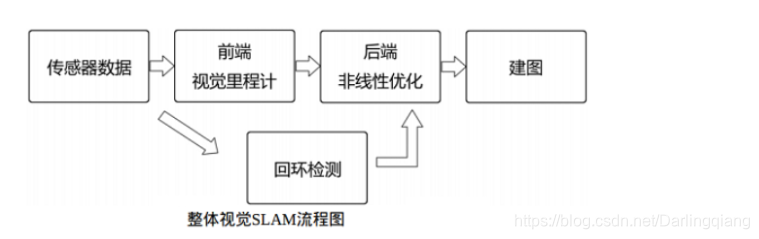
视觉SLAM流程包括以下步骤:

1. 传感器信息读取: 在视觉SLAM中主要为相机图像信息的读取和预处理.如果是在机器人中,还可能有码盘、惯性传感器等信息的读取和同步.
2. 视觉里程计(Visual Odometry,VO): 视觉里程计的任务是估算相邻图像间相机的运动,以及局部地图的样子.VO又称为前端(Front End).

视觉里程计不可避免地会出现累积漂移(Accumulating Drift)问题.

1. 后端优化 (Optimization): 后端接受不同时刻视觉里程计测量的相机位姿,以及回环检测的信息,对它们进行优化,得到全局一致的轨迹和地图.由于接在VO之后,又称为后端(Back End).

在视觉 SLAM中,前端和计算机视觉研究领域更为相关,比如图像的特征提取与匹配等,后端则主要是滤波与非线性优化算法.

1. 回环检测 (Loop Closing): 回环检测判断机器人是否到达过先前的位置.如果检测到回环,它会把信息提供给后端进行处理.
2. 建图 (Mapping): 它根据估计的轨迹,建立与任务要求对应的地图.

地图的形式包括度量地图(精确表示地图物体的位置关系)与拓扑地图(更强调地图元素之间的关系)两种.

ch02-02 SLAM问题的数学表述

“小萝卜携带着传感器在环境中运动”,由如下两件事情描述:

• 1.什么是运动 ?我们要考虑从k − 1时刻到 k 时刻,小萝卜的位置 x 是如何变化的.

运动方程:

​ $$x_k=f(x_{k-1},u_k,w_k)$$

x_k, x_{k-1}$表示小罗卜在k和k-1时刻的位置，$u_k 表示运动传感器的读数(有时也叫输入) ,$w_k$ 表示运动噪声

• 2.什么是观测 ?假设小萝卜在$k$时刻于 x_k处探测到了某一个路标y_j,我们要考虑这件事情是如何用数学语言来描述的.

观测方程:
$$z_{k,j}=h(y_j,x_k,v_{k,j})$$
​
$z_{k,j}$表示小萝卜在$x_k$位置上看到路标点 $x_k$,产生的观测数据; $y_j$表示第 j个路标点 ;$v_{k,j})$表示观测噪声

这两个方程描述了最基本的SLAM问题:当知道运动测量的读数u ,以及传感器的读数z 时,如何求解定位问题(估计x )和建图问题(估计 y).这时,我们就把SLAM问题建模成了一个状态估计问题:如何通过带有噪声的测量数据,估计内部的、隐藏着的状态变量?

ch03 三维空间刚体运动

ch03.01 旋转矩阵：点和向量,坐标系

01 向量a在线性空间的基$[e_1,e_2,e_3]$下的坐标为$[a_1,a_2,a_3{]}^T$.

$$\begin{gathered} a=[e_1,e_2,e_3]\left[a_1 \\ {a}_2 \\ {a}_3\right]=a_1{e}_1+a_2{e}_2+a_3{e}_3 \end{gathered}$$

02 向量的内积与外积

2.1 向量的内积: 描述向量间的投影关系
$$a\cdot b=a^{T}b={\Sigma }_{i-1}^3{a}_1{b}_i=|a||b|cos<a,b>$$

2.2 向量的外积: 描述向量的旋转

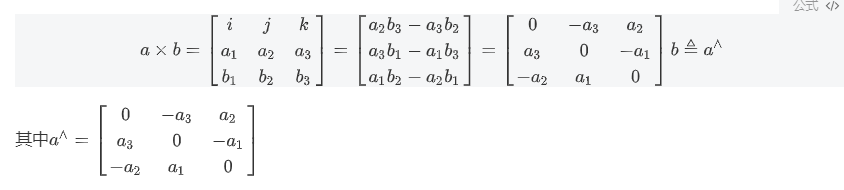
ch03.02 坐标系间的欧氏变换

01:欧式变换:

在欧式变换前后的两个坐标系下,同一个向量的模长和方向不发生改变,是为欧式变换. 一个欧式变换由一个旋转和一个平移组成.

02:旋转矩阵$R$ 的推导 :

设单位正交基$[e_1,e_2,e_3]$ 经过一次旋转变成了 $[e_1^{’},e_2^{’},e_3^{’}]$ 对于同一个向量a,在两个坐标系下的坐标分别为$[a_1,a_2,a_3]$和 $[a_1,a_2,a_3{]}^T$. 根据坐标的定义:
$$[e_1,e_2,e_3]\left[\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right]=[e_1^{’},e_2^{’},e_3^{’}]\left[\begin{array}{c}{a}_1^{’}\\ a_2^{’}\\ a_3^{’}\end{array}\right]$$
等式左右两边同时左乘$[e_1^T,e_2^T,e_3^T]$, 得到
$$\left[\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right]=\left[\begin{array}{ccc}{e}_1^T{e}_1^{’}& e_1^T{e}_2^{’}& e_1^T{e}_3^{’}\\ e_2^T{e}_1^{’}& e_2^T{e}_2^{’}& e_2^T{e}_3^{’}\\ e_3^T{e}_1^{’}& e_3^T{e}_2^{’}& e_3^T{e}_3^{’}\end{array}\right]\left[\begin{array}{c}{a}_1^{’}\\ a_2^{’}\\ a_3^{’}\end{array}\right]\triangleq R{a}^{{}^{\prime }}$$

矩阵$ R$描述了旋转,称为旋转矩阵.

03 旋转矩阵$R$ 的性质

旋转矩阵是**行列式为1的正交矩阵,**任何行列式为1的正交矩阵也是一个旋转矩阵.所有旋转矩阵构成特殊正交群$SO$:
S O ( n ) = { R ∈ R n x n ∣ R R T = I , d e t ( R ) = I } SO(n) = \{ R\in \mathbb{R}^{nxn}|RR^{T} = I, det(R) = I \} SO(n)={R∈Rnxn∣RRT=I,det(R)=I}
旋转矩阵是正交矩阵(其转置等于其逆),旋转矩阵的逆$R^{-1}$ (即转置$R^T$ )描述了一个相反的旋转.

04 欧式变换的向量表示:

世界坐标系中的向量a,经过一次旋转(用旋转矩阵$R$描述)和一次平移(用平移向量$t$描述)后,得到了$a^{’}$
$$a^{’}=Ra+t$$

ch03.03 变换矩阵与齐次坐标

01变换矩阵$T$:

在三维向量的末尾添加1,构成的四维向量称为齐次坐标.将旋转和平移写入变换矩阵$T$中,得到:
$$\left[\begin{array}{c}{a}^{’}\\ 1\end{array}\right]=\left[\begin{array}{cc}R& t\\ 0& 1\end{array}\right]\triangleq T\left[\begin{array}{c}a\\ 1\end{array}\right]$$
齐次坐标的意义在于将欧式变换表示为线性关系**.

02变换矩阵 T 的性质:

变换矩阵$T$构成特殊欧式群$SE$
S E ( 3 ) = { T = [ R t 0 1 ] ∈ R 4 x 4 ∣ R ∈ S O ( 3 ) , t ∈ R 3 } SE(3) =\{ T =\left[\begin{matrix} R &t \\0 &1\end{matrix} \right] \in \mathbb{R}^{4x4}|R\in \mathbb SO(3),t\in \mathbb{R}^{3}\} SE(3)={T=[R0​t1​]∈R4x4∣R∈SO(3),t∈R3}

变换矩阵的逆表示一个反向的欧式变换
$$T^{-1}=\left[\begin{array}{cc}{R}^T& -R^{T}t\\ 0& 1\end{array}\right]$$

ch03.04 齐次坐标(Homogeneous Coordinate)的优势

优势1:方便判断是否在直线或平面上

若点 p = { x , y } p=\{ x,y\} p={x,y},在直线$l=(a,b,c)$上,则有:
$$ax+by+c=[a,b,c{]}^T\cdot [x,y,1]=l^T\cdot p^{’}=0$$
若点 p = { x , y , z } p=\{ x,y,z\} p={x,y,z},在平面$A=(a,b,c,d)$上,则有:
$$ax+by+cz+d=[a,b,c,d{]}^T\cdot [x,y,z,1]=A^T\cdot p^{’}=0$$

优势2:方便表示线线交点和点点共线

在齐次坐标下,

可以用两个点$p,q$的齐次坐标叉乘结果表示它们的共线l
可以用两条直线 $l,m$ 的齐次坐标叉乘结果表示它们的交点 x

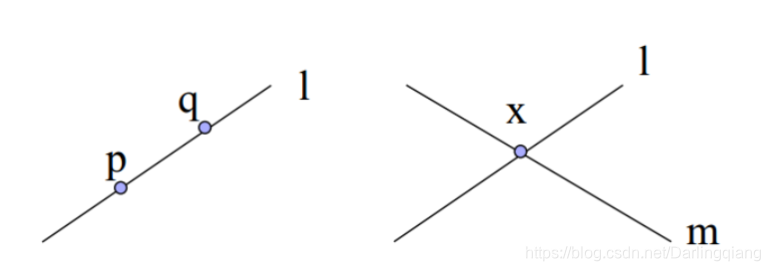
这里利用叉乘的性质: 叉乘结果与两个运算向量都垂直:

性质1的证明:
$$\begin{gathered} l^T\cdot p=(p\times q)\cdot p=0 \\ {l}^T\cdot q=(p\times q)\cdot q=0 \end{gathered}$$
性质2的证明:
$$\begin{gathered} l^T\cdot p=l^T\cdot (l\times m)=0 \\ {m}^T\cdot p=m^T\cdot (l\times m)=0 \end{gathered}$$

优势3:能够区分向量和点

点$(x,y,z)$的齐次坐标为$(x,y,z,1)$
向量$(x,y,z)$的齐次坐标为$(x,y,z,0)$

优势4:能够表达无穷远点

对于平行直线$l=(a,b,c)$和$m=(a,b,d)$,求取其交点的齐次坐标$x=l\times m=(kb,-ka,0)$,将其转为非齐次坐标,得到$x=(kb/0,-ka/0)=(inf,-inf)$,这表示无穷远点.

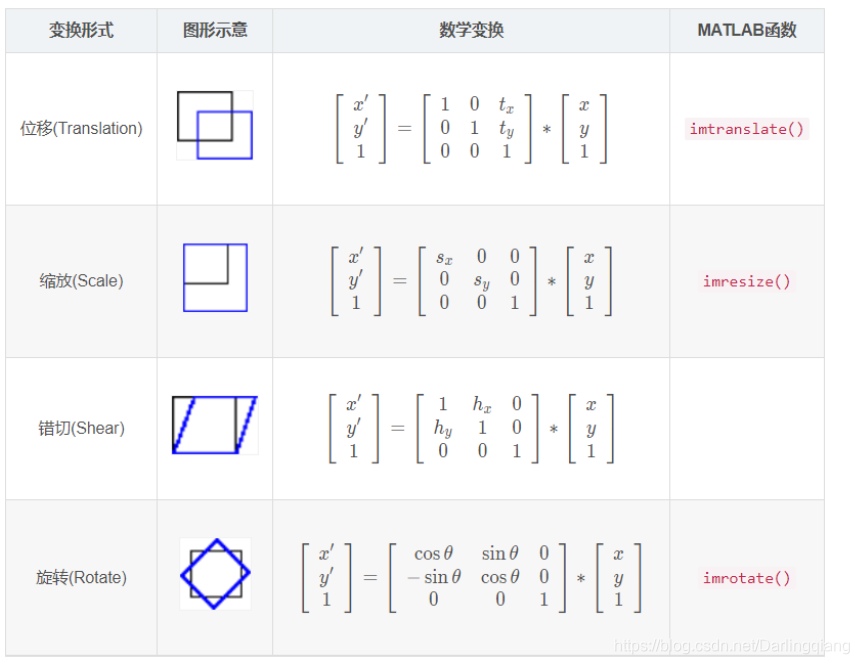
优势5:能够简洁的表示变换

使用齐次坐标,可以将加法运算转化为乘法运算.

ch03.05 旋转向量和欧拉角

01 旋转向量

旋转矩阵的缺点:

1. 旋转矩阵有9个量,但一次旋转只有3个自由度,这种表达方式是冗余的.
2. 旋转矩阵自带约束(必须是行列式为1的正交矩阵),这些约束会给估计和优化带来困难.

旋转向量: 任意旋转都可以用一个旋转轴和一个旋转角 来刻画.于是,我们可以使用一个向量,其方向表示旋转轴而长度表示旋转角.这种向量称为旋转向量(或轴角,Axis-Angle).

假设有一个旋转轴为$ n$,角度为 $\theta$的旋转,其对应的旋转向量为 $\theta n$
旋转向量和旋转矩阵之间的转换:罗德里格斯公式

设旋转向量R表示一个绕单位向量n,角度为θ的旋转.

旋转向量到旋转矩阵:
$$R=cos\theta I+(1-cos\theta )n{n}^T+sin\theta n^{\wedge }$$
旋转矩阵到旋转向量:

旋转角 $\theta =arccos((tr(R)-1)/2)$

旋转轴n是矩阵R RR特征值1对应的特征向量

ch03.06 欧拉角

欧拉角将一次旋转分解成3个分离的转角.常用的一种ZYX转角将任意旋转分解成以下3个轴上的转角:

绕物体的Z轴旋转,得到偏航角yaw
绕旋转之后的Y轴旋转,得到俯仰角pitch
绕旋转之后的X轴旋转,得到滚转角roll

• 欧拉角的一个重大缺点是万向锁问题(奇异性问题): 在俯仰角为$\pm$90° 时,第一次旋转与第三次旋转将使用同一个轴,使得系统丢失了一个自由度(由3次旋转变成了2次旋转).

ch03.07 四元数

为什么需要四元数: 对于三维旋转,找不到不带奇异性的三维向量描述方式.因此引入四元数.四元数是一种扩展的复数,既是紧凑的,也没有奇异性.

01 四元数的定义

1.四元数的定义

一个四元数q qq拥有一个实部和三个虚部
$q=q_0+q_{1}i+q_{2}j+q_{3}k$

其中$i,j,k$,为四元数的3个虚部,它们满足以下关系式(自己和自己的运算像复数,自己和别人的运算像叉乘):
$\begin{array}{r}{i}^2=j^2=k^2=-1\\ ij=k,ji=-k\\ jk=i,kj=-i\\ ki=j,ik=-j\end{array}$

也可以用一个标量和一个向量来表达四元数:
$$q=[s,v],s=q_0\in \mathbb{R},v=[q_1,q_2,q_3{]}^T\in {\mathbb{R}}^{3x3}$$
s为四元数的实部,v 为四元数的虚部.有实四元数和虚四元数的概念.
2.四元数与旋转角度的关系:

在二维情况下,任意一个旋转都可以用单位复数来描述,乘i ii就是绕i ii轴旋转90°.
在三维情况下,任意一个旋转都可以用单位四元数来描述,乘i ii就是绕i ii轴旋转180°.

3.单位四元数和旋转向量之间的转换:

设单位四元数q 表示一个绕单位向量$ n=[n_x,n_y,n_z]^T$,角度为 θ的旋转.

3.1 从旋转向量到单位四元数:
$$q=[cos(\theta /2),nsin(\theta /2){]}^T=[cos(\frac{\theta }{2}),n_{x}sin(\frac{\theta }{2}),n_{y}sin(\frac{\theta }{2}),n_{z}sin(\frac{\theta }{2}){]}^T$$
3.2 从单位四元数到旋转向量
$$\{\begin{array}{rl}\theta & =2arc\cos (q_0)\\ \left[n_x,n_y,n_z\right]& =[q_1,q_2,q_3{]}^T/sin(\frac{\theta }{2})\end{array}$$

02 用单位四元数表示旋转

给定一个空间三维点$p= [ x , y , z ] ∈ R3 ,p=[x,y,z ] R^3, p=[x,y,z]∈R ^3 $,以及一个由轴角n,θ指定的旋转,三维点p 经过旋转后变为p′.如何使用单位四元数q 表达旋转?

1. 把三维空间点用一个虚四元数p 表示:

$$p=[0,x,y,z]=[0,v]$$

2. 把旋转用单位四元数q qq表示:
   $$q=[cos(\frac{\theta }{2}),nsin(\frac{\theta }{2})$$

3. 旋转后的点 p′ 可表示为:
   $$p^{’}=qp{q}^{-1}$$
   这样得到的点p’ 仍为一个纯虚四元数,其虚部的3个分量表示旋转后3D点的坐标.
   只有单位四元数才能表示旋转,因此在程序中创建四元数后,要记得调用normalize()以将其单位化

ch04 李群与李代数

ch04-01 李群与李代数基础

旋转矩阵构成特殊正交群SO(3),变换矩阵构成了特殊欧氏群 SE(3).

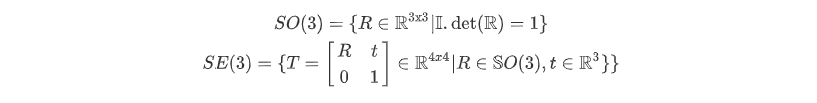
1. 群的定义

群(Group)是一种集合加上一种运算的代数结构.把集合记作A AA,运算记作⋅ \cdot⋅ ,那么群可以记作G = ( A , ⋅ ) G =(A,\cdot)G=(A,⋅).群要求这个运算满足如下条件(封结幺逆):

1. 封闭性 $ ∀a_1,a_2∈A,a_1⋅a_2∈A. $

2. 结合律 $ ∀ a_1,a_2,a_3∈A,(a_1⋅a_2)⋅a_3=a_1⋅(a_2⋅a_3) $

3. 幺元 $ ∃ a_0∈A,s.t.∀ a∈A, a_0⋅a=a⋅a_0=a $

4. 逆：$ ∀ a∈A,∃ a^{−1}∈ A ,s.t.a⋅a^{−1}=a{0}$

   李群是指具有连续(光滑)性质的群SO(3)和SE(3)都是李群

2. 李代数的定义

每个李群都有与之对应的李代数,李代数描述了李群的局部性质.

通用的李代数的定义如下:
李代数由一个集合V,一个数域 F 和一个二元运算[ , ] 组成.如果它们满足以下几条性质,则称$(V,F,[,])$为一个李代数,记作$ g $.

1. 封闭性: $ ∀ X,Y∈V,[X,Y]∈V. $

2. 双线性: $ \forall X,Y,Z \in V, a,b \in F $
   $$[aX+bY,Z]=a[X,Z]+b[Y,Z],[Z,aX+bY]=a[Z,X]+b[Z,Y]$$

3. 自反性: $ ∀X,∈V,[X,X]=0. $

4. 雅可比等价$ ∀ X,Y,Z∈V,[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0 $.其中的二元运算$[ , ]$ [,][,]被称为李括号.例如三维向量空间${\mathbb{R}}^3$ 上定义的叉积× \times×是一种李括号.

3. 李代数so(3)

3.1 李群SO(3)对应的李代数so(3)是定义在$ \mathbb{R^3}$ 上的向量,记作$\varphi$.
s o ( 3 ) = { ϕ ∈ R 3 , Φ = ϕ ∧ = a ∧ = [ 0 − ϕ 3 ϕ 2 ϕ 3 0 − ϕ 1 − ϕ 2 ϕ 1 0 ] ∈ R 3 x 3 } so(3)=\{ \phi \in \mathbb R^{3},\Phi=\phi^∧ = {a}^∧ =\left[\begin{matrix} &0 & -\phi_3 &\phi_2 \\ &\phi_3 &0 &-\phi_1 \\ &-\phi_2 & \phi_1 &0\end{matrix} \right] \in \mathbb R^{3x3} \} so(3)={ϕ∈R3,Φ=ϕ∧=a∧=⎣⎡​​0ϕ3​−ϕ2​​−ϕ3​0ϕ1​​ϕ2​−ϕ1​0​⎦⎤​∈R3x3}

3.2 李代数so(3)的李括号为
$$[{\varphi }_1,{\varphi }_2]=({\Phi }_1{\Phi }_2-{\Phi }_2{\Phi }_1{)}^{\vee }$$
其中 ∨ 是 ^ 的逆运算,表示将反对称矩阵还原为向量
3.3 so(3)和SO(3)间的映射关系为

• 李群$R=exp({\varphi }^{\wedge })=exp(\Phi )$
• 李代数$\varphi =ln(R{)}^{\vee }$

3.4 李代数se(3)

类似地,李群SE(3)的李代数se(3)是定义在 ${\mathbb{R}}^6$上上的向量.记作$\xi$:
s e ( 3 ) = { ξ = [ ρ , ϕ ] ∈ R 6 , ρ ∈ R 3 , ξ ∧ = [ 0 − ϕ 3 ϕ 2 ϕ 3 0 − ϕ 1 − ϕ 2 ϕ 1 0 ] ∈ R 4 x 4 } se(3)=\{ \xi =\left[{\rho \\, \phi } \right] \in \mathbb R^6,\rho \in \mathbb R^3,\xi ^∧ =\left[\begin{matrix} &0 & -\phi_3 &\phi_2 \\ &\phi_3 &0 &-\phi_1 \\ &-\phi_2 & \phi_1 &0\end{matrix} \right] \in \mathbb R^{4x4} \} se(3)={ξ=[ρ,ϕ]∈R6,ρ∈R3,ξ∧=⎣⎡​​0ϕ3​−ϕ2​​−ϕ3​0ϕ1​​ϕ2​−ϕ1​0​⎦⎤​∈R4x4}

se(3)中的每个元素$\xi$,是一个六维向量.前三维$\rho$表示平移;后三维$\varphi$表示旋转,本质上是so(3)元素.

在这里同样使用^符号将六维向量扩展成为四维矩阵,但不再表示反对称
KaTeX parse error: Expected '}', got '&' at position 41: …atrix}{\phi^ ∧ &̲\rho \\ 0^T ,& …
李代数se(3)的李括号和so(3)类似:
$$[{\xi }_1,{\xi }_2]=({\xi }_1^{\wedge }{\xi }_2^{\wedge }-{\xi }_2^{\wedge }{\xi }_1^{\wedge }{)}^{\vee }$$
se(3)和SE(3)间映射关系为
李群 $ T=exp(ξ∧) $

李代数 $\xi = ln(T) ^{∨} $

ch04-02 李群与李代数的转换关系:指数映射和对数映射

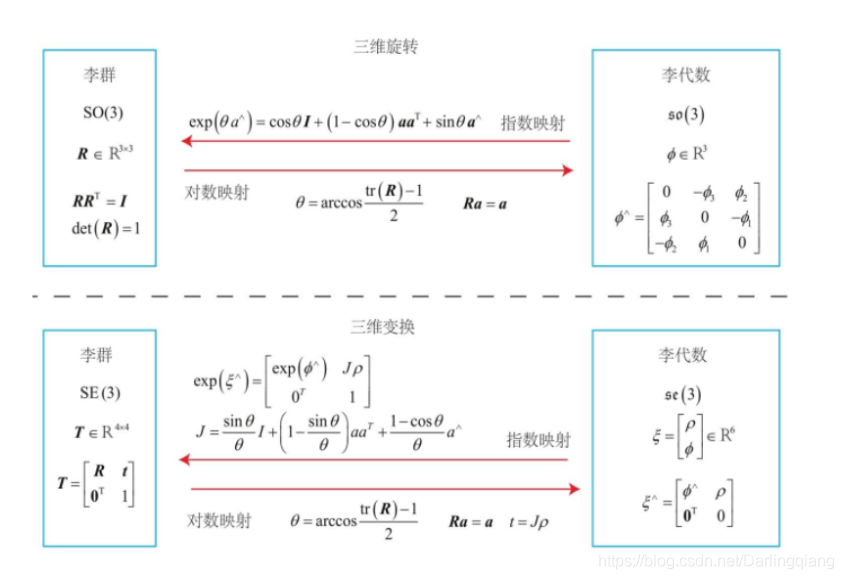
1. SO(3)和so(3)间的转换关系

将三维向量ϕ 分解为其模长θ和方向向量$ \alpha$,即ϕ = θ α .则从so(3)到SO(3)的指数映射可表示为:
$$R=exp(\varphi )=exp(\theta \alpha \wedge )=cos\theta I+(1-cos\theta )\alpha \alpha T+sin\theta \alpha \wedge$$
上式即为旋转向量到旋转矩阵的罗德里格斯公式,可见so(3)本质上是旋转向量组成的空间.

从SO(3)到so(3)的对数映射可表示为:
$$\varphi =ln(R{)}^V$$
实际计算时可以通过迹的性质分别求出转角θ和转轴α
$$\theta =arccos\frac{tr(R)-1}{2},R\alpha =\alpha$$

2.SE(3)和se(3)间的转换关系

从se(3)到SE(3)的指数映射可表示为:
$$T=exp({\xi }^{\wedge })=\left[\begin{array}{cc}R& J\rho \\ 0^T,& 1\end{array}\right]$$
$$J=\frac{sin\theta }{theta}I+(1-\frac{sin\theta }{\theta }\alpha {\alpha }^T)+(1-\frac{cos\theta }{\theta }{\alpha }^{\wedge })$$
可以看到,平移部分经过指数映射之后,发生了一次以J 为系数矩阵的线性变换.

3. 从SE(3)到se(3)的对数映射可表示为:

$$\xi =ln(T{)}^{\vee }$$

实际计算时ϕ 可以由SO(3)到so(3)的映射得到,ρ 可以由t = J ρ计算得到.

ch04-03 李代数求导: 引入李代数的一大动机就是方便求导优化

1. 群乘法与李代数加法的关系

BCH公式及其近似形式

1. 很遗憾地,李群乘积和李代数加法并不等价,即:
   $$R_1{R}_2=exp({\varphi }_1^{\wedge })exp({\varphi }_2^{\wedge })\ne exp((\varphi 1+\varphi 2)\wedge )$$
   李群乘积与李代数运算的对应关系由BCH公式给出:
   $$ln(exp(A)exp(B))=A+B+21[A,B]+121[A,[A,B]]-121[B,[A,B]]+...$$
   上式中[ , ] [,][,]表示李括号运算.

2. 当${\varphi }_1$ 或ϕ 2 为小量时,可以对BCH公式进行线性近似,得到李群乘积对应的李代数的表达式:

   R1⋅R2对应的李代数
   $$\begin{gathered} =ln(exp({\varphi }_1^{\wedge })exp({\varphi }_1^{\wedge }){)}^{\vee } \\ \approx J_l({\varphi }_2{)}^{-1}{\varphi }_1+{\varphi }_2(if{\varphi }_1->min) \\ \approx J_l({\varphi }_1{)}^{-1}{\varphi }_2+{\varphi }_1(if{\varphi }_2->min) \end{gathered}$$
   $$
   其中左乘雅可比矩阵$J_l$,即为从SE(3)到se(3)对数映射中的雅可比矩阵

$$J_l=\frac{sin\theta }{\theta }I+（1-\frac{sin\theta }{\theta }\alpha {\alpha }^T+\frac{1-cos\theta }{\theta }{\alpha }^{\wedge }）$$

其逆为
$$J_l^{-1}=\frac{\theta }{2}cot\frac{\theta }{2}I+(I-\frac{\theta }{2}cot\frac{\theta }{2})\alpha {\alpha }^T+\frac{\theta }{2}{\alpha }^{\wedge }$$
右乘雅可比矩阵只需对自变量取负号即可
$$J_r(\varphi )=J_r(-\varphi )$$
3. 李群SO(3)乘法与李代数so(3)加法的关系:

对旋转R (李代数为ϕ)左乘一个微小旋转ΔR(李代数为Δϕ),得到的旋转李群ΔR⋅R对应的李代数为:
$$=ln(exp(\Delta {\varphi }^{\wedge })exp(\Delta {\varphi }^{\wedge }))=\varphi +J_l^{-1}(\varphi )\Delta \varphi$$
反之,李代数加法(ϕ+Δϕ)对应的李群元素可表示为:
$$exp((\varphi +\Delta \varphi {)}^{\wedge }))=exp((J_l\Delta \varphi {)}^{\wedge })exp(\varphi {)}^{\wedge }))=exp(\varphi {)}^{\wedge }exp((J_r\Delta \varphi {)}^{\wedge })$$
4. 同理,李群SE(3)乘法与李代数se(3)加法的关系:
5.

$$\begin{gathered} exp(\Delta {\xi }^{\wedge })exp({\xi }^{\wedge })\approx exp((J_l^{-1}\Delta \xi +\xi {)}^{\wedge }) \\ exp({\xi }^{\wedge })exp(\Delta {\xi }^{\wedge })\approx exp((J_r^{-1}\Delta \xi +\xi {)}^{\wedge }) \end{gathered}$$

2. SO(3)上的李代数求导

对空间点p进行旋转,得到Rp,旋转之后点的坐标对旋转的导数可表示为:
$$\frac{\phi (Rp)}{\phi (R)}$$
对于上式的求导,有两种方式:

1.用李代数ϕ表示姿态R,然后根据李代数加法对ϕ 求导.

2.用李代数φ 表示微小扰动∂ R ,然后根据李群左乘对φ 求导.
其中扰动模型表达式简单,更为实用.

李代数求导

用李代数ϕ 表示姿态R,求导得到
$$\frac{\phi (Rp)}{\phi (R)}=\frac{\phi (exp(\varphi {)}^{\wedge }p}{\phi (\varphi )}$$

扰动模型(左乘)

另一种求导方式是对R进行一次左乘扰动∂R,设左乘扰动∂R对应的李代数为φ,对φ求导,得到
$$\frac{\phi (Rp)}{\phi (R)}=\frac{exp((\varphi +\phi {)}^{\wedge })p-exp({\varphi }^{\wedge })p}{\phi }=-(Rp{)}^{\wedge }$$

3. SE(3)上的李代数求导

类似地,空间点p经过变换T得到Tp,给T左乘一个扰动$\Delta T=exp(\delta {\xi }^{\wedge })$,则有
KaTeX parse error: Undefined control sequence: \matrix at position 43: …(\xi)} =\left[ \̲m̲a̲t̲r̲i̲x̲{I&-(Rp+t)^{∧} …

ch05 相机与图像

ch05-01 针孔相机模型

O−x−y−z为相机坐标系,现实空间点 P 的相机坐标为$[X,Y,Z]^T $,投影到O\prime -x\prime -y\prime 平面上的点P^{\prime },坐标为$[X’,Y’,Z’]^T$.

将成像平面对称到相机前方,根据几何相似关系$\frac{Z}{f}=\frac{X}{X^{{}^{\prime }}}=\frac{Y}{Y^{{}^{\prime }}}$ ,整理得到投影点P ′ 在投影平面上的坐标$P^{\prime }=[X^{\prime },Y^{\prime }]$

$$\{\begin{array}{r}{X}^{{}^{\prime }}=f\frac{X}{Z}\\ Y^{{}^{\prime }}=f\frac{Y}{Z}\end{array}$$
转换得到投影点P ′ 在像素平面上的像素坐标$P_{u,v}=[u,v{]}^T$
$$\{\begin{array}{r}u=\alpha X^{{}^{\prime }}+c_x=f_x\frac{X}{Z}+c_x\\ v=\beta Y^{{}^{\prime }}+c_y=f_y\frac{Y}{Z}+c_y\end{array}$$
其中，$u,v,c_x,c_y,f_x,f_y$的单位为像素,$\alpha ,\beta$的单位为像素/米.

将上式写成矩阵形式,得到**现实空间点相机坐标P和投影点像素坐标$P_{uv}\ast \ast$之间的关系:
$$Z{P}_{uv}=\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]\left[\begin{array}{ccc}{}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\triangleq KP$$

其中矩阵K称为相机的内参数矩阵.

上式中的P 为现实空间点在相机坐标系下的相机坐标,将其转为世界坐标$p_w$,有
$$Z{P}_{uv}=K(R{P}_w+t)=KT{P}_w$$
因此R ,t (或T )又称为相机的外参数.
将最后一维进行归一化处理,得到点P PP在归一化平面的归一化坐标 $P c = [ X / Z , Y / Z , 1 ] ^T $
$$P_c=\frac{P}{Z}=K^{-1}{P}_{uv}$$

参数矩阵有内参数K和外参数R,t,其中:

内参数矩阵K体现了归一化相机坐标到像素坐标的变换.

之所以是归一化坐标,这体现了投影性质:在某一条直线上的空间点,最终会投影到同一像素点上.

外参数矩阵R ,t (或T)体现了世界坐标到相机坐标的变换.

ch05-02 畸变模型

畸变包含两种: 径向畸变和切向畸变.

• 径向畸变: 由透镜形状引起,主要包括桶形畸变和枕形畸变.

  可以看成坐标点沿着长度方向发生了变化,也就是其距离原点的长度发生了变化.
  $$\begin{gathered} x_{distorted}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6) \\ {y}_{distorted}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6) \end{gathered}$$
  切向畸变: 由透镜和成像平面不严格平行引起.

  可以看成坐标点沿着切线方向发生了变化，也就是水平夹角发生了变化.

$$\begin{gathered} x_{distorted}=x+2p_{1}xy+p_2(r^2+2x^2) \\ {y}_{distorted}=y+p_1(r^2+2y^2)+2p_{2}xy \end{gathered}$$

ch05-03 单目相机的成像过程

单目相机的成像过程：

• 1. 世界坐标系下有一个固定的原点P,其世界坐标$P_w$
• 2. 由于相机在运动,它的运动由R ,t 或变换矩阵$T\in SE(3)$描述.原点P的相机坐标$P_c^{{}^{\prime }}=R{P}_w+t$
• 3. 这时$P_c^{{}^{\prime }}$的分量为X,Y ,Z ,把它们投影到归一化平面Z =1上,得到P 的归一化相机坐标$\frac{P_c^{{}^{\prime }}}{Z}=[\frac{X}{Z},\frac{Y}{Z},1]$
• 4. 有畸变时,根据畸变参数计算$P_c$发生畸变后的归一化相机坐标
• 5. P的归一化相机坐标经过内参K后,对应到它的像素坐标$P_{uv}=K{P}_c$

在讨论相机成像模型时,我们一共谈到了四种坐标: 世界坐标、相机坐标、归一化相机坐标和像素坐标.请读者厘清它们的关系,它反映了整个成像的过程.

ch06 非线性优化

ch06-01 状态估计问题

最大后验与最大似然

SLAM模型由状态方程和运动方程构成:
$$\{\begin{array}{r}{x}_k=f(x_{k-1},u_k,w_k)\\ z_{k,j}=h(y_j,x_k,v_{k,j})\end{array}$$
通常假设两个噪声项$w_k,v_{k,j}$满足零均值的高斯分布:
$$w_k\sim N(0,R_k),v_{k,j}\sim N(0,Q_{k,j})$$
对机器人的估计,本质上就是已知输入数据u 和观测数据z 的条件下,求机器人位姿x 和路标点y 的条件概率分布:
$$P(x,y|z,u)$$
利用贝叶斯法则,有:
$$P(x,y|z,u)=\frac{P(z,u|x,y)}{P(z,u)}\propto P(z,u|x,y)P(x,y)$$
其中，$P(x,y|z,u) $ 为后验概率 $P(z,u|x,y)$为似然$P(x,y)$为先验,上式可表述为后验概 率 ∝ 似 然 ⋅ 先 验 后 直接求后验分布是困难的,但是求一个状态最优估计,使得在该状态下后验概率最大化则是可行的:
$$(x,y{)}_{MLE}^{\ast }=argmaxP(x,y\mid z,u)$$
最大似然估计的直观意义为:在什么样的状态下，最可能产生现在观测到的数据.

ch06-02 最小二乘

基于观测数据z zz的最小二乘

对于某一次观测
$$z_{k,j}=h(y_j,x_k)+v_{k,j}$$
由于假设噪声$v k , j ∼ N ( 0 , Q k , j ) $则观测数据$z_{j,k}$的似然为
$$P(z_{j,k}|x_k,y_J)=N(h(y_j,x_k),Q_{k,j})$$
将上式代入高斯分布表达式中,并取负对数,得到
$$\begin{gathered} (x_k,y_j{)}^{\ast }=argmaxN(h(y_j,x_k),Q_{k,j}) \\ =argmin(z_{k,j}-h(x_k,y_j){)}^T{Q}_{k,j}^{-1}(z_{k,j}-h(x_k,y_j)) \end{gathered}$$
上式等价于最小化噪声项(即误差)的一个二次型,其中$Q_{k,j}^{-1}$称为信息矩阵,即高斯分布协方差矩阵的逆.

基于观测数据z 和输入数据u 的最小二乘
因为观测z 和输入u 是独立的,因此可对z 和u 的联合似然进行因式分解:
$$P(x,y|z,u)=\prod _{k}P(u_k|x_{k-1},x_k)\prod P(z_{j,k}|x_k,y_j)$$
定义输入和观测数据与模型之间的误差:
$$\begin{gathered} e_{u,k}=x_k-f(x_{k-1},u_k) \\ {e}_{z,j,k}=z_{k,j}-h(x_k,y_j) \end{gathered}$$
定义
$$J(x,y)=\sum _k{e}_{u,k}^T{R}_k^{-1}{e}_{u,k}+\sum _k\sum _j{e}_{k,j}^T{Q}_{k,j}^{-1}{e}_{z,k,j}$$
则有
$$(x_k,y_j{)}^{\ast }=argminJ(x,y)$$

ch06-03 非线性最小二乘

对于非线性最小二乘问题:
$$mi{n}_{x}F(x)=\frac{1}{2}||f(x)|{|}_2^2$$
求解该问题的具体步骤如下:

• 1. 给定某个初始值$x_0$
• 2. 对于第k次迭代,寻找一个增量$\Delta x_k$,使得$F(x_k+\Delta x_k)$达到极小值
• 3. 若$\Delta x_k$足够小,则停止
• 4. 否则 ，令$x_{k+1}=x_k+\Delta x_k$,返回第2步$x_{k+1}=x_k+\Delta x_k$,返回第2步

这样,最小二乘问题被转化为一个不断寻找下降增量$\Delta x_k$的问题.,具体有以下方法

常见方法有 最速下降法，牛顿法，高斯牛顿法，LM法

1. 一阶梯度法(一阶梯度又称最速下降法)和二阶梯度法（牛顿法）

目标函数$F(x)$在$x_k$附近的Tayor展开
$$F(x+\Delta x_k)\approx F(x_k)+J(x_k{)}^T\Delta x_k+\frac{1}{2}\Delta x_k^{T}H(x_k)x_k$$
其中$J(x)$是F(x)关于x的一阶导数矩阵,H(x)是F(x)关于x 的二阶导数矩阵.

其中若$\Delta x_k$ 取一阶导数,则
$$\Delta x_k^{\ast }=-J(x_k)$$
其中若$\Delta x_k$ 取2阶导数,则
$$\Delta x_k^{\ast }=argmin(F(x_k)+J(x_k{)}^T\Delta x_k+\frac{1}{2}\Delta x_k^{T}H(x_k)x_k)$$
令上市对$\Delta x_k$ 导数为0，则求得
$$H\Delta x_k=-J$$

2. 高斯牛顿法

将$f(x)$在$X_k$附近进行泰勒展开 得
$$f(x_k+\Delta x_k)\approx f(x_k)+J(x_k)\Delta x_k$$
则
$$\Delta x_k^{\ast }=argmi{n}_{\Delta }{x}_k\frac{1}{2}||f(x_k)+J(x_k{)}^T\Delta x_k|{|}^2$$
令上式对$\Delta x$的导数为0,得到高斯牛顿方程
$$J(x_k)f(x_k)+J(x_k)J(x_k{)}^T\Delta x_k=0$$
令 $H(x)=J(x_k)J(x_k{)}^T,g(x)=-J(x)f(x)$，则$\Delta x_k^{\ast }$ 可以取 $H\Delta x_k=g$ 的解 .

3.列文伯格-马夸尔特方法

泰勒展开只能在展开点附近才有较好的近似效果,因此应给$\Delta x$添加一个范围,称为信赖区域.

定义一个指标$\rho$刻画这个近似的好坏程度,其分子为实际函数下降的值,分母是近似模型下降的值:
$$\rho =\frac{f(x+\Delta x)-f(x)}{J(x{)}^T\Delta x}$$
通过调整$\rho$来确定信赖区域:

若$\rho$接近1,则近似是最好的.
若$\rho$太小,说明实际下降的值远小于近似下降的值,则认为近似比较差,需要缩小近似范围.
若$\rho$太大,说明实际下降的比预计的更大,我们可以放大近似范围.

列文伯格-马夸尔特方法算法步骤如下：

• step 1:给定初始值$x_0$ ,以及初始优化半径$\mu$

• step 2:对于第k 次迭代,求解:
  $$\begin{gathered} mi{n}_{\Delta x_k}\frac{1}{2}||f(x_k)+J(x_k{)}^T\Delta x_k|{|}^2 \\ \text{s.t.}||D\Delta x_k|{|}^2\le \mu \end{gathered}$$
  其中,$\mu$是信赖区域的半径,D 为系数矩阵

• step 3: 计算ρ

• step 4: $\rho >\frac{3}{4}$ ，则$\mu =2\mu$

• step 5:$\rho <\frac{1}{4}$ ，则$\mu =0.5\mu$

• step 6: 若ρ大于某阈值,则认为近似可行.令 $x_{k+1}=x_k+\Delta x_k$

• step 7:判断算法是否收敛.如不收敛则返回第2步,否则结束.

在step 2步中$\Delta x_k$的求解要使用拉格朗日乘数法:
$$L(\Delta x_k,\lambda )=\frac{1}{2}||f(x_k)+J(x_k{)}^T\Delta x_k|{|}^2+\frac{\lambda }{2}(||D\Delta x_k|{|}^2-\mu )$$
令上式对$\Delta x_k$导数为0,得到
$$(H+\lambda D^{T}D)\Delta x_k=g$$
考虑简化形式,即D=I,则相当于求解
$$(H+\lambda I)\Delta x_k=g$$
当λ较小时,H占主要地位,这说明二次近似模型在该范围内是比较好的,列文伯格-马夸尔特方法更接近于高斯牛顿法.
当λ 比较大时,$\lambda I$占据主要地位,这说明二次近似模型在该范围内不够好,列文伯格-马夸尔特方法更接近于一阶梯度下降法.

ch07 视觉里程计01

ch07 -01 特征点匹配

特征点:根据特征点匹配计算相机运动
根据特征点匹配计算相机运动.根据相机的成像原理不同,分为以下3种情况：

• 当相机为单目时,我们只知道匹配点的像素坐标,是为2D-2D匹配,使用对极几何求解.以及弹幕初始化的过程。
• 当相机为双目或RGB-D时,我们就知道匹配点的像素坐标和深度坐标,是为3D-3D匹配,使用ICP求解.
• 如果有3D点及其在相机的投影位置,也能估计相机的运动,是为3D-2D匹配,使用PnP求解.

ch07 -02 2D-2D匹配: 对极几何

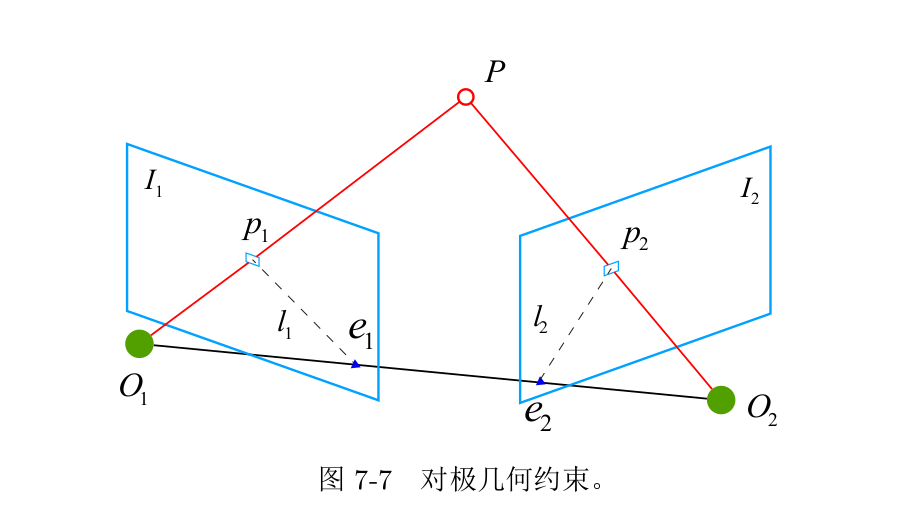
考虑从两张图像上观测到了同一个3D点，如图所示**。**我们希望可以求解相机两个时刻的运动$R,t$。

假设我们要求取两帧图像$I_1,I_2$之间的运动,设第一帧到第二帧的运动为R ,t,两个相机中心分别为$O_1,O_2$.考虑$I_1$中有一个特征点$p_1$,它在$I_2$中对应着特征点$p_2$.连线$\overrightarrow{O_1 p_1} $和$\overrightarrow{O_2 p_2}$ 在三维空间中交于点P,这时点$O_1,O_2,P$三个点可以确定一个平面,为极平面.$O_1,O_2$连线与像平面$I_1,I_2$的交点分别为$e_1,e_2$,$e_1,e_2$称为极点,$O_1{O}_2$称为基线，极平面与两个像平面$I_1,I_2$之间的相交线$l_1,l_2$称为极线.

$P$在$I_1$下的线号机坐标为$P=[X,Y,Z{]}^T$,两个投影像素点$p_1,p_2$ 的像素位置满足如下公式：
$$\{\begin{array}{r}{s}_1{p}_1=KP\\ s_2{p}_2=K(RP+t)\end{array}$$
取 $p_1,p_2$ 的归一化坐标$\{\begin{array}{r}{x}_1=K^{-1}{p}_1\\ x_2=K^{-1}{p}_2\end{array}$

$x_1,x_2$是两个像素归一化平面上的坐标。代入上式，得到$x_2=R{x}_1+t$

同时左乘 $t^{\wedge }$可得：
$$t^{\wedge }{x}_2=t^{\wedge }R{x}_1$$
同时左乘 $x_2^T$,可得
$$x_2^T{t}^{\wedge }{x}_2=x_2^T{t}^{\wedge }R{x}_1$$
可得
$$x_2^T{t}^{\wedge }R{x}_1=0$$
重新带入$p_1,p_2$，可得：
$$p_2^T{K}^{-T}{t}^{\wedge }R{K}^{-1}{p}_1=0$$
以上俩个式子称为对极约束,定义基础矩阵F和本质矩阵E,可以进一步简化对极约束:
$$E=t^{\wedge }RF=K^{-T}E{K}^{-1}{x}_2^{T}E{x}_1=p_2^{T}F{p}_1=0$$
本质矩阵E 的求解
考虑到E 的尺度等价性,可以用8对点来估计E,是为八点法.

对于一对匹配点,其归一化坐标$x_1=[u_1,v_1,1],x_2=[u_2,v_2,1]$根据对极约束,有
$$(u_1,v_1,1)\left[\begin{array}{ccc}{e}_1& e_2& e_3\\ e_4& e_5& e_6\\ e_7& e_8& e_9\end{array}\right]\left[\begin{array}{c}{u}_2\\ v_2\\ 1\end{array}\right]=0$$

把矩阵E展开为向量${\left[\begin{array}{ccccccccc}{e}_1& e_2& e_3& e_4& e_5& e_6& e_7& e_8& e_9\end{array}\right]}^T$ ,对极约束可以写成与e ee有关的线性形式:
$$[u_1{u}_2,u_1{v}_2,u_1,v_1{u}_2,v_1{v}_2,v_1,u_2,v_2,1{]}^T.e=0$$
把八对点对应的$x_1,x_2$分别代入方程中,得到线性方程组:

求得E后,对E进行SVD分解以求取R,t :设E的SVD分解为$E=U\sum V^T$则对应的R ,t 分别为:
$$t^{\wedge }=U{R}_Z(\frac{\pi }{2})\sum U^{T}R=U{R}_Z^T(\frac{\pi }{2})\sum V^T$$
其中$R_Z(\frac{\pi }{2})$表示沿Z轴旋转90°得到的旋转矩阵.

对极几何的讨论:

• 1. 尺度不确定性: 2D图像不具有深度信息,这导致了单目视觉的尺度不确定性. 实践中设t 为单位1,计算相机运动和和特征点的3D位置,这被称为单目SLAM的初始化.

  2. 退化问题：当特征的共面或者相机发生纯旋转时，基础矩阵的自由度下降，就出现所谓的退化。实际中数据总是包含一些噪声，这时候继续使用八点法求解基础矩阵，基础矩阵多余出来的自由度将会主要由噪声决定。

     为了可以避免退化现象造成的影响，通常在估计基础矩阵F的同时会求解单应矩阵H，选择重投影误差比较小的那个作为最终的运动估计矩阵。

  3. 初始化的纯旋转问题: 若相机发生纯旋转,导致t 为零,得到的E也将为零,会导致我们无从求解R.因此单目初始化不能只有纯旋转,必须要有一定程度的平移.

  4. 多于8对点的情况:

     对于八点法,有$Ae=0$,其中A为一个8×9的矩阵.

     若匹配点的个数多于8个,A的尺寸变化,上述方程不成立.因此转而求取最小化二次型
     $$mi{n}_e||Ae|{|}_2^2=mi{n}_e{e}^T{A}^{T}Ae$$
     是为最小二乘意义下的E EE矩阵.

ch07 -03 3D-2D匹配: PnP(Perspective-n-Point)

2D-2D的对极几何方法需要8个或8个以上的点对（以八点法为例），且存在着初始化、纯旋转和尺度的问题。然而，如果两张图像中其中一张特征点的3D位置已知，那么最少只需3个点对（需要至少一个额外点验证结果）就可以估计相机运动。

在双目或RGB-D的视觉里程计中，我们可以直接使用PnP估计相机运动。而在单目视觉里程计中，必须先进行初始化，然后才能使用PnP。

PnP问题有多种解决方法:

• 直接线性表变换(DLT): 先求解相机位姿,再求解空间点位置
• P3P: 先求解空间点位置,再求解相机位姿
• Bundle Adjustment: 最小化重投影误差,同时求解空间点位置和相机位姿

1. 直接线性变换(DLT): 先求解相机位姿,再求解空间点位置**

考虑某个空间点P的齐次世界坐标为$P=(X,Y,Z,1)$ .在图像$I_1$中投影到特征点的归一化像素坐标$x_1=(u_1,v_1,1)$.此时相机的位姿R ,t 是未知的,定义增广矩阵$[R|t]$(不同于变换矩阵T TT)为一个3×4的矩阵,包含了旋转与平移信息,展开形式如下:
$$s\left(\begin{array}{c}{u}_1\\ v_1\\ 1\end{array}\right)=\left(\begin{array}{cccc}{t}_1& t_2& t_3& t_4\\ t_5& t_6& t_7& t_8\\ t_9& t_{1}0& t_{1}1& t_{1}2\end{array}\right)\left(\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right)$$

用最后一行把s消去,得到两个约束:
$$\{\begin{array}{r}{t}_1^{T}P-t_3^{T}P{u}_1=0\\ t_2^{T}P-t_3^{T}P{v}_1=0\end{array}$$
其中$t_1=(t_1,t_2,t_3,t_4)$,$t_2=(t_5,t_6,t_7,t_8)$,$t_3=(t_9,t_{1}0,t_{1}1,t_{1}2)$.$t_1,t_2,t_3$为待求量.

将N对匹配的特征点代入方程中,得到线性方程组:
$$\left(\begin{array}{ccc}{P}_1^T& 0& -U_1{P}_1^T\\ 0& P_1^T& -U_1{P}_1^T\\ P_N^T& 0& -U_N{P}_N^T\\ 0& P_N^T& -U_N{P}_N^T\end{array}\right)$$

只需6对匹配点即可求解增广矩阵[ R ∣ t ] ,若匹配点数多于6对时,可以求最小二乘解.对于求解出的旋转矩阵R,可以通过QR分解等手段将其投影到S E ( 3 ) 上.

2. P3P: 先求解空间点位置,再求解相机位姿

这里要说明的是在场景1中，我们通常输入的是物体在世界坐标系下的3D点以及这些3D点在图像上投影的2D点，因此求得的是相机（相机坐标系）相对于真实物体（世界坐标系）的位姿，如图所示：

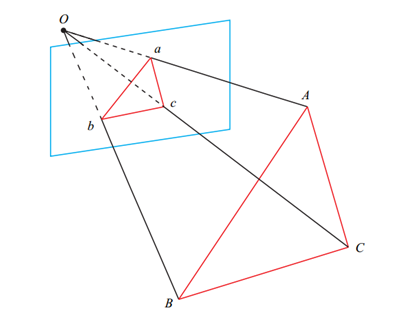
而在场景2中，通常输入的是上一帧中的3D点（在上一帧的相机坐标系下表示的点）和这些3D点在当前帧中的投影得到的2D点，所以它求得的是当前帧相对于上一帧的位姿变换，如图所示：

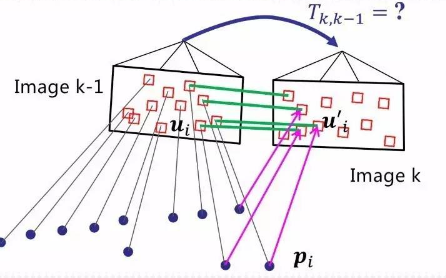
两种情况本质上是相同的，都是基于已知3D点和对应的图像2D点求解相机运动的过程。下面详细探讨P3P的求解过程。

已知3对匹配点的世界坐标A ,B ,C 和投影坐标a ,b ,c ,根据三角形的余弦定理,有
$$\{\begin{array}{r}O{A}^2+O{B}^2-2OA\cdot OB\cdot cos<a,b>=A{B}^2\\ O{B}^2+O{C}^2-2OB\cdot OC\cdot cos<b,c>=B{C}^2\\ O{A}^2+O{C}^2-2OA\cdot OC\cdot cos<a,c>=A{C}^2\end{array}$$
记$x=OA/OC,y=OB/OC,u=B{C}^2/A{B}^2,v=A{C}^2/A{B}^2$
$$\{\begin{array}{r}(1-u)y^2-u{x}^2-cos<b,c>y+2uxycos<a,b>+1=0\\ (1-w)x^2-w{y}^2-cos<a,c>y+2wxycos<a,b>+1=0\end{array}$$
上式中,三个余弦角$\cos ⟨a,b⟩,\cos ⟨b,c⟩,\cos ⟨a,c⟩$以及u uu,v vv是已知的,可以求解出x ,y 进而求解出A ,B ,C 三点的相机坐标.然后根据3D-3D的点对,计算相机的运动R ,t .

3. Bundle Adjustment: 最小化重投影误差,同时求解空间点位置和相机位姿

设相机位姿变换矩阵T ,某空间点的世界坐标 $P_i=[X,Y,Z{]}^T$, 其投影的像素坐标为 $u_i=[u_i,v_i{]}^T$ ,像素位置与空间点位置的关系如下:
$$s_i{u}_i=KT{P}_i$$
由于相机位姿未知及观测点的噪声,上式存在一个误差,称为重投影误差$ \displaystyle e=u_i-\frac{1}{s_i}KTP_i$因此我们对重投影误差求和,寻找最好的相机位姿和特征点的空间位置,最小化重投影误差:
$$\begin{gathered} T^{\ast }=argmi{n}_T\frac{1}{2}\sum _{i=1}^n||u_i-\frac{1}{s_i}KT{P}_i|{|}^2 \\ {P}_i^{\ast }=argmi{n}_{P_i}\frac{1}{2}\sum _{i=1}^n||u_i-\frac{1}{s_i}KT{P}_i|{|}^2 \end{gathered}$$
使用最小二乘优化,要分别求e对T和P的导数:
$$e(x+\Delta x)\approx e(x)+J\Delta x$$

• 求e 对T 的导数:当e为像素坐标误差(2维),x为相机位姿(6维)时,J将是一个2×6的矩阵.我们来推导J的形式:

  取中间变量$P^{\prime }=(TP{)}_{1:3}=[X^{\prime },Y^{\prime },Z^{\prime }{]}^T$使用李代数求导的扰动模型,对T左乘微小扰动$\delta \xi$,求导得到:
  $$\frac{\partial e}{\partial \delta \xi }=li{m}_{\delta \xi =0}\frac{e(\delta \xi \oplus \xi )-e(\xi )}{\delta \xi }=\frac{\partial e}{\partial P^{‘}}\frac{\partial P^{‘}}{\partial \delta \xi }$$
  其中，$\oplus $ 表示李代数的左乘扰动 ,其中 第一项 $ \displaystyle \frac{\partial e}{\partial P^{‘}}$:

  该误差表示误差关于投影点的导数：
  $$\frac{\partial e}{\partial P^{‘}}=-\left(\begin{array}{ccc}\frac{\partial u}{\partial X^{‘}}& \frac{\partial u}{\partial Y^{‘}}& \frac{\partial u}{\partial Z^{‘}}\\ \frac{\partial v}{\partial X^{‘}}& \frac{\partial v}{\partial Y^{‘}}& \frac{\partial v}{\partial Z^{‘}}\end{array}\right)=-\left(\begin{array}{ccc}\frac{f_x}{Z^{‘}}& 0& -\frac{f_x{X}^{‘}}{Z^{‘2}}\\ 0& \frac{f_y}{Z^{‘}}& -\frac{f_x{Y}^{‘}}{Z^{‘2}}\end{array}\right)$$
  第二项$\frac{\partial P^{‘}}{\partial \delta \xi }$ 为变换后的点关于李代数的导数:
  $$\frac{\partial P^{‘}}{\partial \delta \xi }=\frac{TP}{\partial \delta \xi }=(TP{)}^{⨀}=\frac{\partial e}{\partial P^{‘}}=-\left(\begin{array}{cc}I& -P\\ 0^T& 0^T\end{array}\right)$$
  而在$P^{{}^{\prime }}$的定义中，取出前3维，于是得到：$\frac{\partial P^{‘}}{\partial \delta \xi }=\frac{TP}{\partial \delta \xi }=(TP{)}^{⨀}=[I,-P]$

  而
  $$\left(\begin{array}{}\end{array}\right)$$
  $$P^{{}^{\prime }\wedge }=\left(\begin{array}{ccc}0& Z^{{}^{\prime }}& -Y^{{}^{\prime }}\\ -Z^{{}^{\prime }}& 0& X^{{}^{\prime }}\\ Y^{{}^{\prime }}& -X^{{}^{\prime }}& 0\end{array}\right)$$

  将两项相乘,得到了2×6的雅可比矩阵$J^T$,求e 对P的导数可得结果如下：
  $$J^T=\frac{\partial e}{\partial \delta \xi }=\left(\begin{array}{cccccc}\frac{f_x}{Z^{‘}}& 0& -\frac{f_x{X}^{‘}}{Z^{‘2}}& -\frac{f_x{X}^{‘}{Y}^{‘}}{Z^{‘2}}& f_x+\frac{f_x{X}^{‘2}}{Z^{‘2}}& -\frac{f_x{Y}^{‘}}{Z^{‘}}\\ 0& \frac{f_Y}{Z^{‘}}& -\frac{f_y{Y}^{‘}}{Z^{‘2}}& -f_y-\frac{f_{y}Y{X}^{‘2}}{Z^{‘2}}& \frac{f_y{Y}^{‘}{X}^{‘}}{Z^{‘2}}& \frac{f_y{X}^{‘}}{Z^{‘}}\end{array}\right)$$

  **该Jocabi矩阵描述了，重投影误差关于相机位姿李代数的一阶变化关系。**前面有负号的原因是 该误差由观测值减预测值得到。

  特征点位置的优化，需要求解e对空间点P的导数，由链式法则可得：
  $$\frac{\partial e}{\partial P}=\frac{\partial e}{\partial P^{‘}}\frac{\partial P^{‘}}{\partial P}$$
  第一项误差关于投影点的导数已经得到，关于第二项$\frac{\partial P^{‘}}{\partial P}$，按照定义

$$P^{‘}=exp({\xi }^{\wedge })P=RP+t$$

求导后为可得：
$$P^{‘}=R$$
所所以$\frac{\partial e}{\partial P}$为：
$$\frac{\partial e}{\partial P}=-\left(\begin{array}{ccc}\frac{f_x}{Z^{‘}}& 0& -\frac{f_x{X}^{‘}}{Z^{‘2}}\\ 0& \frac{f_y}{Z^{‘}}& -\frac{f_x{Y}^{‘}}{Z^{‘2}}\end{array}\right)$$

小姐：

由以上两个大的步骤我们推导得到 观测相机方程关于相机位姿与特征点的两个导数矩阵。

4.EPnP求解位姿

详细见OPenCV提供的EPnP求PnP问题，然后通过G2O优化求解，见十四讲P165.

ch07 -04 3D-3D匹配: ICP

对于一组已配对好的3D点:
$$P=p_1,\cdots ,p_n,P\prime =p_1\prime ,\cdots ,p_n\prime$$
现在,想要找一个欧氏变换R ,t ,使得:
$$\forall i,p_i=R{p}_i\prime +t$$
ICP问题的求解包含两种方式:

1. 利用线性代数的求解(主要是SVD)
2. 利用非线性优化方式的求解(类似于Bundle Adjustment)

1. SVD方法

定义第 i对点的误差项为$e_i=p_i-(R{p}_i^{\prime }+t)$,定义两组点的质心$p=\frac{1}{n}{\sum }_{i=1}^n(p_i),p^{\prime }=\frac{1}{n}{\sum }_{i=1}^n(p_i^{\prime })$

构建最小二乘问题,求取最合适的 R, t.
$$\begin{gathered} mi{n}_{R,t}J=\frac{1}{2}||(p_i-((R{p}_i^{\prime }+t)))|{|}_2^2 \\ =\frac{1}{2}||(p_i-p-R(p_i^{\prime }-p^{\prime })|{|}^2+||p-R{p}^{\prime }-t|{|}^2 \end{gathered}$$
左边只和旋转矩阵R相关,而右边既有 R也有t,但只和质心相关.因此令左边取最小值解出R,代入到右边令式子等于0求出t.

定义去质心坐标$qi=pi-p,q_i^{\prime }=p_i^{\prime }-p^{\prime }$ 则优化目标可写成:
$$\begin{gathered} R^{\ast }=mi{n}_R\sum _{i=1}^n||(p_i-p-R(p_i^{\prime }-p^{\prime })|{|}^2 \\ =mi{n}_R\sum _{i=1}^n-q_i^{T}R{q}_i^{\prime } \\ =-tr(R\sum _{i=1}^n{q}_i^{\prime }{q}_i^T) \end{gathered}$$
省略数学证明,定义矩阵:
$$W=\sum _{i=1}^n{q}_i{q}_i^{{}^{\prime }T}$$
对矩阵W WW进行SVD分解得到:
$$W=U\Sigma VT$$
可求解
$$R=U{V}^T$$

2. 非线性优化方法

使用李代数表达表达位姿,目标函数可以写成
$$mi{n}_{\xi }=\frac{1}{2}\sum _{i-1}^n||(p_i-exp({\xi }^{\wedge })p^{\prime })|{|}_2^2$$
误差项关于位姿的导数可以用李代数求导的扰动模型,计算导数得到:
$$\frac{\partial P^{}}{\partial \delta \xi }=-(exp({\xi }^{\wedge })p_i^{\prime }{)}^{⨀}$$

对于一组已配对好的3D点:
$$P=p_1,\cdots ,p_n,P\prime =p_1\prime ,\cdots ,p_n\prime$$
现在,想要找一个欧氏变换R ,t ,使得:
$$\forall i,p_i=R{p}_i\prime +t$$
ICP问题的求解包含两种方式:

1. 利用线性代数的求解(主要是SVD)
2. 利用非线性优化方式的求解(类似于Bundle Adjustment)

3. SVD方法求解

定义第 i对点的误差项为$e_i=p_i-(R{p}_i^{\prime }+t)$,定义两组点的质心$p=\frac{1}{n}{\sum }_{i=1}^n(p_i),p^{\prime }=\frac{1}{n}{\sum }_{i=1}^n(p_i^{\prime })$

构建最小二乘问题,求取最合适的 R, t.
$$\begin{gathered} mi{n}_{R,t}J=\frac{1}{2}||(p_i-((R{p}_i^{\prime }+t)))|{|}_2^2 \\ =\frac{1}{2}||(p_i-p-R(p_i^{\prime }-p^{\prime })|{|}^2+||p-R{p}^{\prime }-t|{|}^2 \end{gathered}$$
左边只和旋转矩阵R相关,而右边既有 R也有t,但只和质心相关.因此令左边取最小值解出R,代入到右边令式子等于0求出t.

定义去质心坐标$qi=pi-p,q_i^{\prime }=p_i^{\prime }-p^{\prime }$ 则优化目标可写成:
$$\begin{gathered} R^{\ast }=mi{n}_R\sum _{i=1}^n||(p_i-p-R(p_i^{\prime }-p^{\prime })|{|}^2 \\ =mi{n}_R\sum _{i=1}^n-q_i^{T}R{q}_i^{\prime } \\ =-tr(R\sum _{i=1}^n{q}_i^{\prime }{q}_i^T) \end{gathered}$$
省略数学证明,定义矩阵:
$$W=\sum _{i=1}^n{q}_i{q}_i^{{}^{\prime }T}$$
对矩阵W WW进行SVD分解得到:
$$W=U\Sigma VT$$
可求解
$$R=U{V}^T$$

4. 非线性优化方法求解

使用李代数表达表达位姿,目标函数可以写成
$$mi{n}_{\xi }=\frac{1}{2}\sum _{i-1}^n||(p_i-exp({\xi }^{\wedge })p^{\prime })|{|}_2^2$$
误差项关于位姿的导数可以用李代数求导的扰动模型,计算导数得到:
$$\frac{\partial P^{}}{\partial \delta \xi }=-(exp({\xi }^{\wedge })p_i^{\prime }{)}^{⨀}$$
可以直接使用最小二乘优化方法求解位姿.