二叉树的遍历

已于 2024-09-01 21:43:38 修改
阅读量762 收藏 8
点赞数 18
CC 4.0 BY-SA版权
分类专栏： 算法与数据结构 文章标签： 算法 数据结构
于 2024-09-01 17:01:16 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/DaisyMaria/article/details/141164400

1.二叉树的先/中/后序遍历

先序遍历是一种深度优先遍历方法，其遍历顺序是：首先访问根节点，然后递归地访问左子树，最后递归地访问右子树。（根—左—右）

中序遍历：左—根—右

后序遍历：左—右—根

先解决【先序遍历】：

  1. 定义数据结构：首先，我们需要定义一个数据结构来表示二叉树的节点。每个节点包含两个指针，分别指向其左子节点和右子节点。
  2. 读取输入：接下来，我们从输入中读取二叉树的结构信息，并将其存储在我们定义的数据结构中。
  3. 递归遍历：我们定义一个递归函数preOrder，该函数接受一个节点编号作为参数。在函数内部，首先检查当前节点是否为-1，如果是，则直接返回；否则，将当前节点编号添加到pre列表中，然后递归调用preOrder函数访问左子节点和右子节点。
  4. 输出结果：在遍历过程中，我们将访问的节点编号存储在一个列表中，最后按顺序输出这个列表。
#include<cstdio>
#include<vector>
using namespace std;

const int MAXN = 50;

struct Node {
	int l, r;// 左子节点和右子节点编号
}nodes[MAXN];

vector<int> pre; // 存储先序遍历结果

void preOrder(int root) {
	if (root == -1) { // 如果当前节点为空，直接返回
		return;
	}

	pre.push_back(root); // 访问当前节点
	preOrder(nodes[root].l); // 递归访问左子树
	preOrder(nodes[root].r); // 递归访问右子树
}

int main()
{
	int n;
	scanf("%d", &n);

	for (int i = 0; i < n; i++)
	{
		scanf("%d%d", &nodes[i].l, &nodes[i].r);
	}

	preOrder(0);

	for (int i = 0; i < (int)pre.size(); i++)
	{
		printf("%d", pre[i]);
		if (i < (int)pre.size() - 1) {
			printf(" ");
		}
	}

	return 0;
}

先序遍历核心代码：（根—左—右）

vector<int> pre; // 存储先序遍历结果

void preOrder(int root) {
    if (root == -1) { // 如果当前节点为空，直接返回
        return;
    }

    pre.push_back(root); // 访问当前节点
    preOrder(nodes[root].l); // 递归访问左子树
    preOrder(nodes[root].r); // 递归访问右子树
}

 中序遍历核心代码：（左—根—右）

vector<int> in; // 存储中序遍历结果

void inOrder(int root) {
    if (root == -1) { // 如果当前节点为空，直接返回
        return;
    }

    inOrder(nodes[root].l); // 递归访问左子树
    in.push_back(root); // 访问当前节点
    inOrder(nodes[root].r); // 递归访问右子树
}

后序遍历核心代码：（左—右—根）

vector<int> post; // 存储后序遍历结果 

void postOrder(int root) {
    if (root == -1) { // 如果当前节点为空，直接返回
        return;
    }

    postOrder(nodes[root].l); // 递归访问左子树
    postOrder(nodes[root].r); // 递归访问右子树
    post.push_back(root); // 访问当前节点
}

2.二叉树的层序遍历

层序遍历是一种按照树的层次顺序，从上到下、从左到右访问每个节点的遍历方式。

为了实现这一目标，我们可以使用广度优先搜索（BFS）算法。BFS算法通常使用队列来辅助实现，能够确保我们按照层次顺序访问每个节点。

只需要对问题1.中核心代码进行修改即可

vector<int> layer; // 存储层序遍历结果

void layerOrder(int root)

{
    queue<int> q;//创建队列用于BFS
    q.push(root);//将根节点加入队列
    while (!q.empty())
    {
        int front = q.front();//取出队列头结点
        q.pop();
        layer.push_back(front);// 将节点编号加入层序遍历结果
        if (nodes[front].l != -1) {// 如果左子节点存在，加入队列
            q.push(nodes[front].l);
        }
        if (nodes[front].r != -1) {// 如果右子节点存在，加入队列
            q.push(nodes[front].r);
        }
    }
}

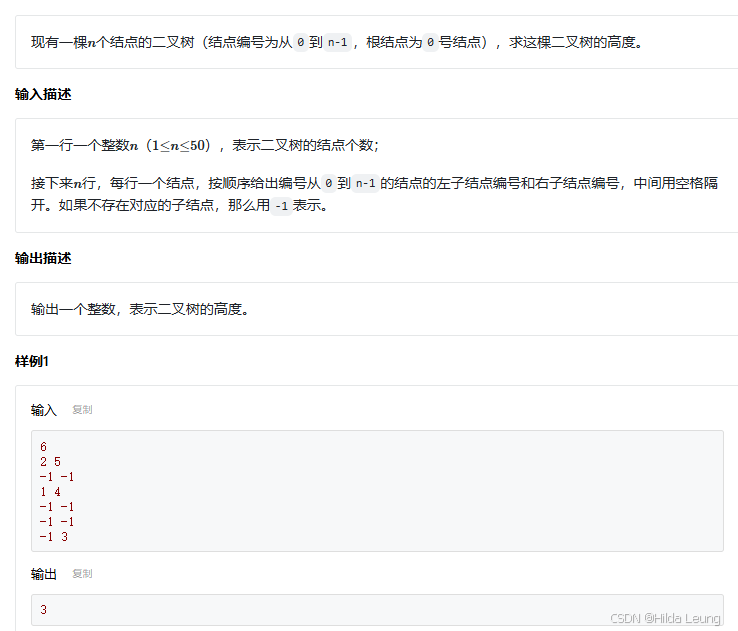
3.二叉树的高度

这道题我有3种思路：

思路一：

由二叉树层数和结点个数特性，有以下数学规律：

层数                结点个数

1                        1

2                       [2    ， 2^2）

3                       [2^2， 2^3）

......

即可以通过判断结点个数的范围求出二叉树的层数。

思路二：

这个思路灵感来自于BFS专题中关于迷宫路径步数计算问题

在这里也可以用BFS计算二叉树的“层数”。

因为上一题也是用BFS，所以就把上一题的代码略作修改，可得；

#include<cstdio>
#include<vector>
#include<queue>
using namespace std;

const int MAXN = 50;

struct Node {
	int l, r;// 左子节点和右子节点编号
}nodes[MAXN];

vector<int> layer; // 存储先序遍历结果

int getHeight(int root) {
	queue<int> q;//创建队列用于BFS
	q.push(root);//将根节点加入队列

	int height=0;
	while (!q.empty())
	{
		int cnt = q.size();

		while (cnt--)
		{
			int front = q.front();//取出队列头结点
			q.pop();
			layer.push_back(front);// 将节点编号加入层序遍历结果
			if (nodes[front].l != -1) {// 如果左子节点存在，加入队列
				q.push(nodes[front].l);
			}
			if (nodes[front].r != -1) {// 如果右子节点存在，加入队列
				q.push(nodes[front].r);
			}
		}

		height++;
	}

	return height;
}

int main()
{
	int n;
	scanf("%d", &n);

	for (int i = 0; i < n; i++)
	{
		scanf("%d%d", &nodes[i].l, &nodes[i].r);
	}

	printf("%d", getHeight(0)); // 计算并输出二叉树的高度

	
	return 0;
}

思路三：

递归求解二叉树高度

有点类似于从定义出发。首先，树的高度指树中结点的最大高度

于是答案把目标转化成，树的高度= max（根左节点Height，根右节点Height）+1

整体思路

  1. 定义高度：二叉树的高度定义为从根节点到最远叶子节点的最长路径上的节点数。
  2. 递归思想：对于每一个节点，其高度等于其左子树高度和右子树高度的最大值加1。
  3. 递归终止条件：如果当前节点为空（即节点编号为-1），则高度为0。

通过这种递归的方式，我们可以从根节点开始，逐层向下计算每个节点的高度，最终得到整棵树的高度。

代码如下：

#include <cstdio>
#include <algorithm>
using namespace std;

const int MAXN = 50;

struct Node {
    int l, r;
} nodes[MAXN];

int getHeight(int root) {
    if (root == -1) { // 如果当前节点为空，返回0
        return 0;
    }
    int leftHeight = getHeight(nodes[root].l); // 递归计算左子树高度
    int rightHeight = getHeight(nodes[root].r); // 递归计算右子树高度
    return max(leftHeight, rightHeight) + 1; // 返回左子树高度和右子树高度的最大值加1
}

int main() {
    int n;
    scanf("%d", &n); // 读取节点个数
    for (int i = 0; i < n; i++) {
        scanf("%d%d", &nodes[i].l, &nodes[i].r); // 读取每个节点的左子节点和右子节点编号
    }
    printf("%d", getHeight(0)); // 计算并输出二叉树的高度
    return 0;
}

4.二叉树结点的层号

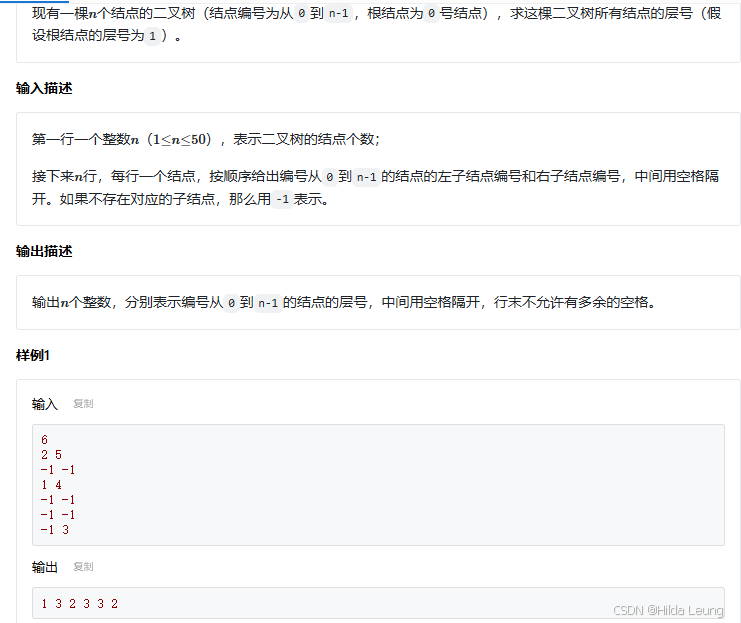
这道题可以参考BFS问题中的7.多终点迷宫问题，即按层次遍历每个结点，遍历过程中记录每个结点此时所在层次。

#include<cstdio>
#include<queue>
using namespace std;

const int MAXN = 50;

struct Node {
	int l, r;// 左子节点和右子节点编号
}nodes[MAXN];

int Height[MAXN];

void getHeight(int root) {
	queue<int> q;//创建队列用于BFS
	q.push(root);//将根节点加入队列

	int height=1;
	while (!q.empty())
	{
		int cnt = q.size();

		while (cnt--)
		{
			int front = q.front();//取出队列头结点
			q.pop();
			
			Height[front] = height;

			if (nodes[front].l != -1) {// 如果左子节点存在，加入队列
				q.push(nodes[front].l);
			}
			if (nodes[front].r != -1) {// 如果右子节点存在，加入队列
				q.push(nodes[front].r);
			}
		}
		height++;
	}

	return;
}

int main()
{
	int n;
	scanf("%d", &n);

	for (int i = 0; i < n; i++)
	{
		scanf("%d%d", &nodes[i].l, &nodes[i].r);
	}

	getHeight(0);
	
	for (int i = 0; i < n; i++)
	{
		printf("%d", Height[i]);
		if (i < n - 1)
			printf(" ");
	}

	return 0;
}

5.翻转二叉树

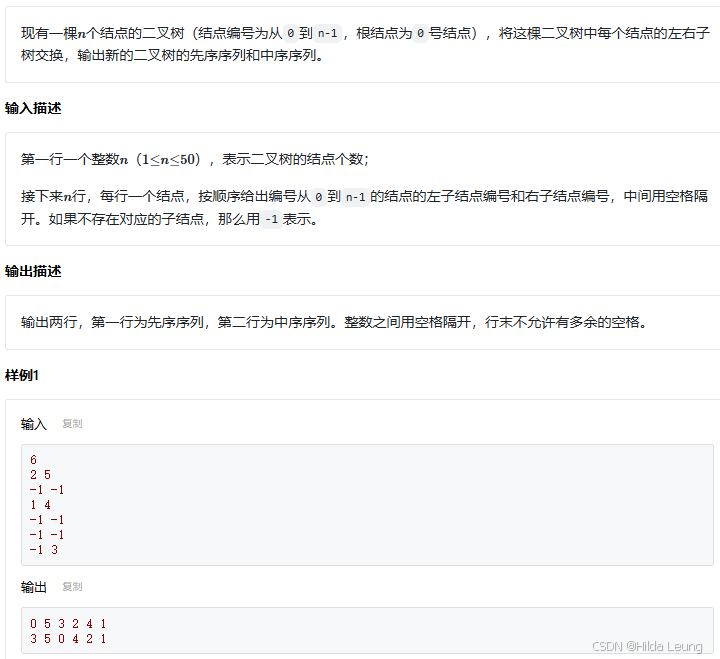
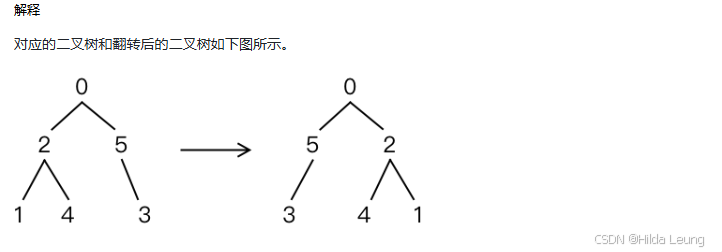
思路：递归交换与遍历

我们需要将每个节点的左右子树交换，

然后输出交换后的二叉树的先序序列和中序序列，这里我们已经在 问题1 实现了

这个问题可以通过递归的方法来解决，主要分为以下几个步骤：

  1. 递归交换左右子树：首先，我们需要遍历整棵树，对每个节点进行左右子树的交换。这个过程可以通过递归实现，从根节点开始，依次对每个节点的左右子树进行交换。

  2. 遍历二叉树：在交换完所有节点的左右子树之后，我们需要对新的二叉树进行遍历，以获取先序序列和中序序列。先序遍历和中序遍历也是通过递归实现的。

  3. 输出结果：最后，我们将遍历得到的结果输出。

我知道要用递归，但是递归设计起来真的让我感到有点吃力：

#include<cstdio>
#include<vector>
#include <algorithm>
using namespace std;

const int MAXN = 50;

struct Node {
	int l, r;// 左子节点和右子节点编号
}nodes[MAXN];

vector<int> pre,in,post; // 存储先序遍历结果

void preOrder(int root) 
{
	if (root == -1) 
    {
		return;
	}
	pre.push_back(root); // 先序遍历：根节点 -> 左子树 -> 右子树
	preOrder(nodes[root].l);
	preOrder(nodes[root].r);
}

void inOrder(int root) 
{
	if (root == -1) 
    {
		return;
	}
	inOrder(nodes[root].l);
	in.push_back(root); // 中序遍历：左子树 -> 根节点 -> 右子树
	inOrder(nodes[root].r);
}

void revert(int root) 
{
	if (root == -1) {
		return;
	}
	revert(nodes[root].l); // 递归交换左子树
	revert(nodes[root].r); // 递归交换右子树
	swap(nodes[root].l, nodes[root].r); // 交换当前节点的左右子树
}

int main()
{
    int n;
    scanf("%d", &n);
    for (int i = 0; i < n; i++) 
    {
        scanf("%d%d", &nodes[i].l, &nodes[i].r);
    }

    revert(0); // 从根节点开始递归交换左右子树
    
    preOrder(0); // 从根节点开始先序遍历
    inOrder(0); // 从根节点开始中序遍历
    
    for (int i = 0; i < (int)pre.size(); i++) 
    {
        printf("%d", pre[i]);
        if (i < (int)pre.size() - 1) 
        {
            printf(" ");
        }
    }
    printf("\n");
    
    for (int i = 0; i < (int)in.size(); i++) 
    {
        printf("%d", in[i]);
        if (i < (int)in.size() - 1) 
        {
            printf(" ");
        }
    }

	return 0;
}

核心代码：

void revert(int root) 
{
    if (root == -1) {
        return;
    }
    revert(nodes[root].l); // 递归交换左子树
    revert(nodes[root].r); // 递归交换右子树
    //当某个结点height=2时，此时左右子树return均为空，此时可以交换左右结点
    //以此类推
    swap(nodes[root].l, nodes[root].r); // 交换当前节点的左右子树
}

 6.先序中序还原二叉树

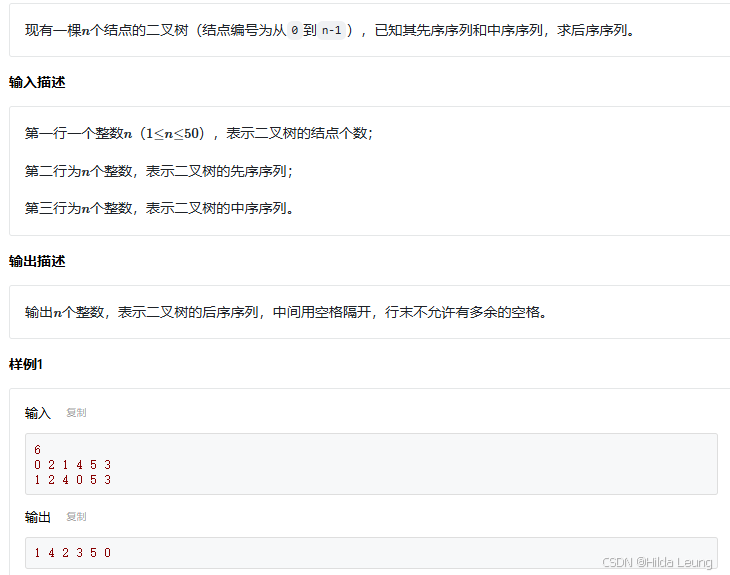
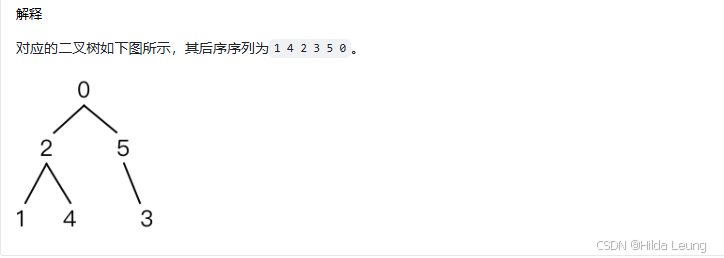
还是递归

整体思路

  1. 确定根节点：先序遍历的第一个元素就是二叉树的根节点。
  2. 分割中序遍历：在中序遍历中找到根节点的位置，根节点左侧的元素属于左子树，右侧的元素属于右子树。
  3. 递归构建子树：根据中序遍历的分割结果，在先序遍历中找到对应的左子树和右子树的部分，递归地构建左子树和右子树。
  4. 后序遍历：在构建完整个二叉树后，对其进行后序遍历，得到后序序列。

具体过程细节

  1. 构建二叉树：

    • 从先序遍历中取出第一个元素作为根节点。
    • 在中序遍历中找到这个根节点的位置，分割出左子树和右子树的中序遍历序列。
    • 根据左子树和右子树的中序遍历序列的长度，在先序遍历中分割出对应的左子树和右子树的先序遍历序列。
    • 递归地对左子树和右子树进行上述操作，直到构建出完整的二叉树。

时空复杂度

  • 时间复杂度：每次递归都需要在中序遍历中查找根节点的位置，时间复杂度为O(n)，总共需要进行n次递归，因此总时间复杂度为O(n2)。在最坏情况下（例如树是一个链表），查找根节点的位置需要遍历整个中序遍历序列。
  • 空间复杂度：递归栈的深度最多为n，因此空间复杂度为O(n)。

代码如下：

#include<cstdio>
#include<vector>
using namespace std;

const int MAXN = 50;

struct Node 
{
	int l, r;
}nodes[MAXN];

vector<int> pre, in, post;

//preL 和 preR：先序遍历序列的左端点和右端点索引，表示当前子树在先序遍历中的范围。
//inL 和 inR：中序遍历序列的左端点和右端点索引，表示当前子树在中序遍历中的范围。
int buildTree(int preL, int preR, int inL, int inR) 
{
    if (preL > preR) //如果当前子树的先序遍历范围是无效的（即 preL 大于 preR），说明没有节点需要处理
    {
        return -1;//返回 -1 表示空树。
    }
    
    int root = pre[preL];//先序遍历的第一个元素 pre[preL] 是当前子树的根节点，记作 root

    //查找根节点在中序遍历中的位置
    int inIndexOfRoot;
    for (int i = inL; i <= inR; i++) 
    {
        if (in[i] == root) 
        {
            inIndexOfRoot = i;
            break;
        }
    }
    
    int leftCount = inIndexOfRoot - inL;//计算左子树的节点数

    //递归构建左子树
    nodes[root].l = buildTree(preL + 1, preL + leftCount, inL, inIndexOfRoot - 1);
    
    //递归构建右子树
    nodes[root].r = buildTree(preL + leftCount + 1, preR, inIndexOfRoot + 1, inR);

    return root;
}

void postOrder(int root) 
{
    if (root == -1) 
    {
        return;
    }
    postOrder(nodes[root].l);
    postOrder(nodes[root].r);
    post.push_back(root);
}

int main() 
{
    int n, x;
    scanf("%d", &n);
    
    for (int i = 0; i < n; i++) 
    {
        scanf("%d", &x);
        pre.push_back(x);
    }
    
    for (int i = 0; i < n; i++) 
    {
        scanf("%d", &x);
        in.push_back(x);
    }

    int root = buildTree(0, n - 1, 0, n - 1);

    postOrder(root);
    
    for (int i = 0; i < (int)post.size(); i++) 
    {
        printf("%d", post[i]);
        if (i < (int)post.size() - 1) 
        {
            printf(" ");
        }
    }
    return 0;
}

核心代码：

//preL 和 preR：先序遍历序列的左端点和右端点索引，表示当前子树在先序遍历中的范围。
//inL 和 inR：中序遍历序列的左端点和右端点索引，表示当前子树在中序遍历中的范围。
int buildTree(int preL, int preR, int inL, int inR) 
{
    if (preL > preR) //如果当前子树的先序遍历范围是无效的（即 preL 大于 preR），说明没有节点需要处理
    {
        return -1;//返回 -1 表示空树。
    }
    
    int root = pre[preL];//先序遍历的第一个元素 pre[preL] 是当前子树的根节点，记作 root

 //查找根节点在中序遍历中的位置
    int inIndexOfRoot;
    for (int i = inL; i <= inR; i++) 
    {
        if (in[i] == root) 
        {
            inIndexOfRoot = i;
            break;
        }
    }
    
    int leftCount = inIndexOfRoot - inL;//计算左子树的节点数

//递归构建左子树
    nodes[root].l = buildTree(preL + 1, preL + leftCount, inL, inIndexOfRoot - 1);
    
//递归构建右子树
    nodes[root].r = buildTree(preL + leftCount + 1, preR, inIndexOfRoot + 1, inR);

    return root;
}

这部分代码可以画图递归理解一下。 

 7.后序中序还原二叉树

如果理解了6.先序中序还原二叉树，这道题修改便变得简单很多了

#include<cstdio>
#include<vector>
using namespace std;

const int MAXN = 50;

struct Node 
{
	int l, r;
}nodes[MAXN];

vector<int> pre, in, post;

//preL 和 preR：先序遍历序列的左端点和右端点索引，表示当前子树在先序遍历中的范围。
//inL 和 inR：中序遍历序列的左端点和右端点索引，表示当前子树在中序遍历中的范围。
int buildTree(int postL, int postR, int inL, int inR) 
{
    if (postL > postR) //如果当前子树的先序遍历范围是无效的（即 preL 大于 preR），说明没有节点需要处理
    {
        return -1;//返回 -1 表示空树。
    }
    
    int root = post[postR];//先序遍历的第一个元素 pre[preL] 是当前子树的根节点，记作 root

    //查找根节点在中序遍历中的位置
    int inIndexOfRoot;
    for (int i = inL; i <= inR; i++) 
    {
        if (in[i] == root) 
        {
            inIndexOfRoot = i;
            break;
        }
    }
    
    int leftCount = inIndexOfRoot - inL;//计算左子树的节点数

    //递归构建左子树
    nodes[root].l = buildTree(postL, postL + leftCount-1, inL, inIndexOfRoot - 1);
    
    //递归构建右子树
    nodes[root].r = buildTree(postL + leftCount , postR-1, inIndexOfRoot + 1, inR);

    return root;
}

void preOrder(int root) 
{
    if (root == -1) 
    {
        return;
    }

    pre.push_back(root);
    preOrder(nodes[root].l);
    preOrder(nodes[root].r);
}

int main() 
{
    int n, x;
    scanf("%d", &n);
    
    for (int i = 0; i < n; i++) 
    {
        scanf("%d", &x);
        post.push_back(x);
    }
    
    for (int i = 0; i < n; i++) 
    {
        scanf("%d", &x);
        in.push_back(x);
    }

    int root = buildTree(0, n - 1, 0, n - 1);

    preOrder(root);
    
    for (int i = 0; i < (int)pre.size(); i++) 
    {
        printf("%d", pre[i]);
        if (i < (int)pre.size() - 1) 
        {
            printf(" ");
        }
    }
    return 0;
}

先序和后序不能确定一棵二叉树，如下图：

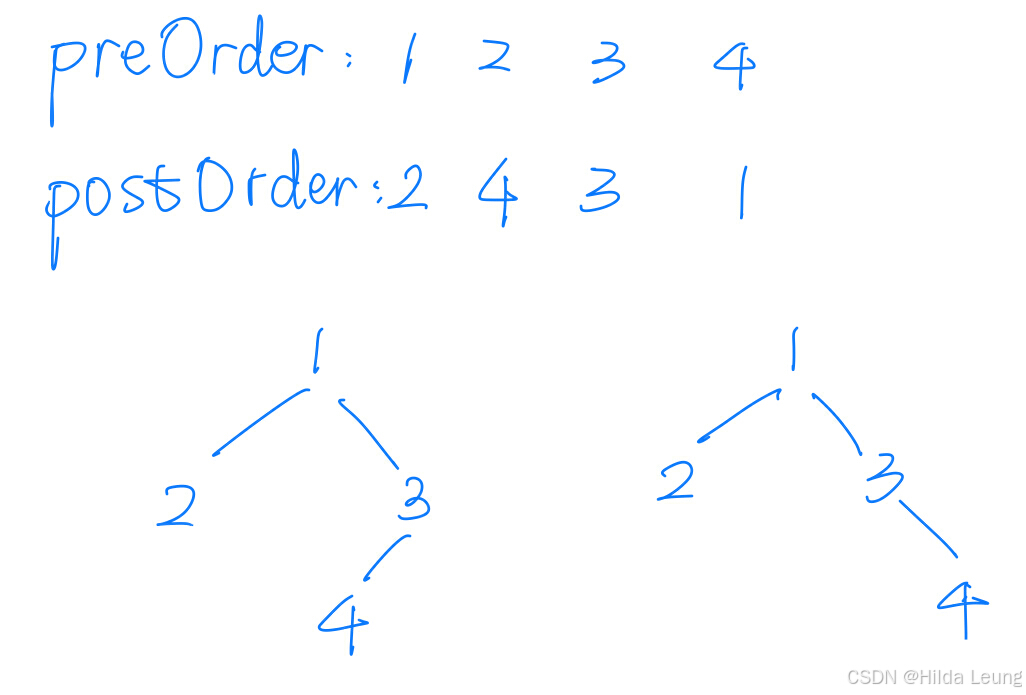
8.层序中序还原二叉树

时空复杂度

  • 时间复杂度：O(n^2)，其中n是节点数。在最坏情况下，每次递归都需要遍历中序序列来找到根节点的位置。
  • 空间复杂度：O(n)，主要用于存储节点信息和递归调用栈。

这道题结合 Q6 ＆ Q7 可以解决

代码如下：

#define _CRT_SECURE_NO_WARNINGS
#include <cstdio>
#include <map>
#include <vector>
using namespace std;

const int MAXN = 50;

struct Node {
    int l, r;
} nodes[MAXN];

vector<int> pre, in, layer;

int buildTree(vector<int> layer, int inL, int inR) 
{
    if (layer.empty())
    {
        return -1;
    }

    int root = layer[0];
    map<int, bool> isLeft;
    int inIndexOfRoot;
    for (int i = inL; i <= inR; i++)
    {
        if (in[i] == root) 
        {
            inIndexOfRoot = i;
            break;
        }
        //找到inIndexOfRoot前对层序数列标注true
        else
        {
            isLeft[in[i]] = true;
        }
    }

    vector<int> leftLayer, rightLayer;

    for (int i = 1; i < layer.size(); i++)
    {
        if (isLeft[layer[i]])
        {
            leftLayer.push_back(layer[i]);
        }

        else
        {
            rightLayer.push_back(layer[i]);
        }
    }

    nodes[root].l = buildTree(leftLayer, inL, inIndexOfRoot - 1);
    nodes[root].r = buildTree(rightLayer, inIndexOfRoot + 1, inR);
    return root;
}

void preOrder(int root) {
    if (root == -1) 
    {
        return;
    }

    pre.push_back(root);
    preOrder(nodes[root].l);
    preOrder(nodes[root].r);
}

int main()
{
    int n, x;
    scanf("%d", &n);

    for (int i = 0; i < n; i++)
    {
        scanf("%d", &x);
        layer.push_back(x);
    }

    for (int i = 0; i < n; i++)
    {
        scanf("%d", &x);
        in.push_back(x);
    }

    int root = buildTree(layer, 0, n - 1);

    preOrder(root);

    for (int i = 0; i < (int)pre.size(); i++) {
        printf("%d", pre[i]);
        if (i < (int)pre.size() - 1) {
            printf(" ");
        }
    }

    return 0;
}

9.二叉树的最近公共祖先

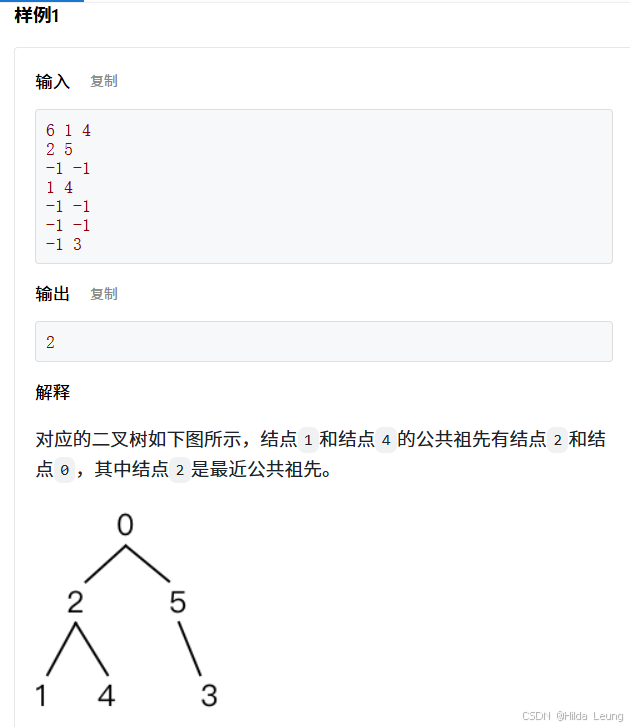
上面是我为了理解递归代码画出来的，如果不太清晰大家可以自己画一下。 

代码如下：
 

#define _CRT_SECURE_NO_WARNINGS
#include <cstdio>
#include <vector>
using namespace std;

const int MAXN = 50;

struct Node 
{
    int l, r;
} nodes[MAXN];

int LCA(int root, int p, int q) 
{

    if (root == -1) 
    { 
        // 递归终止条件：当前节点为空
        return -1;
    }
    
    if (root == p || root == q) 
    { 
        // 找到目标节点之一
        return root;
    }
    
    int leftResult = LCA(nodes[root].l, p, q); // 在左子树中查找
    int rightResult = LCA(nodes[root].r, p, q); // 在右子树中查找
    
    if (leftResult != -1 && rightResult != -1) 
    { 
        // 左子树和右子树都找到了目标节点
        return root; // 当前节点是最近公共祖先
    }
    
    else if (leftResult != -1) 
    { 
        // 只在左子树中找到目标节点
        return leftResult;
    }
    
    else 
    { 
        // 只在右子树中找到目标节点
        return rightResult;
    }
}

int main()
{
    int n, p, q;
    scanf("%d%d%d", &n,&p,&q);
    
    for (int i = 0; i < n; i++)
    {
        scanf("%d%d", &nodes[i].l, &nodes[i].r);
    }

    printf("%d", LCA(0, p, q));
    return 0;
}

 10.二叉树路径和

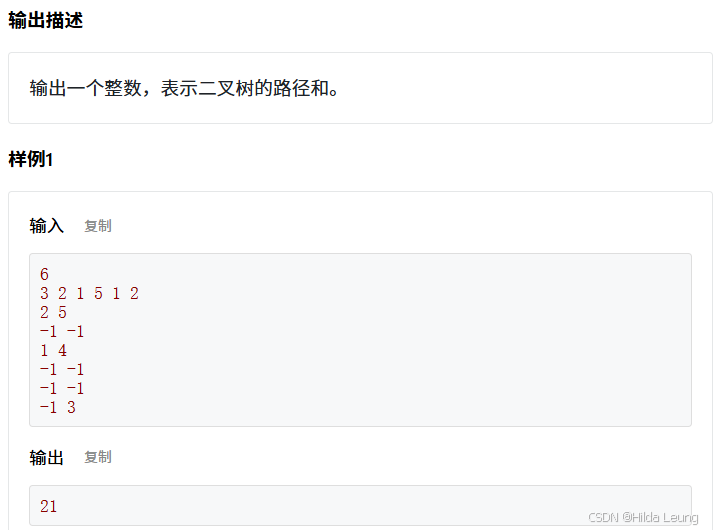
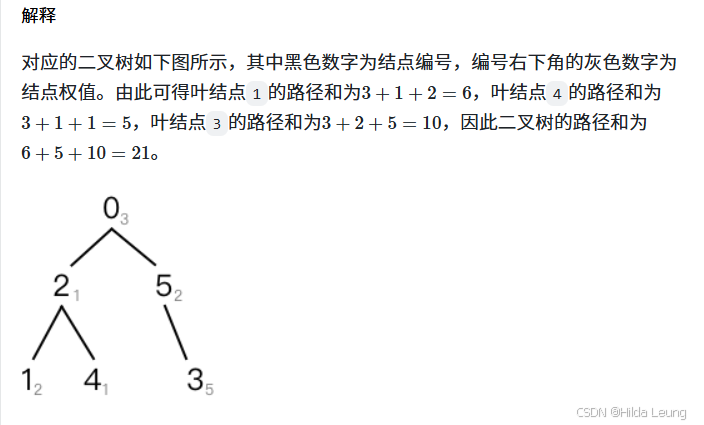
通过深度优先搜索（DFS）来遍历整棵树，并在遍历过程中累加每个叶结点的路径和。

代码如下：

#define _CRT_SECURE_NO_WARNINGS
#include <cstdio>
#include <vector>
using namespace std;

const int MAXN = 50;

struct Node 
{
    int data;
    int l, r;
} nodes[MAXN];

int treePathSum = 0;
void getTreePathSum(int root, int nodePathSum)
{
    if (root == -1) return; // 如果当前结点不存在，直接返回

    nodePathSum += nodes[root].data;// 累加当前结点的权值到路径和

    if (nodes[root].l == -1 && nodes[root].r == -1) // 如果当前结点是叶结点
    {
        treePathSum += nodePathSum; // 累加路径和到总路径和
    }
    else
    {
        getTreePathSum(nodes[root].l, nodePathSum);//递归遍历左子结点
        getTreePathSum(nodes[root].r, nodePathSum);//递归遍历右子结点
    }
}

int main()
{
    int n;
    scanf("%d", &n);

    for (int i = 0; i < n; i++)
    {
        scanf("%d", &nodes[i].data);
    }

    for (int i = 0; i < n; i++)
    {
        scanf("%d%d", &nodes[i].l, &nodes[i].r);
    }

    getTreePathSum(0, 0);//从根节点开始计算路径和
    printf("%d", treePathSum);
    return 0;

}

11.二叉树的带权路径长度

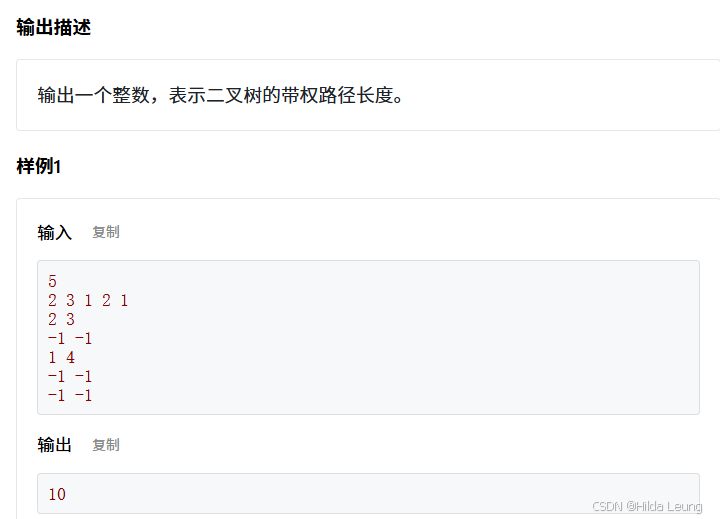
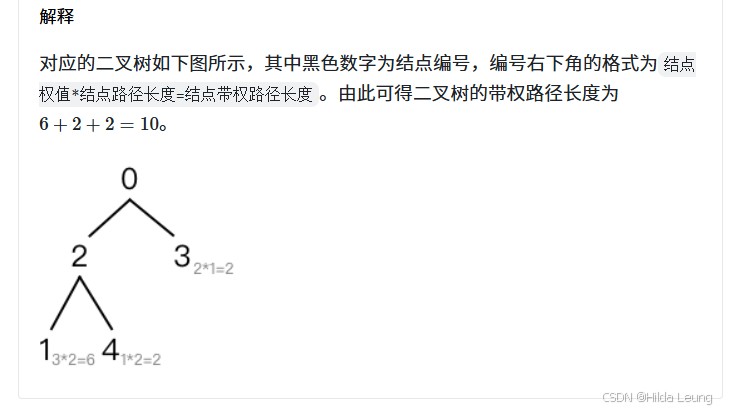
依旧是DFS的思想，只是在递归的过程中注意计算深度

代码如下：

#define _CRT_SECURE_NO_WARNINGS
#include <cstdio>
#include <vector>
using namespace std;

const int MAXN = 50;

struct Node 
{
    int data;
    int l, r;
} nodes[MAXN];

int treeWeightedPathLength = 0;

//DFS函数，计算带权路径长度
void getTreeWeightedPathLength(int root, int nodePathLength) 
{
    if (root == -1)return;//如果结点不存在，返回

    if (nodes[root].l == -1 && nodes[root].r == -1)// 如果是叶节点
    {
        treeWeightedPathLength += nodes[root].data * nodePathLength;//计算带权路径长度并累加
    }
    else
    {
        nodePathLength++;//路径长度加一
        getTreeWeightedPathLength(nodes[root].l, nodePathLength);//递归访问左子结点
        getTreeWeightedPathLength(nodes[root].r, nodePathLength);//递归访问右子结点
    }

}


int main()
{
    int n;
    scanf("%d", &n);

    for (int i = 0; i < n; i++)
    {
        scanf("%d", &nodes[i].data);//读取每个结点的权值
    }

    for (int i = 0; i < n; i++)
    {
        scanf("%d%d", &nodes[i].l, &nodes[i].r);
    }

    getTreeWeightedPathLength(0, 0);//从根节点开始计算带权路径长度
    printf("%d", treeWeightedPathLength);//输出结果

    return 0;

}

12.二叉树的左视图序列

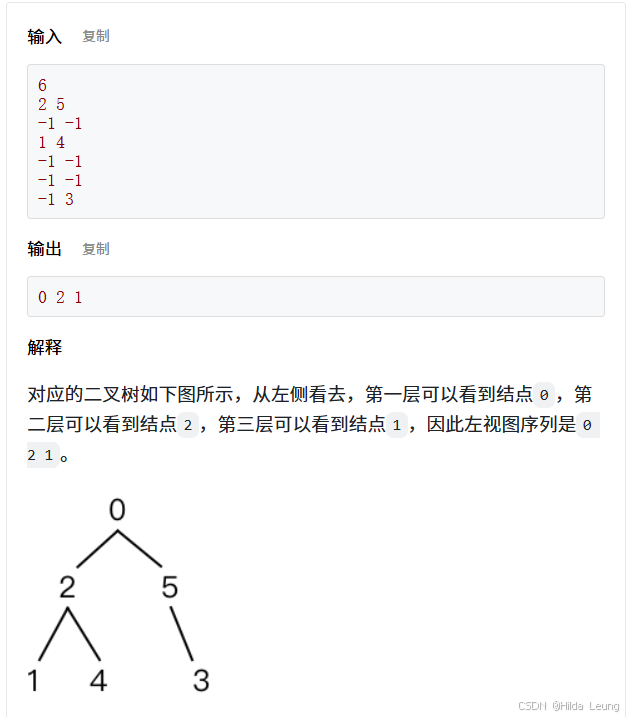
使用广度优先搜索（BFS）来解决这个问题。BFS能够逐层遍历二叉树，从而方便地找到每层的最左边结点

#define _CRT_SECURE_NO_WARNINGS
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;

const int MAXN = 50;

struct Node 
{
    int data;
    int l, r;
} nodes[MAXN];

vector<int> getLeftViewSeq(int root)
{
    vector<int> leftViewSeq;
    queue<int> q;
    q.push(root);//初始化队列，加入根节点
    while (!q.empty())
    {
        int cnt = q.size();//当前层的结点数

        for (int i = 0; i < cnt; i++)
        {
            int front = q.front();
            q.pop();

            if (i == 0)
                leftViewSeq.push_back(front);//记录每层的最左边结点

            if (nodes[front].l != -1)
                q.push(nodes[front].l);//加入左子结点

            if (nodes[front].r != -1)
                q.push(nodes[front].r);//加入右子结点
        }
    }

    return leftViewSeq;
}

int main()
{
    int n;
    scanf("%d", &n);

    for (int i = 0; i < n; i++)
    {
        scanf("%d%d", &nodes[i].l, &nodes[i].r);
    }
    vector<int> leftViewSeq = getLeftViewSeq(0);

    for (int i = 0; i < (int)leftViewSeq.size(); i++)
    {
        printf("%d", leftViewSeq[i]);
        if (i < (int)leftViewSeq.size() - 1)
            printf(" ");
    }
}

13.满二叉树的判定

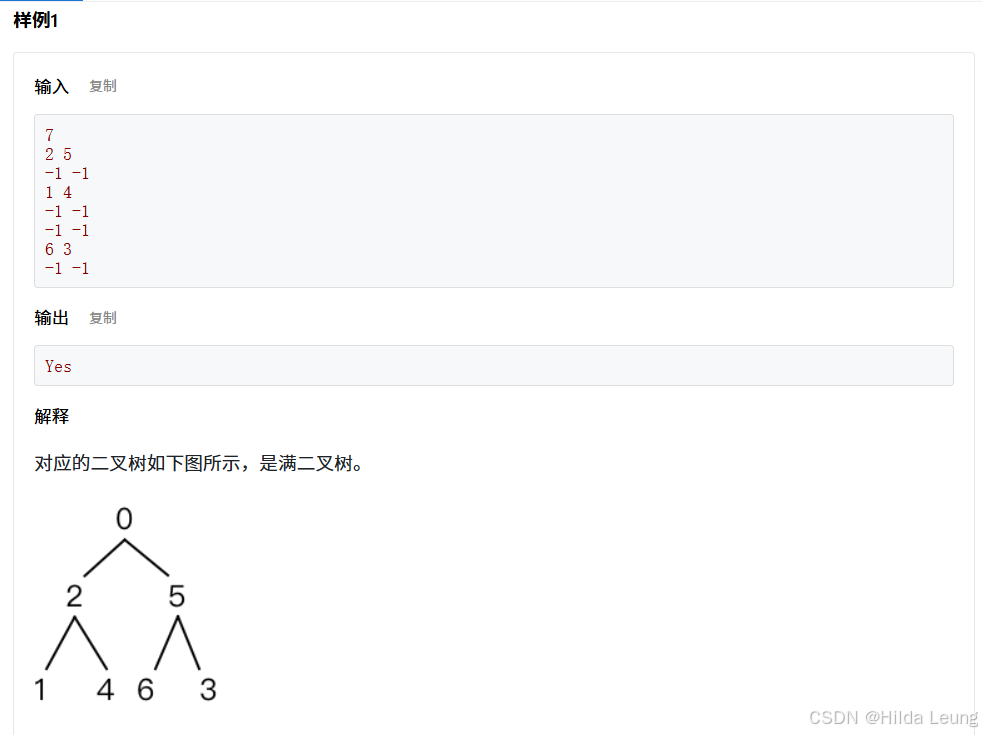
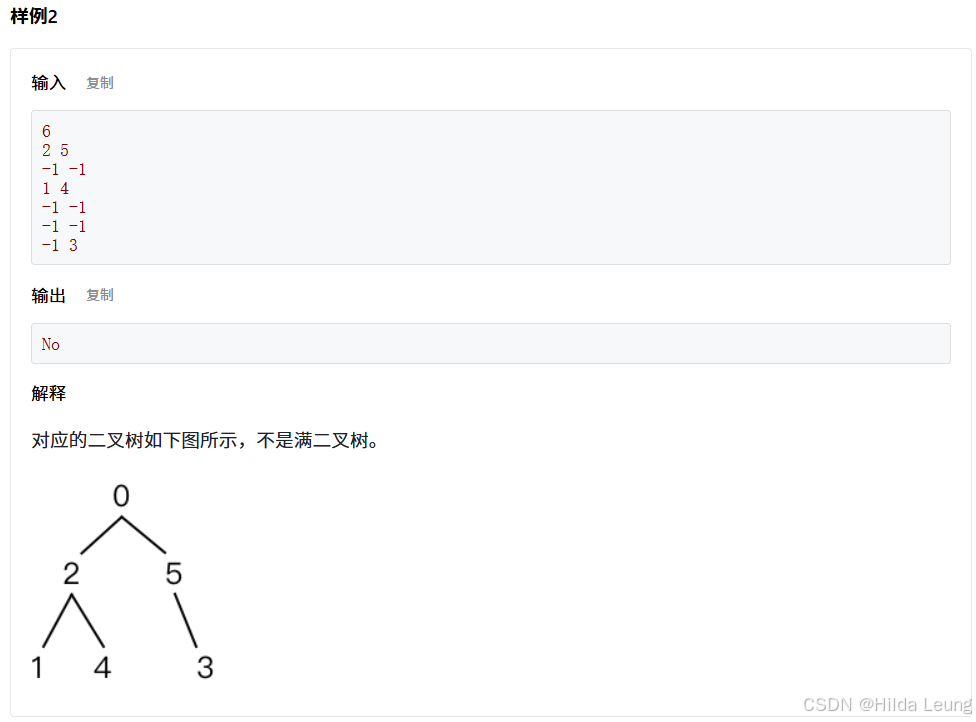
利用满二叉树的定义，即每一层的结点数都达到了当层能达到的最大结点数。具体来说，如果二叉树的层数为k，且结点总数为2^k−1，那么这棵二叉树就是满二叉树。我们可以通过递归的方法来判断每个子树是否满足这个条件。 

满二叉树的定义

  1. 每个非叶子节点都有两个子节点。
  2. 所有叶子节点都在同一层。
#include<cstdio>
#include<utility>
using namespace std;

typedef pair<int, bool> TreeInfo;

const int MAXN = 64;

struct Node 
{
	int l, r;
}nodes[MAXN];

int isFullBinaryTree(int root)
{
	if (root == -1)//如果当前结点为空，返回0 
	{
		return 0;
	}

	int leftNodeCount = isFullBinaryTree(nodes[root].l);//递归计算左子树结点总数
	int rightNodeCount = isFullBinaryTree(nodes[root].r);//递归计算右子树结点总数
	
	if (leftNodeCount == rightNodeCount)//如果左子树和右子树结点总数相等
	{
		return leftNodeCount + rightNodeCount + 1;// 返回总数+1
	}

	else
	{
		return -1; // 否则返回-1，表示不是满二叉树
	}
}

int main()
{
	int n;
	scanf("%d", &n);//读取结点个数

	for (int i = 0; i < n; i++)
	{
		scanf("%d%d", &nodes[i].l, &nodes[i].r);
	}

	printf(isFullBinaryTree(0) != -1 ? "Yes" : "No");
	return 0;
}

14.完全二叉树的判定

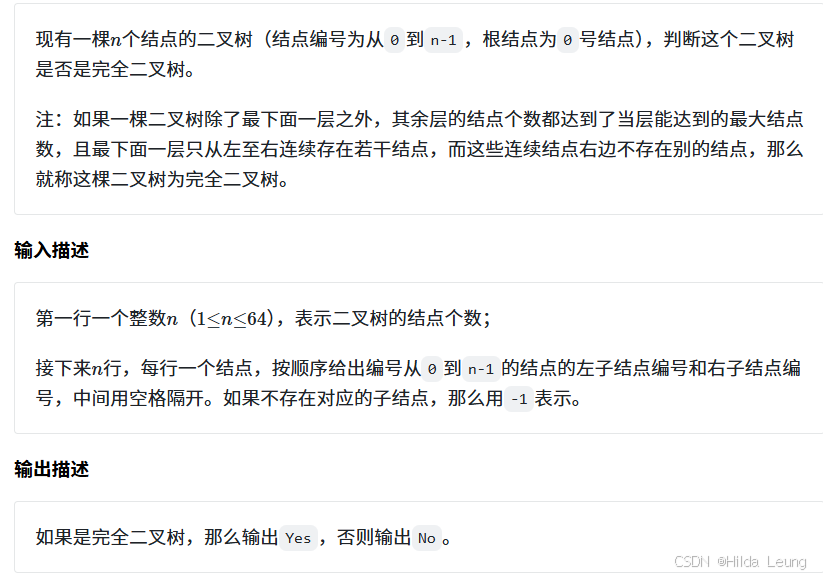
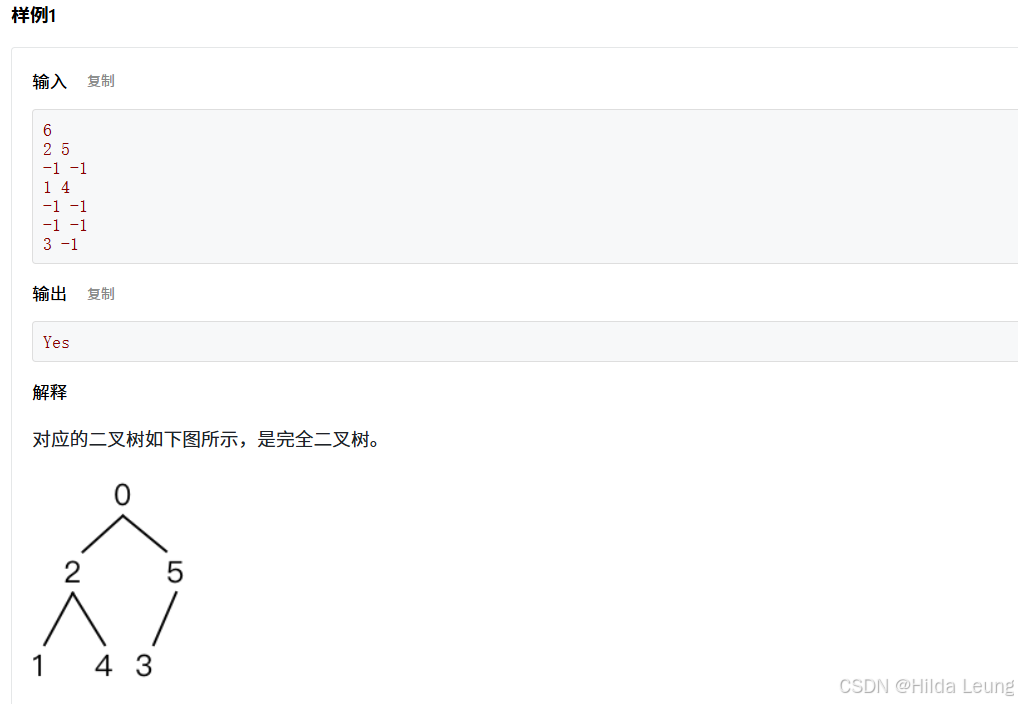
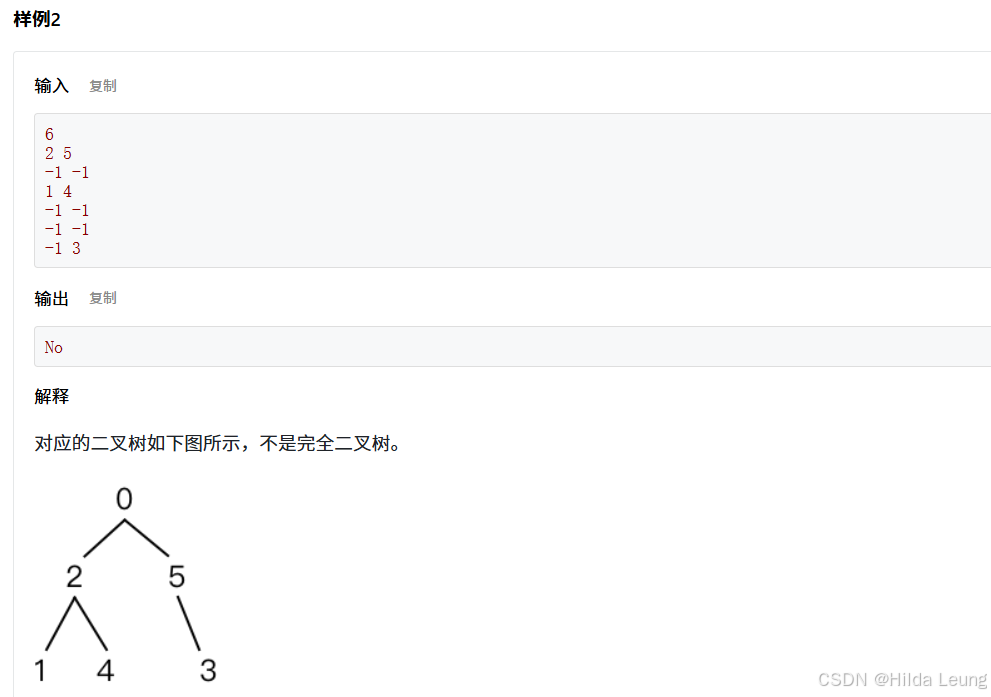
利用广度优先搜索（BFS）的特性。

BFS能够逐层遍历树的节点，这有助于我们检查每一层的节点是否满足完全二叉树的条件。

具体来说，我们需要确保在遇到第一个没有子节点的节点后，后续的所有节点都应该是叶子节点，且不存在任何非叶子节点。

代码如下：

#define _CRT_SECURE_NO_WARNINGS
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;

const int MAXN = 64;

struct Node 
{
    int l, r;

} nodes[MAXN];

bool isCompleteBinaryTree(int root) 
{
    queue<int> q;
    q.push(root);
    bool gotNullNode = false;

    while (!q.empty()) 
    {
        int front = q.front();
        q.pop();

        if (front == -1) 
        {
            gotNullNode = true;
        }

        else 
        {
            if (gotNullNode) 
            {
                return false;
            }

            q.push(nodes[front].l);
            q.push(nodes[front].r);
        }
    }
    return true;
}

int main() 
{
    int n;
    scanf("%d", &n);

    for (int i = 0; i < n; i++) 
    {
        scanf("%d%d", &nodes[i].l, &nodes[i].r);
    }
    
    printf(isCompleteBinaryTree(0) ? "Yes" : "No");
    
    return 0;
}

遍历二叉树
weixin_52555350的博客
03-25 5393
二叉树遍历
二叉树遍历
qq_55078860的博客
07-07 1177
例如，“DBACEGF ABCDEFG”，通过先序遍历知道根节点为D，根据中序遍历可知，左子树中序遍历为ABC，右子树中序遍历为EFG，然后通过先序遍历得到左右子树的先序遍历（BAC、EGF）和根节点D的左右节点（B、E），继续对左右子树（“BAC ABC”、“EGF EFG”）进行上述操作，直至结束。基于先序序列和中序序列的节点数目相同，得到k-il=x-pl，所以x=k-il+pl，那么左子树先序序列[pl+1,k-il+pl]；注意：访问根，先序遍历左子树，左子树为空或已遍历才可以遍历右子树。
数据结构——树（二叉树的遍历）
最新发布
weixin_73165588的博客
05-20 417
（1）DLR：先（根）序遍历、LDR：中（根）序遍历、LRD：后（根）序遍历（2）层次遍历：逐层遍历。
二叉树遍历（前序、中序、后序、层次遍历、深度优先、广度优先）
热门推荐
My_Jobs的专栏
02-03 43万+
二叉树是一种非常重要的数据结构，很多其它数据结构都是基于二叉树的基础演变而来的。对于二叉树，有深度遍历和广度遍历，深度遍历有前序、中序以及后序三种遍历方法，广度遍历即我们平常所说的层次遍历。因为树的定义本身就是递归定义，因此采用递归的方法去实现树的三种遍历不仅容易理解而且代码很简洁，而对于广度遍历来说，需要其他数据结构的支撑，比如堆了。所以，对于一段代码来说，可读性有时候要比代码本身的效率要重要的
易语言二叉树遍历
07-21
二叉树遍历是理解数据结构和算法的基础，它包括前序遍历、中序遍历和后序遍历三种主要方法。 1. **二叉树的基本概念**： - 二叉树是一种特殊的树结构，每个节点最多有两个子节点，通常称为左子节点和右子节点。 -...
【C语言二叉树遍历实例】C语言二叉树遍历实例
05-20
二叉树的遍历C语言二叉树遍历实例C语言二叉树遍历实例C语言二叉树遍历实例C语言二叉树遍历实例C语言二叉树遍历实例C语言二叉树遍历实例C语言二叉树遍历实例C语言二叉树遍历实例C语言二叉树遍历实例C语言二叉树遍历...
二叉树遍历流程图（先序、中序、后序、宽度遍历）
05-01
二叉树遍历是计算机科学中处理树结构数据时常用的一种技术，主要分为四种类型：先序遍历、中序遍历、后序遍历和宽度优先遍历。这些遍历方法各有特点，适用于不同的场景。 1. **先序遍历**： - **递归实现**：先...
二叉树遍历问题-二叉树遍历问题
11-12
二叉树遍历是计算机科学中的一个重要概念，主要应用于数据结构和算法领域。二叉树是一种特殊的树形数据结构，每个节点最多有两个子节点，通常称为左子节点和右子节点。二叉树遍历是指按照特定顺序访问二叉树的所有...
二叉树遍历问题 关于二叉树遍历问题的一些总结
07-05
二叉树遍历是计算机科学中处理树结构数据时常用的一种技术，对于理解和解决与树相关的算法问题至关重要。本文将深入探讨二叉树的三种遍历方法：先序遍历、中序遍历和后序遍历，并提供相关算法模板。 1. **先序遍历*...
数据结构--二叉树遍历(详细过程)
m0_56283131的博客
04-21 4万+
详细到啰嗦的程度，完全0基础都可完成。
二叉树的五种遍历方式
weixin_47382783的博客
03-29 1万+
目录 1、前序遍历 （1）递归实现前序遍历 （2）非递归实现前序遍历 2、中序遍历 （1）递归实现中序遍历 （2）非递归实现中序遍历 3、后序遍历 （1）递归实现后序遍历 （2）非递归实现后序遍历 4、层序遍历 二叉树是一种重要的数据结构，其遍历方式分为：深度遍历和广度遍历，深度遍历有前序、中序以及后序三种遍历方法，广度遍历即就是层次遍历。如下图： class TreeNode{ int val; TreeNode left; TreeNode ..
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值