LeetCode算法题之64. Minimum Path Sum（Medium）【Python3题解】

题目描述：
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

Example:

Input:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.

题目大意：

• 给你一个m x n 的非负数组，你在左上角，目标在右下角，你每次只能选择向右或者向下走动，问你，当你走到右下角目标时，走过的路径中，路径中包含的数的加和最小值为多少？
• 也就是哪一条路径可以使得这条路径的数的加和最小

解题思路：

• 首先声明，这道题是在动态规划的标签下的一道题目，基本动态规划解法，就是最优解
• 因为本人做题顺序的原因，在看到这道题的时候，自然而然就会想到之前做过的一道题，LeetCode算法题之62. Unique Paths（medium）【Python3题解】
  如果超链接这道题不知道的朋友可以去看看，看过之后，对这道题可能会有新的理解，其实是异曲同工之妙
• 开始说这道题的想法，既然是动态规划解法，那首先dp数组的定义，就需要明确，要不然你下面没法推导
• 本人这样定义：dp[i][j]代表你到达第i行第j列的位置时，数值加和的最小值
• 那么和超链接的那道题一样，下面上一张图，一图胜过千言万语
  
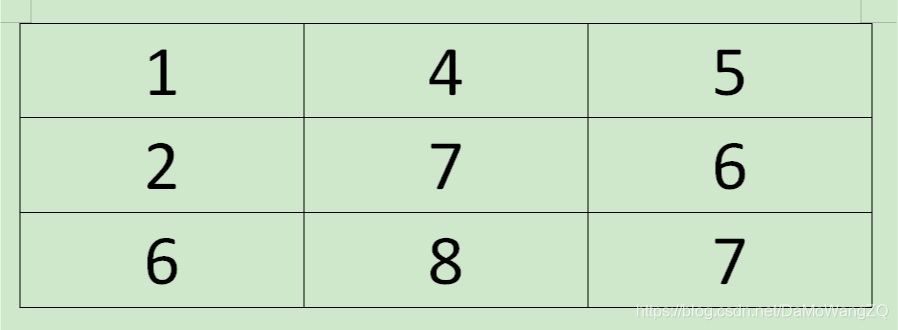
• 这一堆数是啥意思？这就是我们要填充完整的dp table，所谓动态规划，你把这张表，填完了，基本答案就在表里了
• 这表里的每个位置的数字就是到达该位置的路径，经过的数的最小值
• 怎么算的？
• 首先，看第0行，第0列，那不就是题目给你的数组的[0][0]号位置的数值吗，因为你要计算数的最小值啊，定要一个数一个数加到一起啊
• 接下来，再看第0行，第1列，怎么得来的？你走到第0行，第1列，就一种选择啊，就是向右走啊，所以就是给定数组的[0][1]号元素加上它前一个元素的数值，就是表中的数
• 那第0行的所有数，就都可以推出来了
• 再看列，为什么是这个顺序？因为你在做完超链接那道题之后，你自然会这么做
• 有了上面行的解法，下面列，还不是一样，你也就一种选择啊，就是向下走，那就加呗
• 等你把表的第0行和第0列都填充好了，那所谓的base case你就完成了
• 下面开始，递推
• 先看第1行第1列那个7，怎么来的？因为你到那个位置还不是就有两种选择，要么你从上面来，要么你从左面来，你现在上面左面都是最小路径数值的和，那到这最小值，咋算？就是给定数组的那个位置的数，加上上面或者左面那个位置的dp表中的数，看哪个小，取哪个，填充
• 你这个7也有了，那么它旁边的6，不也有了，这些有了，最下面的那一行，还是一样，按照前面的公式推就完了
• 等把dp table 都推完了，最后返回dp[-1][-1],不就是答案吗
• 结束！

少废话，上代码：

class Solution:
    def minPathSum(self, grid):
        row, column = len(grid), len(grid[0])
        dp = [[grid[0][0] for i in range(column)] for j in range(row)]

        # 开始填充第一行
        for i in range(1, column):
            dp[0][i] = grid[0][i] + dp[0][i-1]
        # 开始填充第一列
        for i in range(1, row):
            dp[i][0] = grid[i][0] + dp[i-1][0]
        # 前期准备工作已做好，开始向下填充dp table
        for i in range(1, row):
            for j in range(1, column):
                dp[i][j] = min(grid[i][j]+dp[i][j-1], grid[i][j]+dp[i-1][j])

        return dp[-1][-1]

运行时间和内存占用：

• Runtime: 96 ms, faster than 91.99% of Python3 online submissions for Minimum Path Sum.
• Memory Usage: 15.1 MB, less than 26.32% of Python3 online submissions for Minimum Path Sum.