c++算法四

1.BFS算法解决FloodFill算法

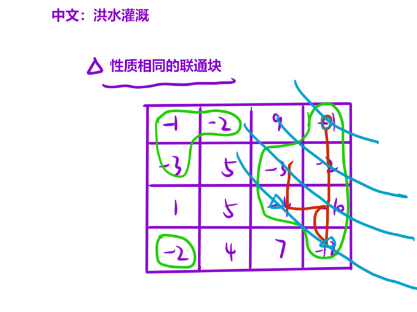
使用BFS算法大前提：只能解决边权为1

1.1.图像渲染

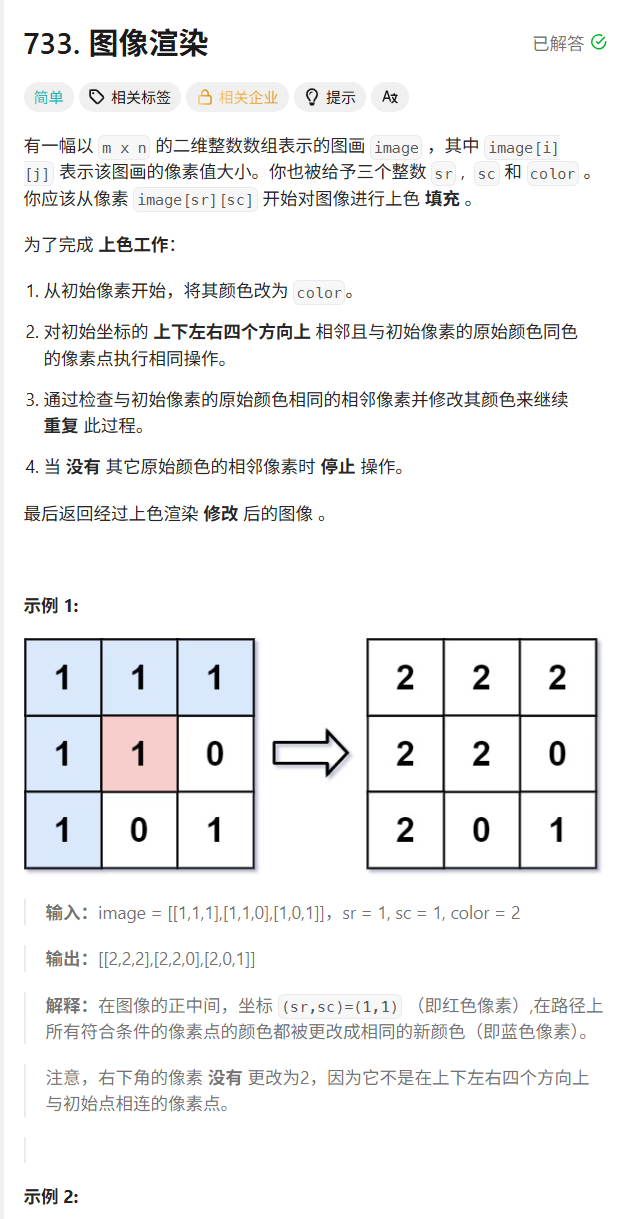
解题思路：

利用洪水灌溉的思想，借助队列,一层一层的向四周进行灌溉

代码实现：

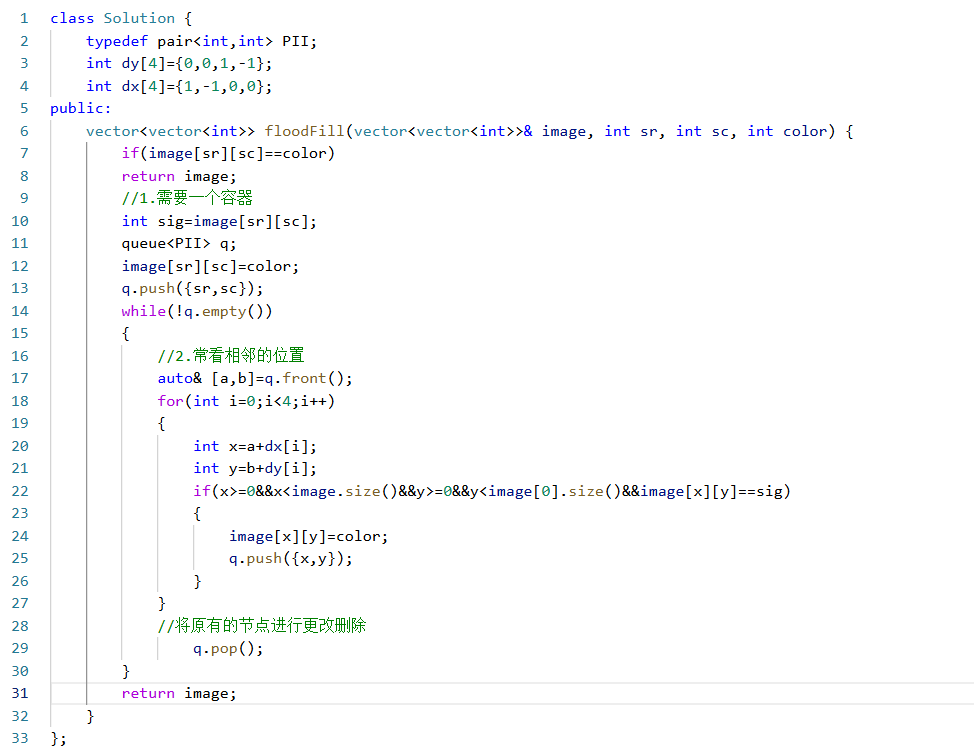
注意点：

在对队列之前，你就要将入队列的元素进行更改，防止重复入队列，导致死循环

1.2.岛屿数量

解题思路：

问我们岛屿的数量，其实就是问我们图中有有多少个聚集的“1”，所以我们其实就可以将整个数组进行遍历一遍，遍历一遍的话我们会遇见第二个问题就是如何避免重复记录，

所以

此时我们就要定义一个标记数组，将已经记录过的位置进行标记，

而然，

标记的方法就是使用bfs进行灌溉，将整个岛屿进行覆盖

代码实现：

细节处理：

使用memset进行对标记数组的初始化

1.3.岛屿的最大面积

解题思路：

上道题求解的是岛屿的数量，这道题求解的是岛屿的最大面积，其实我们在遇见一个新的岛屿的时候，记录岛屿的面积，在最后在对岛屿进行更新即可，其他逻辑上都是一样的

代码实现：

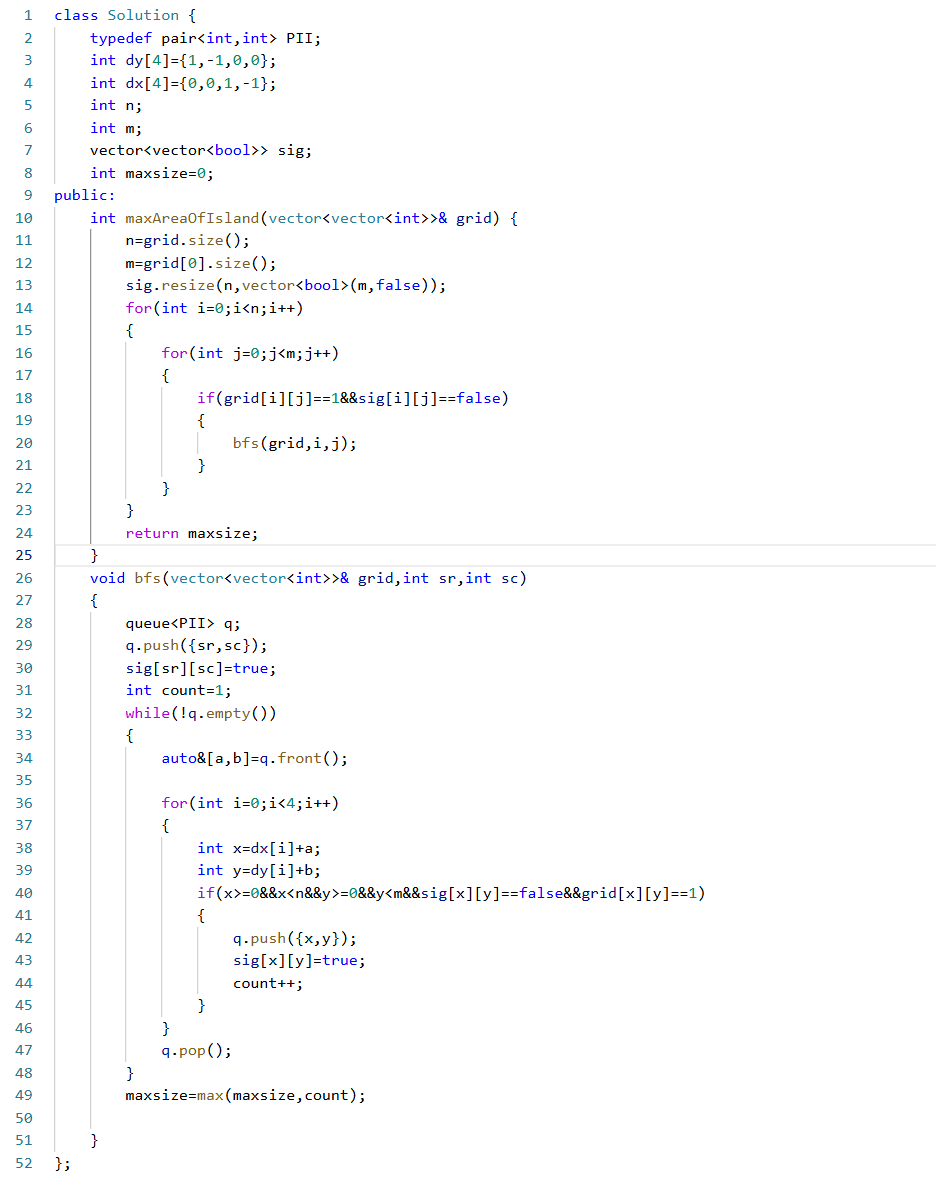
细节处理：

与上道题相同

1.4.被围绕的的区域

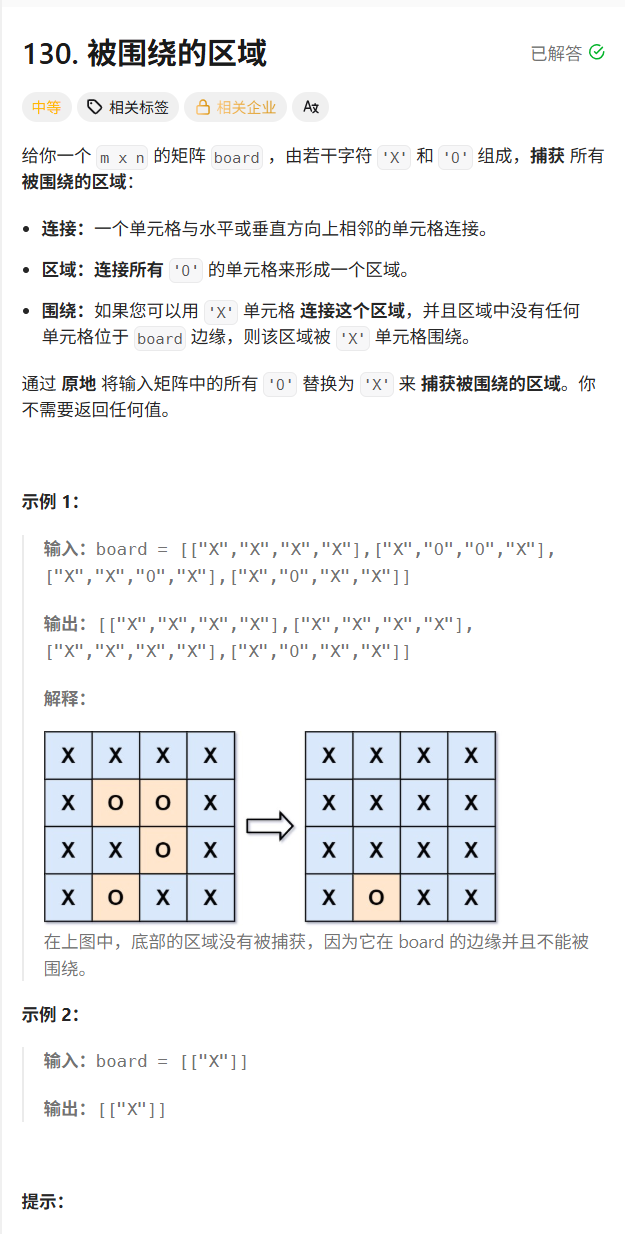
解题思路：

要将包围的岛屿进行同化处理，但是岛屿处于边界的时候是不可以进行更改的，

按照之前的思路我们直接对整个地图进行遍历一遍，

此时就会遇见一个问题就是使用bfs算法的时候是边入队列，边进行更改，

但是此时我并不知道这个岛屿集合中是否包含边界岛屿，所以发现包含边界岛屿又进行改回是以将很麻烦的时候，所以直接进行遍历是不行的。

正难则反，我们要改变的是包围岛屿，不改变边界岛屿，

所以此时我们就可以对边界岛屿使用bfs算法，

对这些边界岛屿集合进行标记，然后再将剩余的岛屿全都进行淹没，

在将标记岛屿进行改回，此时就是我们最终的结果

代码实现：

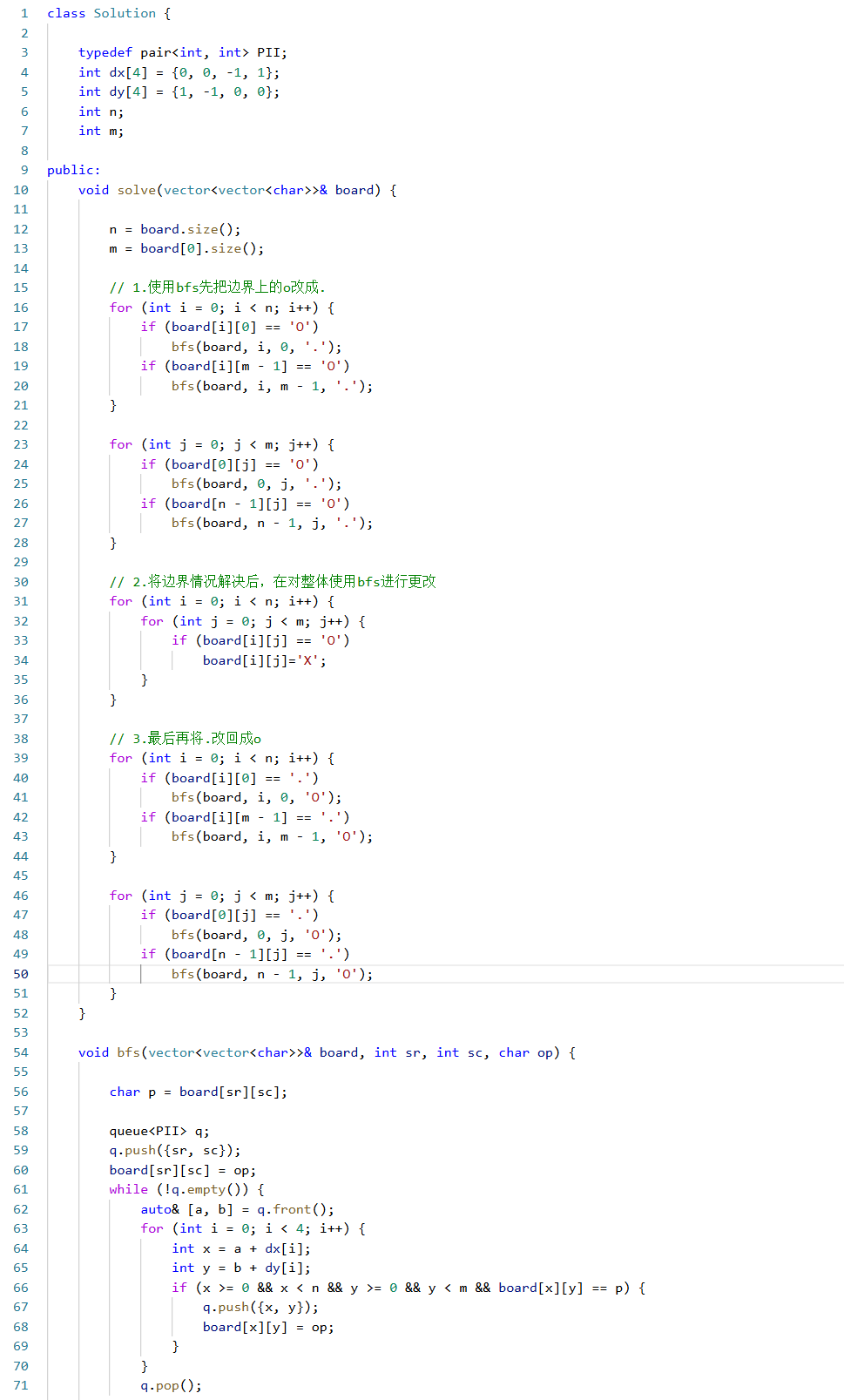
细节处理：

如何遍历矩形的边界？

2.BFS解决单源最短路径问题

2.1.迷宫中离入口最近的出口

解题思路：

这道题的思路其实利用bfs一层一层的遍历和队列的特性先进先出，一层一层存储，

所以我们可以从给定的初始位置进行bfs，将一层中所有的元素都入队列，

并记录这一层的个数，一次性将一整层的元素给出队列，

并且每次出完一层的元素后步数进行step++

每次出元素的时候就判断这个元素是边界位置（起点除外），如果是直接返回step即可

当队列为空的时候还是没有找到出口，返回-1（没有出口）

代码实现：

细节处理：

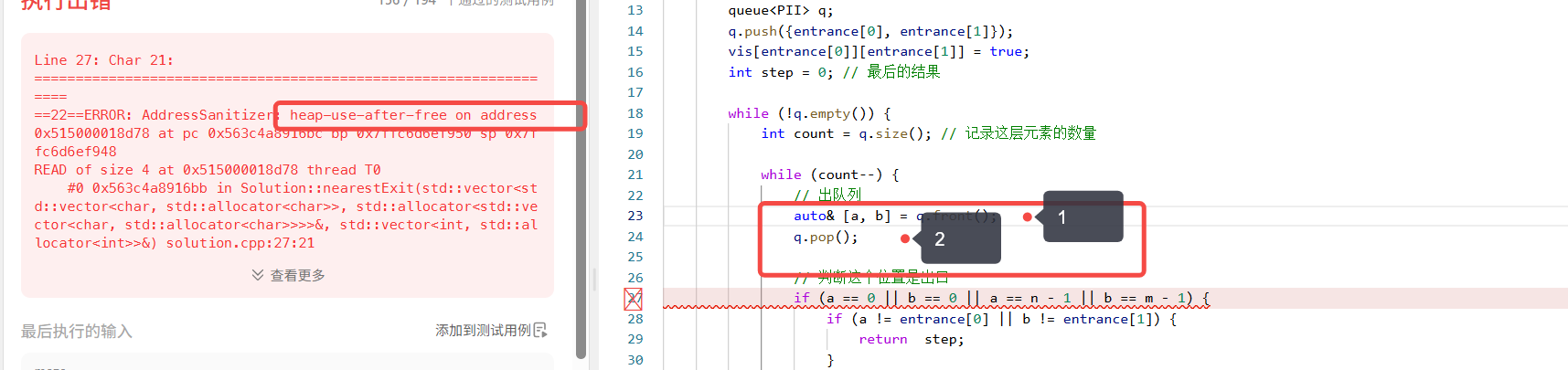
1.在用auto接受队列首元素地址的时候，不可以用引用，因为后面就是pop出队列所以，出队列以后再次进行访问的话，就会出现非法访问的警告

2.2.最小基因变化

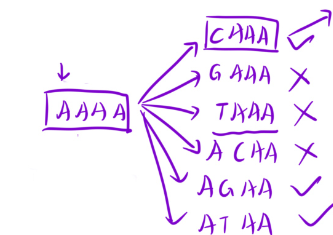
解题思路：

其实这道题可以转化成边权路径为1 问题 -》》bfs

给定一个初始的值，对初始值的8给位置进行四种变化，其实就是向四周找路

位置

代码实现：

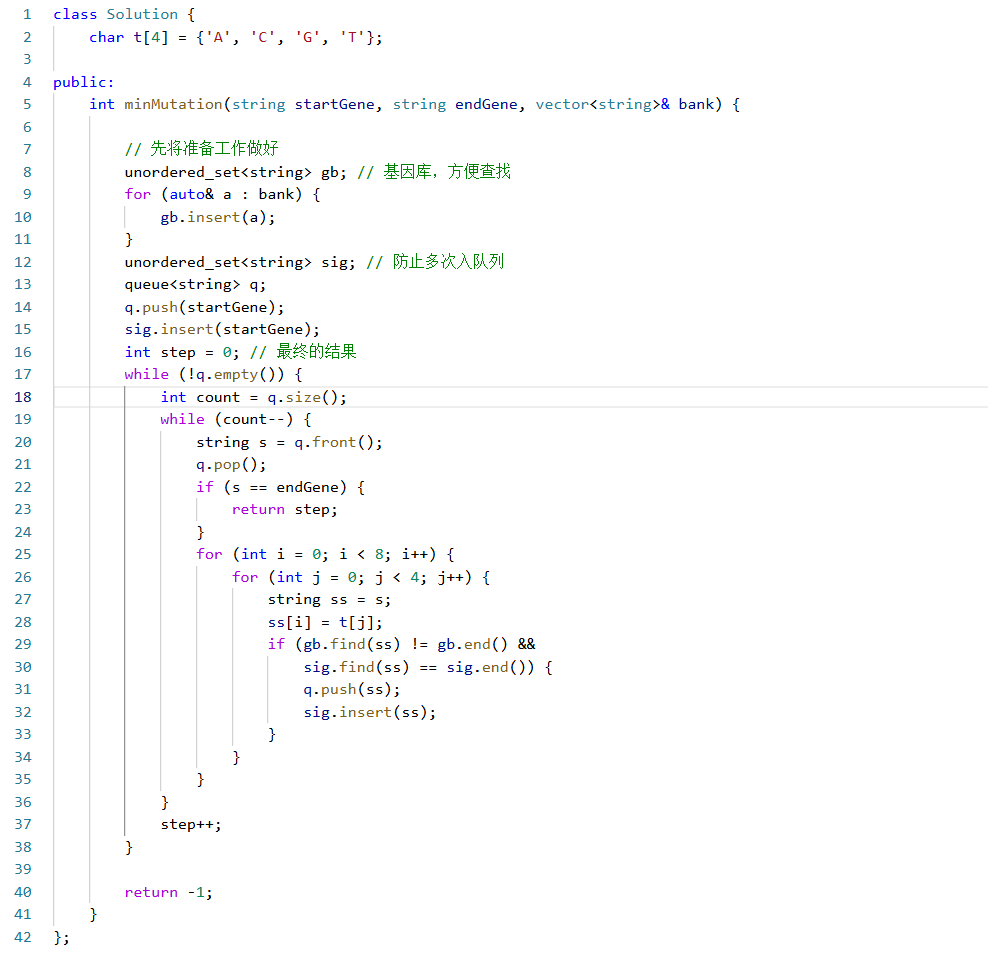
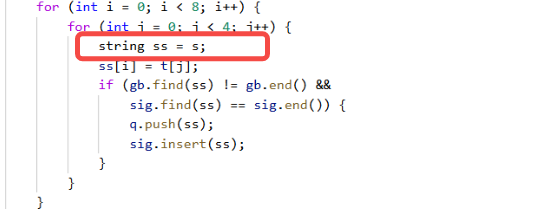
细节处理：

变化基因的时候只能变化一个位置，防止多次变化。

2.3.单词接龙

解题思路：

这道题和上道题一模一样，不做解释

代码示例：

细节处理：

2.4.为高尔夫比赛砍树

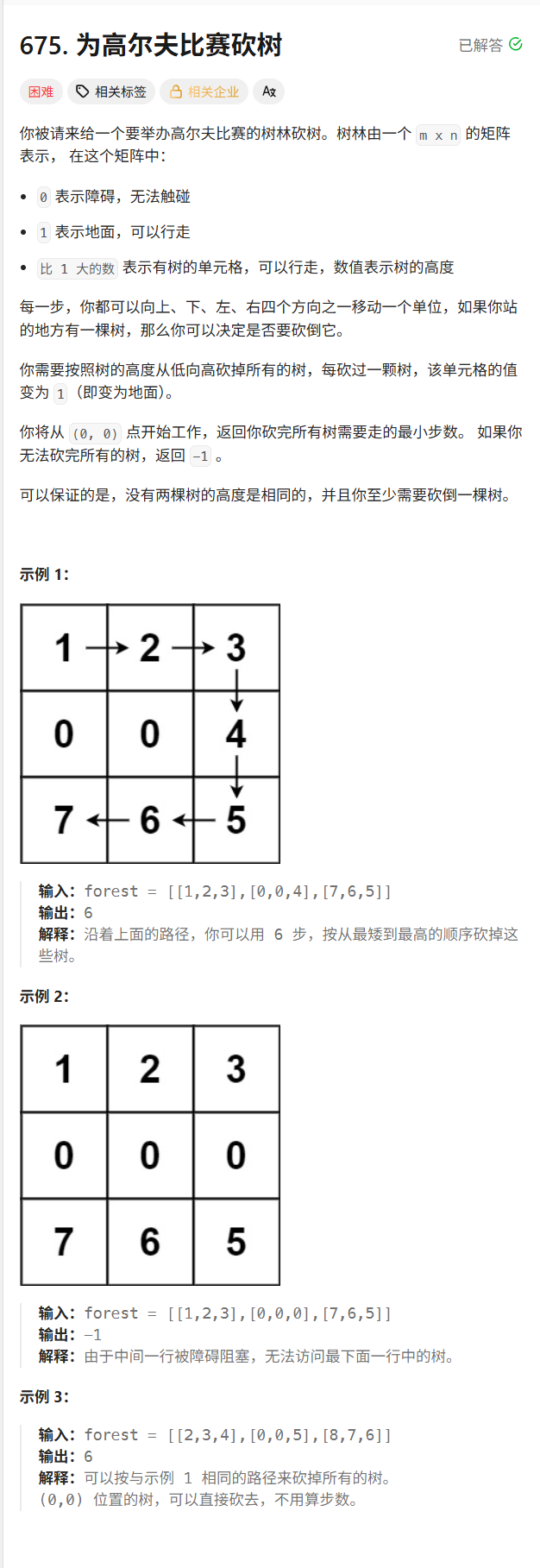
解题思路：

根据题意，要我们按照树的大小根据一定的顺序进行砍树，就是从一个起始点到另一个位置的过程，

注意：让我们求从一个起始位置到另一个位置的最短路径==>>迷宫最小路径问题

ok，有了这个思想，最终我们只需关注两点：

1.（一开始的位置是 0，0）当我找到目标位置的时候，我只需更新现在的位置为起始位置，然后在去找下一个目标位置，循环重复不断地更新起始位置

2.每一次循环都要记录此次地最短路径，然后进行累加

代码实现：

细节处理：

1.每次使用标记数组之前，一定要将之前的数据全都清空（只用resize（）一个进行设置的话是不行的）

3.BFS解决多源最短路径路径问题

解决多源方法：

考虑两种解决方法：

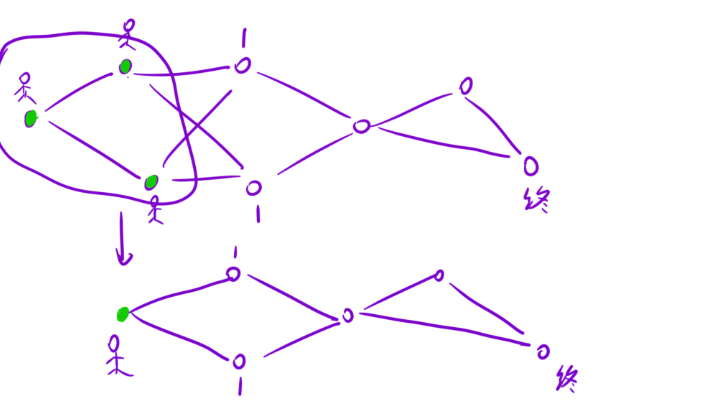
解法一:暴力，把多源最短路问题转化成若干个单源最短路问题，大概率是会超时的

解法二:把所有的源点当成一个"超级源点”、

解法二的代码实现：

3.1.矩阵

解题思路：

解法一:一个位置一个位置求（多个单源的bfs），超时

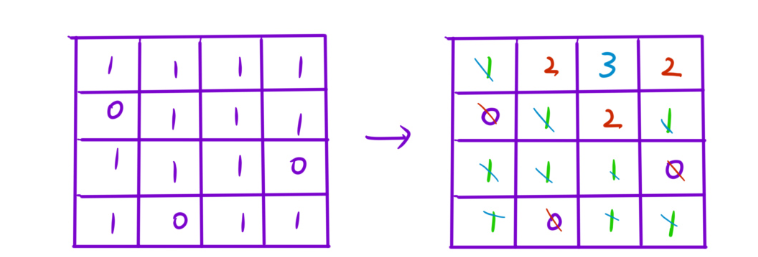
解法二:多源 BFS + 正难则反

正难则反：把所有的 0 当成起点，1当成终点，（如果把1当作起点的话，我求出最短路径后，并不知道是哪个”超级源点的的最短路径“）

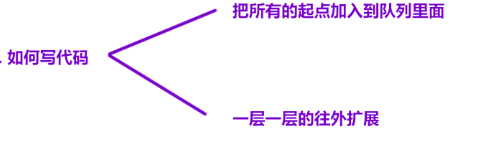
1.把所有的 0 位置加入到队列中
2.一层一层的向外扩展即可

代码实现：

细节处理：

1.reusul数组的两种用法

   1.一开始都初始化为-1，可以标记是否入过队列

    2.result记录的是step，所以我们无需记录步数（一层的个数）

2.此时因为0是起点，所以我遇见1的时候就直接将我上一层的最短路+1就是这个节点的结果

3.2.飞地的数量

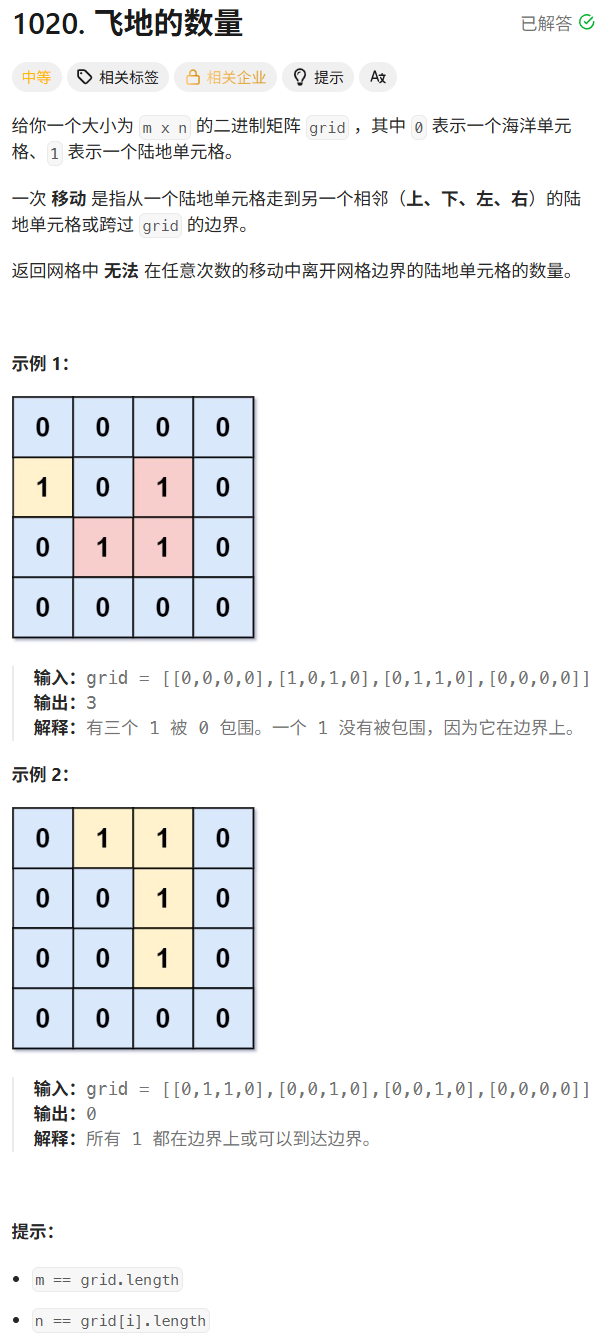
解题思路：

当我看到这道题的时候，一联想起来的就是”被围绕的区域“这道题，

这道题其实可以使用相同的思想正难则反

我不对无法出去的飞地进行统计，而是对可以出去的飞地进行统计（矩形的边界）

所以此时我们可以有两种做法：

1.单源的bfs：遇见一个陆地就进行bfs

2.多源的bfs：先将所有的边界飞地入队列形成“超级源点”（我们采用的是多源）

  

   A .先将所有的边界陆地加入到队列当中，形成超级源点

  B.超级源点进行bfs遍历

  C.统计还没有被遍历到的陆地

代码实现：

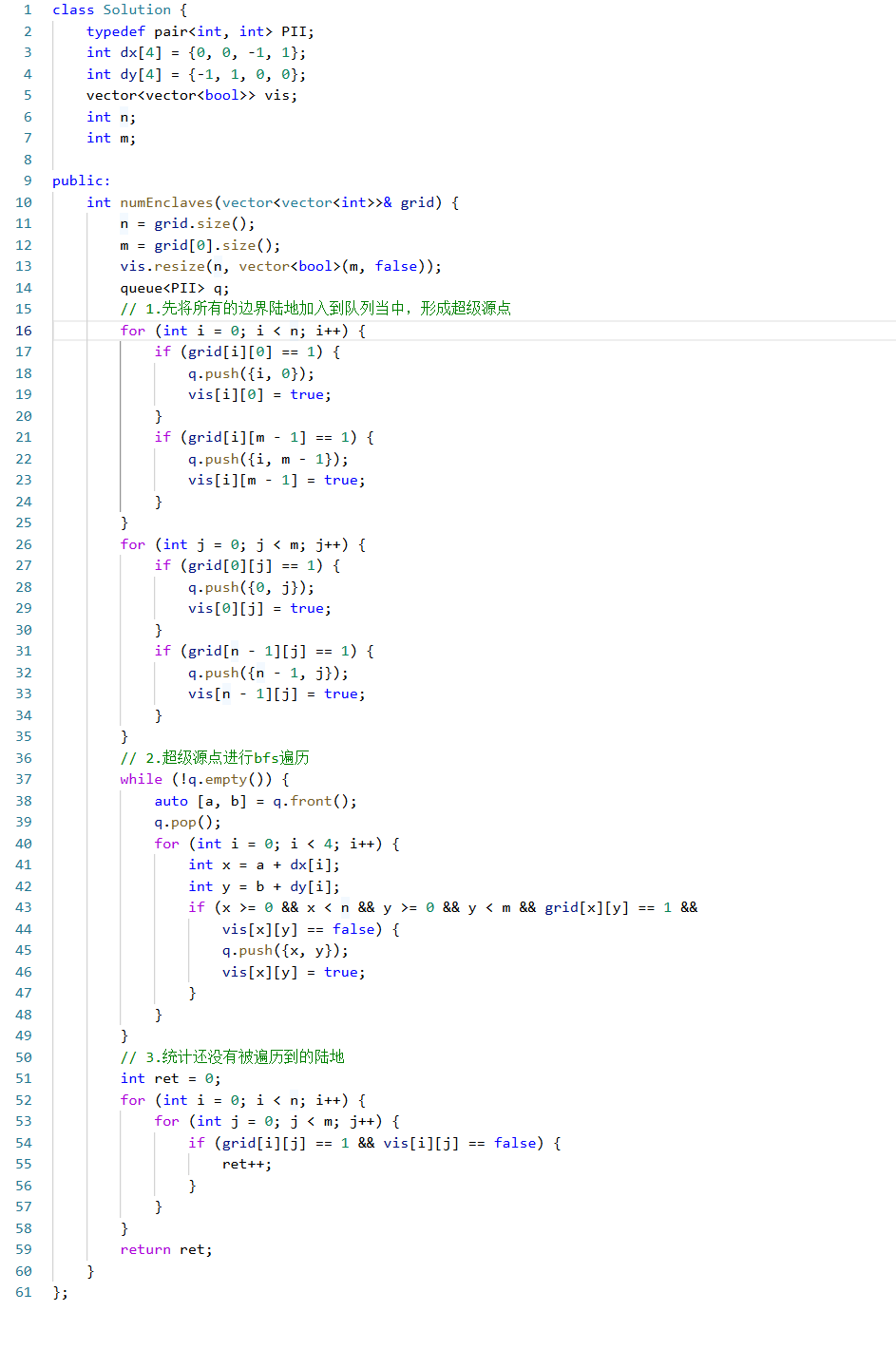
细节处理：

3.3.地图中的最高点

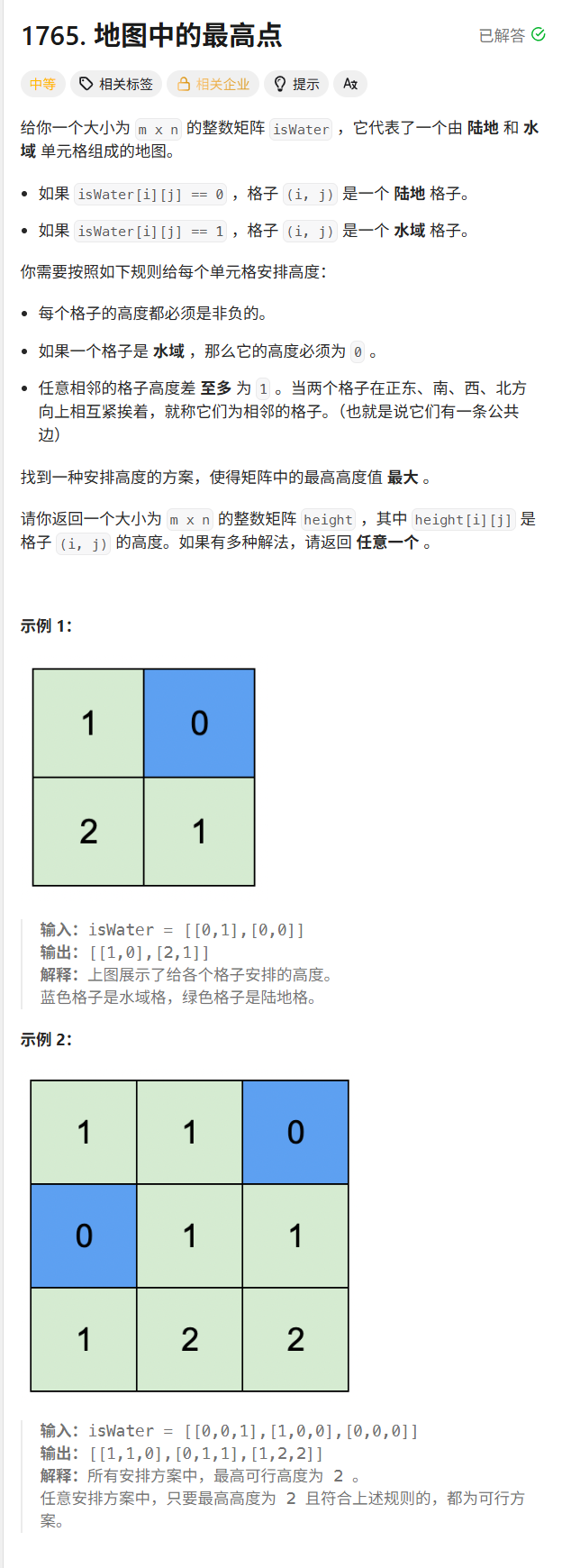
解题思路：

这题和矩阵这题一模一样，只是换了一种说法，不做解析

代码实现：

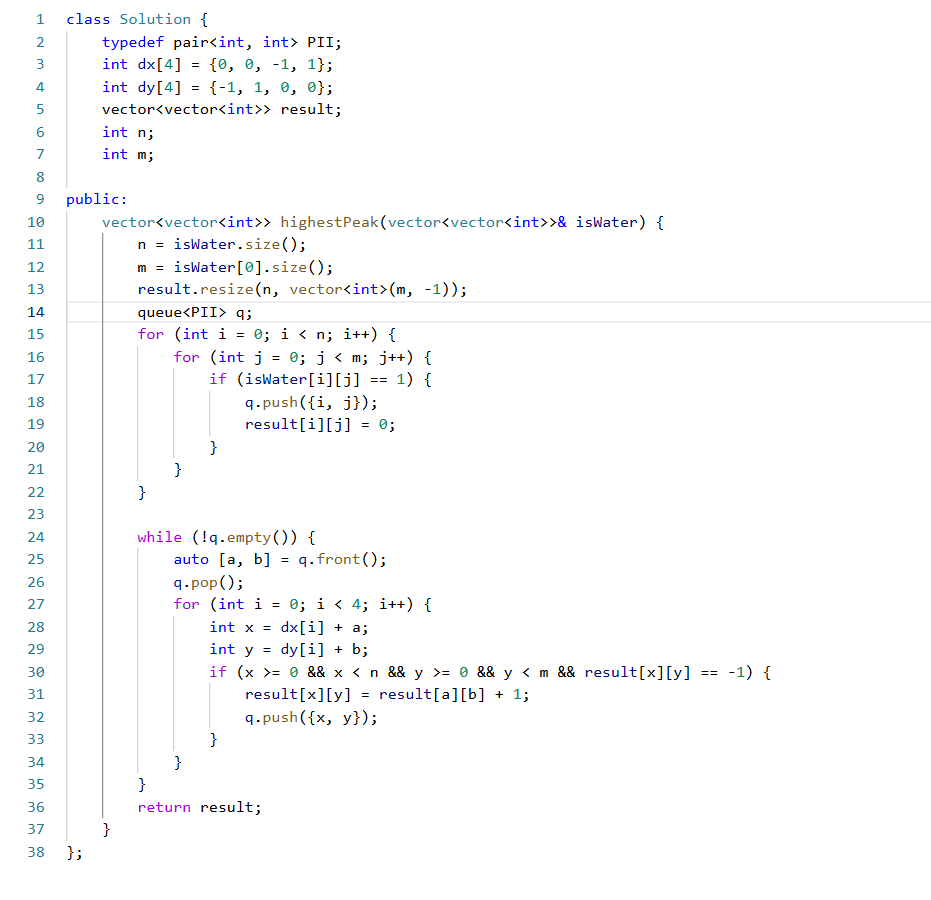
细节处理：

3.4.地图分析

解题思路：

依旧是和第一题一样，也是换种说法，不做解释

代码实现：

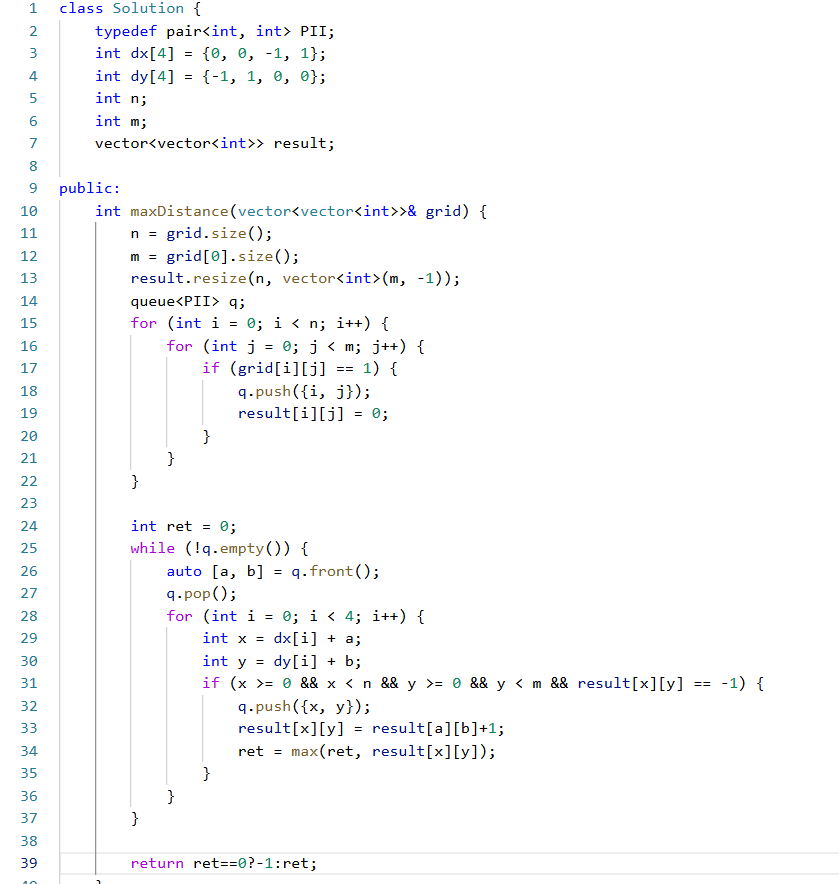
细节处理：

4.解决拓扑排序

拓扑排序的简介：

1.有向无环图（DAG图）

边是有方向的，但是不可能构成一个回路，就是一个DAG图

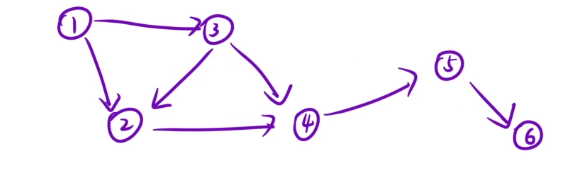
反例：4 ，5 ，6，这几个节点就构成了一个回路，所以他就不是一个DAG图

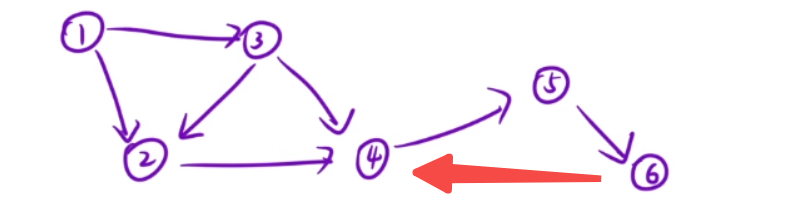
入度和出度的概念：

入度：有多少个边指向这个节点   一号：0

出度：有多少的个边从这个节点出去  一号：2

2.AOV图：顶点活动图

在有向无换图中，用顶点来表示一个活动，用边来表示活动的先后顺序的图结构

AOV 图是 DAG 的一种具体应用，专注于表达活动之间的先后约束关系。

比如这样的一种流程图就是一个AOV图

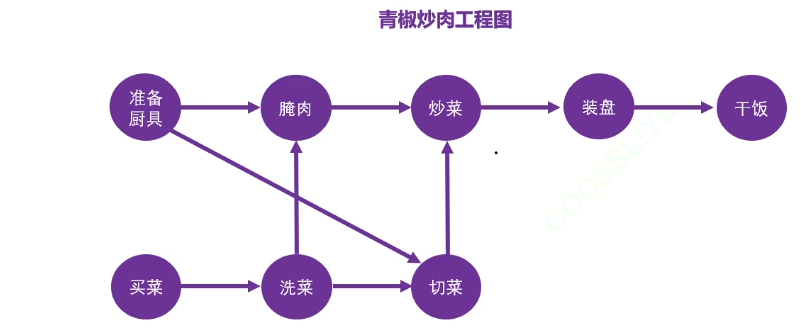
3.拓扑排序

拓扑排序的一个重要应用就是判断 一个有向无环图中是否有环

4.实现拓扑排序

4.1.课程表

解题思路：

题意：

假设题目给定的数据是这样的：

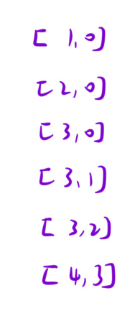
那么下面就是我们要建图的效果：

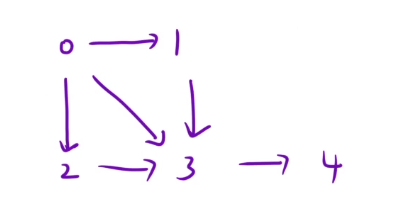
所以此时我们就会遇到一个问题如果进行建图？

建图的方法有三种：

下面主要讲解的是使用邻接表的方式：

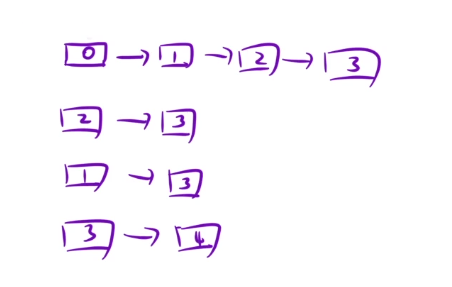
这种方式又可以借助两种不同的STL容器：

1.vector<vector<int>> ;

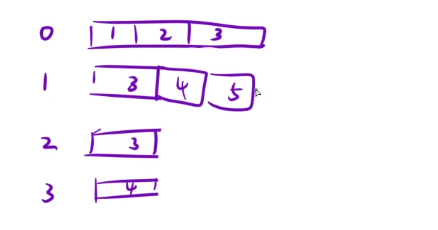
0号下标就表示数字0指向的节点。

1号下标就表示数字1指向的节点。

2号下标就表示数字2指向的节点。

3号下标就表示数字3指向的节点。

.

.

.

但是这个有个缺陷就是如果对于是string类型的节点，还要做一组string 和 int 类型的映射

2.unordered_map<<int,vector<int>>;

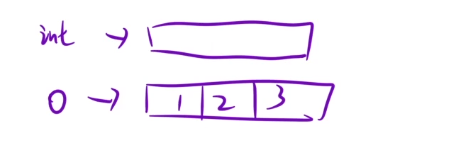
哈希表的话就比较万能，就没有之前的那种顾虑，直接是一个key -value的模型

回归主题，这里询问的是是否能完成所有的课程，起始就是在询问这个DAG图中是否有环

代码实现：

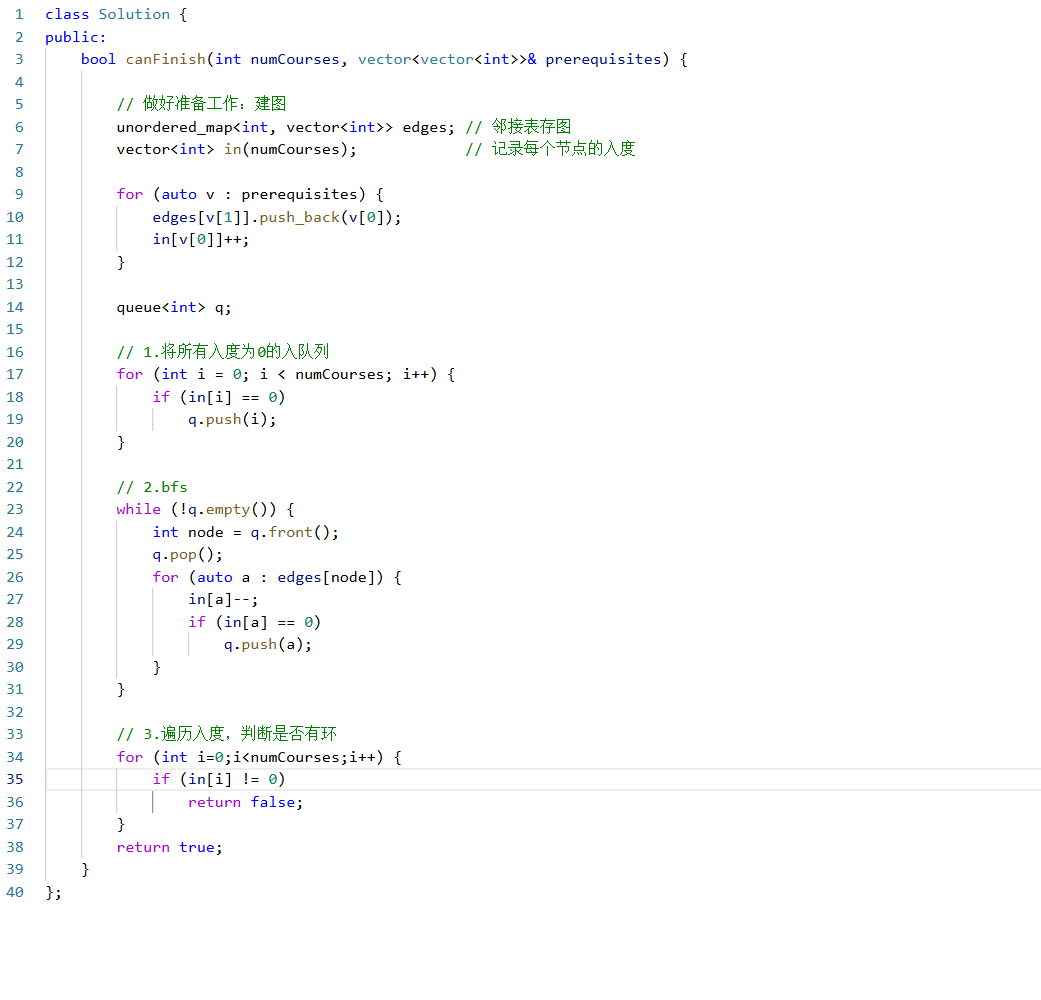
细节处理：

4.2.课程表||

解题思路：

和上道题没区别不做解释

代码实现：

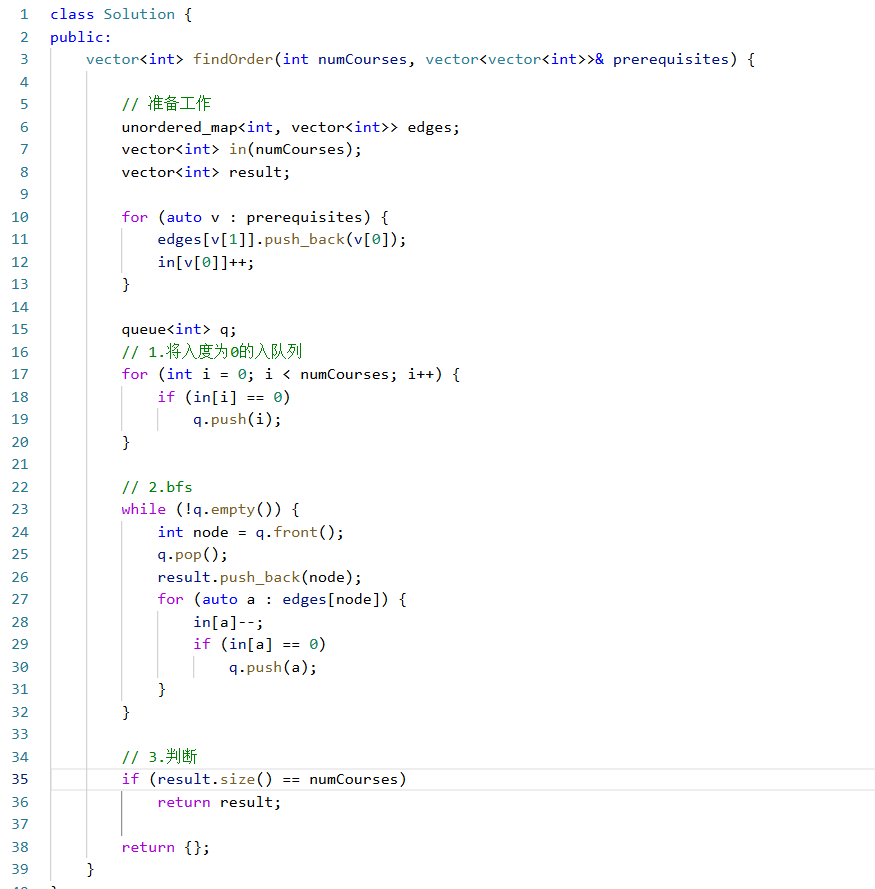
细节处理：

最后判断的时候可以直接比较结果和总课程的大小，无需进行遍历数组，

空数组的话，返回一个{}，它会自动进行转化

4.3.火星单词

解题思路：

题目意思：就是让我们根据它们排好序的单词表来推断出这个火星真正的字母排序大小

所以我们可以根据已有的单词表使用两层for，利用它们给定的规则，进行构图，

最后，再次使用拓扑排序

代码实现：

细节处理：

1.记录数据阶段：

A.如何已经对两个不同的字母进行排序后，这两个单词后面的字母不需要看了，直接break

B.两个字母的关系已经存贮在hash表中的时候，也是直接break

C.非法情况：[”abc“，”ab“]:直接返回空

2.如果有环的话也是直接返回空