π是不是真的包含了我们每个人的银行卡密码？

细思极恐

既然圆周率是无限不循环小数，那么其中是否可能包括这个世界上可用数字描述的任何信息，也就是包含了这个世界？

电话号， 生日， QQ号可能运算量比较大，但是6位的银行卡密码还是没问题的。题目本身和Pi是不是正规数没关系，但假如承认 Pi 是个正规数会有帮助

这相当于问一个产生六位随机数的发生器多久能生成所有六位数？

这是赠券收集问题 ，那么期望就是  ，H 是调和级数

所以我算这么多大概就能搜索到所有的可能

嗯，真的把十万个个全部搜出来了

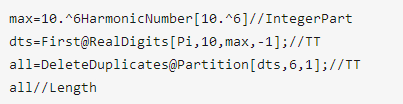
加起来也就一分钟就不另外放下载了，自己跑一遍就行

---

当然你说要是没搜到怎么办？

这倒是有可能的，但是还是根据赠券收集原理

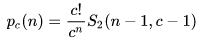
搞定的概率只有：57%

我在想这个数好眼熟....

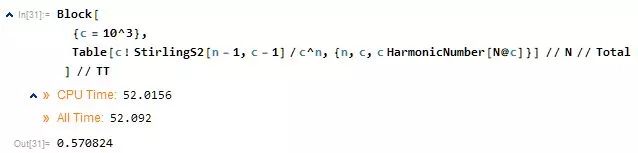
这个数是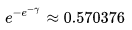 

如果要以一半概率找到生日的话需要计算3.51亿位，如果要找手机号要计算4606亿位

查了下现在的记录是22,459,157,718,361（224591亿位）， 那么找到手机号的几率>99.9%

http://www.numberworld.org/digits/Pi/#Download

另外很多网站都提供这个服务

---

当然一个非超越无理数以概率1是个正规数，那么同样适用这样的推理

我的生日是你的生日开平方后351084058位开始8个数字
我的手机是你的手机号开立方后460653489114位开始11个数字

---

57% 怎么推导出来呢?

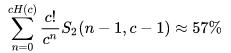
但是有个问题，斯特林数有精细结构没法给出渐进表达式

那么考虑非均匀赠券收集问题

记事件 An,i 为第$n$次选取后第$i$个样本未被选中的情形,于是概率即为相应情形之并

然后依容斥原理展开：

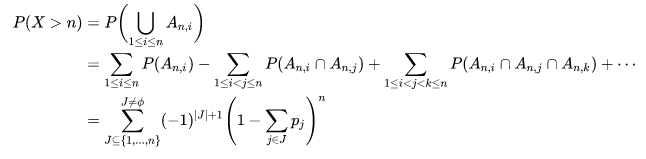
其中，$J$代表一种选法集合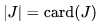， ，即集合$J$中元素的数量。

其概率生成函数为：

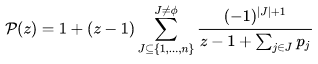
接下来对于期望而言：

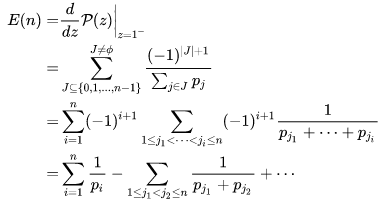
注意到  

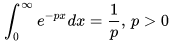
所以上式可以进一步可以写成：

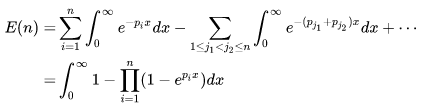
另一方面从累积分布而言：

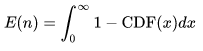
于是令 

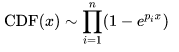
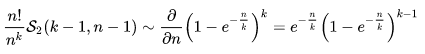
我们成功把问题转化为连续情形：

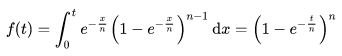
其中 n 为规模，t为计算的位数

其一阶近似就是 n H(n)

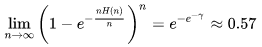
这也是临界情况，加一个微扰全部找到的概率就是1，减一个微扰概率就是0。

算10亿位还找不全的概率几乎为0

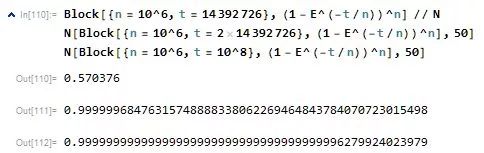
本文由超级数学建模编辑整理

资料来源于酱紫君（知乎）

https://www.zhihu.com/question/23419402/answer/329851843

转载请在公众号中，回复“转载”

1.在美国的电子工程师眼中的中国电子行业！

2.Python难懂？买一次西瓜就懂了！

3.电路板设计为什么要设置这些测试点？

4.掌握这些，就能成为嵌入式开发多面手！

5.从Intel和ARM争霸战, 看看做芯片到底有多难

6.重拾uC/OS-II之任务机制理解

免责声明：本文系网络转载，版权归原作者所有。如涉及作品版权问题，请与我们联系，我们将根据您提供的版权证明材料确认版权并支付稿酬或者删除内容。