Python--Poisson学习笔记

Poisson distributed data

import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import multivariate_normal, poisson
from argparse import Namespace
from iminuit import Minuit
from functools import lru_cache
import joblib

def run(k):
    m = Minuit(lambda lambd: -poisson.logpmf(k, lambd), lambd=k + 1)
    m.limits["lambd"] = (0, None)
    m.errordef = Minuit.LIKELIHOOD
    m.migrad()
    m.hesse()
    m.minos()
    assert m.valid
    p = m.values["lambd"]
    dp = m.errors["lambd"]
    pm = max(p + m.merrors["lambd"].lower, 0.0), p + m.merrors["lambd"].upper
    r = p, dp, *pm
    return r

rng = np.random.default_rng(seed=1)
nmc = 5000
mu = 10 ** np.linspace(-1, 2, 100)
pcov = {"HESSE": np.empty_like(mu),"MINOS": np.empty_like(mu),}

for i, mui in enumerate(mu):
    nh = 0
    nm = 0
    for imc in range(nmc):
        k = rng.poisson(mui)
        p, dp, pd, pu = run(k)
        if p - dp < mui < p + dp:
            nh += 1
        if pd < mui < pu:
            nm += 1
    pcov["HESSE"][i] = nh / nmc
    pcov["MINOS"][i] = nm / nmc
fig, ax = plt.subplots(1, 2, figsize=(9, 4))
plt.sca(ax[0])
n = np.arange(101)
interval = {"HESSE": np.empty((len(n), 2)),"MINOS": np.empty((len(n), 2)),}
for i, k in enumerate(n):
    p, dp, pd, pu = run(k)
    interval["HESSE"][i] = (p - dp, p + dp)
    interval["MINOS"][i] = (pd, pu)
for algo, vals in interval.items():
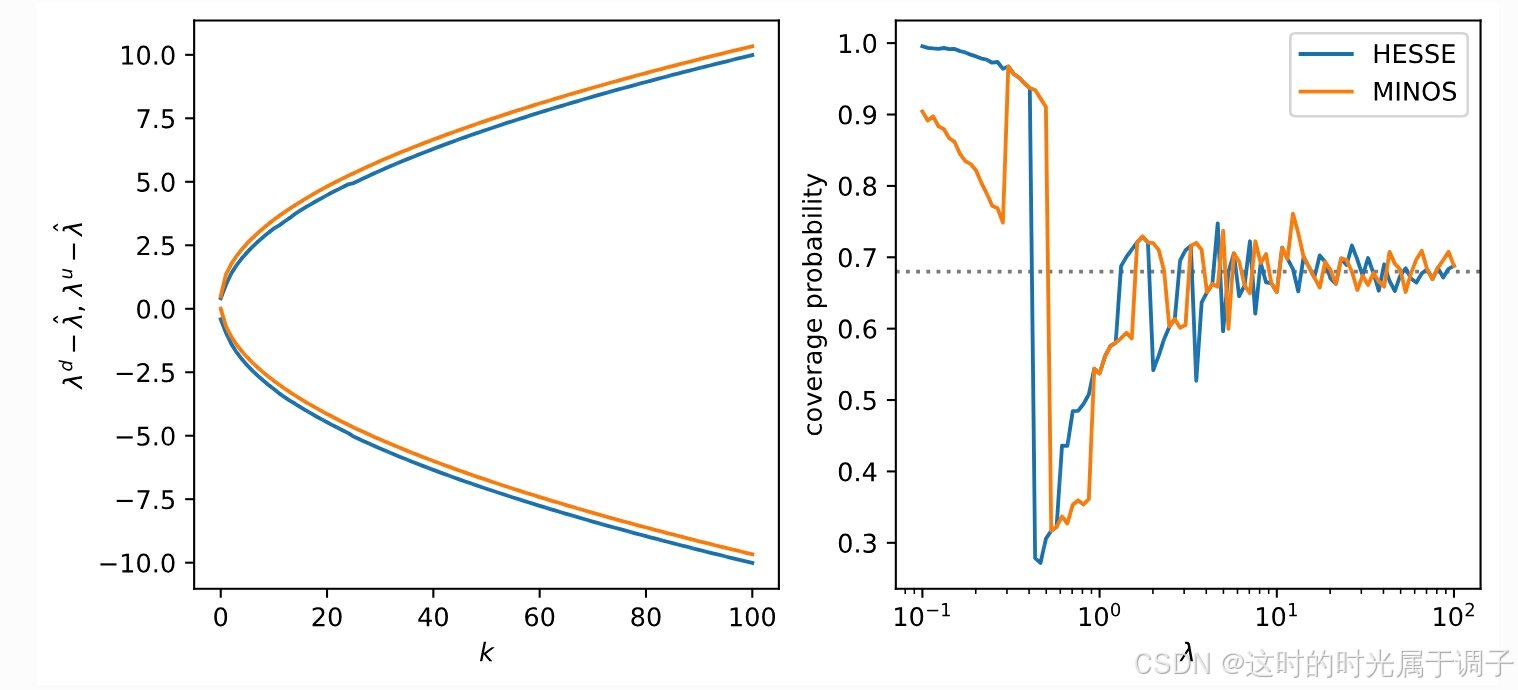
    plt.plot(n, vals[:, 0] - n, color="C0" if algo == "HESSE" else "C1", label=algo)
    plt.plot(n, vals[:, 1] - n, color="C0" if algo == "HESSE" else "C1", label=algo)
plt.xlabel("$k$")
plt.ylabel(r"$\lambda^d - \hat\lambda$, $\lambda^u - \hat\lambda$")
plt.sca(ax[1])
for algo, vals in pcov.items():
    plt.plot(mu, vals, label=algo)
plt.axhline(0.68, ls=":", color="0.5", zorder=0)
plt.xlabel(r"$\lambda$")
plt.ylabel("coverage probability")
plt.legend()
plt.semilogx()