BP神经网络算法的数学推导和Matlab实现

首先声明，这篇文章不是神经网络的扫盲文，如果只想知道神经网络的概念那笔者还是推荐找一些深入浅出的文章来看。但是如果需要自己实际搭建和使用一个神经网络，同时具备一定的数学功底的话，那这篇文章就是为了深入的剖析神经网络算法的工作过程和模型而写的。这里笔者把整个神经网络的工作过程由特殊情况推广到一般情况，让读者了解整个神经网络的工作过程，并且给出实际搭建一个神经网络的方法。希望有意愿了解的读者能够拿起笔跟着文章一起把公式写一遍。作者也是边推导公式边整理思路，最后从只有概念性的认识到能够自己搭建一个Matlab的神经网络架构。

神经网络必备的基础的数学知识：

梯度：
相较于单变量的函数，梯度和导数的含义是一样的，但是对于一个多变量的向量来说，其梯度的含义就是在某点处变化最快的向量场，例如对于一个三元函数t=f(x,y,z)来说，其在空间某点的梯度就是：

链式法则：
链式法则常用于复合函数求导问题

神经网络算法：

神经网路算法灵感来源于生物细胞中的神经元结构，神经元具有树状突触用来和其他神经元进行交流，在数学上突触就可以视为信号的来源和对象。不同神经元之间的树状突触大小可能不同，不同大小的突触对于信号的响应程度也不同，在数学上对于信号的响应程度就可以用权值来表示。对于相互交流频繁的神经元其之间的突触连接更加紧密，对应的也就是其信号的权值较高。神经元对得到的信号进行总结，在数学上就是对所有输入信号乘以各自的权值后求和。神经元在对总结好信号进行处理，判断是否需要输出生物电信号，在数学上就是将求和的信号作为代入到某个函数中，得到函数结果，根据结果决定输出值。一个神经元可以有多个输出对象，但是只有一个输出结果，也就是相同的输出结果可以输出给多个输出对象。

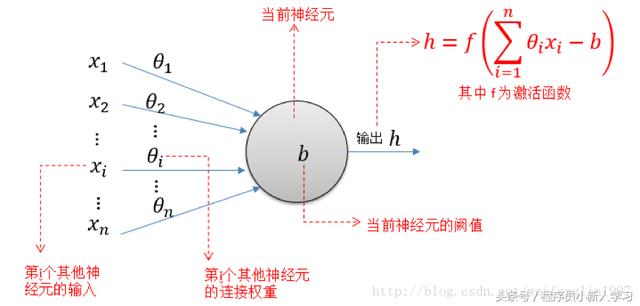
如图所示归纳出一个神经元的数学模型，一个神经元有多个输入x1、x2…xn，每个输入对应了各自的权值k1、k2…kn，则其输入的加权和为

$$s_i=x_1\ast k_1+x_2\ast k_2+......x_n\ast k_n$$

假设其输入的偏置为b，则实际的加权和为

$$s_i=x_1\ast k_1+x_2\ast k_2+......x_n\ast k_n+b$$

现在，输入变量的表达式得到了，那输入和输出的关系，即函数f()怎么得到呢？一般来说，考虑到输出的结果在0到1的范围内，而输入的结果的取值范围则为实数域，因此需要一个函数其定义域为实数域，值域为0到1，常见的函数有阶跃函数、sigmoid函数等，将$s_i$带入函数中，得到的结果就是神经元的输出h。这里输出的值只有一个，但是输出的对象可以有多个。

在了解单个神经元的数学模型后，将多个神经元组合起来形成网络，就是神经网络。神经网络的组成主要有三部分。对于没有其他神经元的输入，只有输出的神经元，往往在第一层作为感受器而存在，这一层叫做输入层。对于没有其他神经元的输出，只有别的神经元对其输入的神经元往往在最后一层作为执行器而存在，这一层叫做输出层。而中间既有神经元的输入又有神经元的输出的均为隐层。一般来说输入层和输出层只有一个，但是隐层可以有多个。

为了方便数学模型的表示，我们对于各层之间的变量进行一个命名。对于某一层的某一个神经元，与之相关的参数有：来自上一层的输入和权值和对下一层的输出和权值，以及其输入的加权和，还有该神经元的处理函数。

如图所示，对于第M层的第j个神经元，其输入的加权和为$s_j^M$，表示第M层的第j个神经元的加权和s；其输出为$x_j^M$，表示第M层的第j个神经元的输出x；而第L层的第i个神经元和第M层的第j个神经元之间的权值为$k_{i-j}^M$；而第M层的处理函数可以写为$f_M()$。由此一个神经元有关的变量就全部都能表示了。

根据上面所讲述的神经元的知识，可以得到，对于第M层的第j个神经元，有以下关系方程

1.来自上一层的输入乘以对应的权值得到该神经元的加权和
$$s_j^M=x_1^L\ast k_{1-j}^L+......x_i^L\ast k_{i-j}^L+......x_l^L\ast k_{l-j}^L$$
用累加来表示，可以写成
$$s_j^M=\sum _{i=1}^l(x_i^L\ast k_{i-j}^L)$$

2.对加权和进行函数处理得到该神经元的输出
$$x_j^M=f_M(s_j^M)$$

由此可以类推出任意层的任意一个神经元的关系方程。

在信号的正向传递中，所有的信号经过一个个的神经元，在上述关系方程的计算下层层累积最终对输出造成影响。

这里，对于神经网络来说，在一次神经网络计算过程中，其各个神经元之间的权值的变化将会导致输出的变化，为了得到一个较为理想的输出，就要改变其各个神经元之间的权值，从而最终得到一个合适的输出，使得该输出和理想输出的差值最小。这就变成了一个数学上求最值的问题，最值的对象是偏差值，也就是求偏差值最小值。其自变量就是神经网络中的各个神经元之间的权值。对于这种多变量的函数，求最值的问题就关系到了文章开头所说的梯度。也就是求出在当前权值组合下偏差对于各权值的梯度，然后按照与梯度相反的方向，稍微修改权值，；然后再计算该权值下的梯度，然后按照与梯度相反的方向修改权值，重复上述步骤一直到输出偏差到达最小值。这就是为什么神经网络算法又是一种学习算法的原因，因为它会自己不断的趋向最优的结果。

但是这里存在一个问题，就是有可能最终得到的结果只是一个局部最优解，而不是全局最优解。对于这种情况可以通过设定初始权值，惯性等来避免，这里先不进行阐述。

现在对上述求梯度这一过程给出数学上的表达。这里也是神经网络算法反向传递的精髓所在。

首先以一个3-4-2的神经网络为例，然后类比成a-b-c的神经网络，然后再类比成更多层的神经网络。

首先输入通过正向传递到达输出，这里我们先一第二层的第一个和第三层的第一个为例：

第2层第1个神经元：

$$s_1^2=x_1^1\ast k_{1-1}^1+x_2^1\ast k_{2-1}^1+x_3^1\ast k_{3-1}^1$$

$$x_1^2=f(s_1^2)$$

类比出第2层第j个神经元：

$$s_j^2=x_1^1\ast k_{1-j}^1+......x_i^1\ast k_{i-j}^1+......x_a^1\ast k_{a-j}^1=\sum _{i=1}^a{x}_i^1\ast k_{i-j}^1$$

$$x_j^2=f(s_j^2)$$

第3层第1个神经元：

$$s_1^3=x_1^2\ast k_{1-1}^2+x_2^2\ast k_{2-1}^2+x_3^2\ast k_{3-1}^2+x_4^2\ast k_{4-1}^2$$

$$x_1^3=f(s_1^3)$$

类比出第3层第k个神经元：

$$s_k^3=\sum _{j=1}^b{x}_j^2\ast k_{j-k}^2$$

$$x_k^3=f(s_k^3)$$

对于输出，这里的神经网络计算得到的输出是$x_1^3$和$x_2^3$，当理想的输出已知，且为y1和y2时，我们能计算得到输出的偏差（这里的系数1/2是为了后续求导的时候抵消因求平方的导数带来的系数2）

$$E=\frac{1}{2}(x_1^3-y_1{)}^2+\frac{1}{2}(x_2^3-y_2{)}^2$$

对于a-b-c的神经网络，类比上式可以得到：

$$E=\frac{1}{2}\sum _{i=1}^c(x_k^3-y_k{)}^2$$

到此，一个神经网络的正向传递已经结束，得到了神经网络的输出和偏差，下面就是反向调节，使得系统偏差最小。在简单的函数问题中，求一个函数最小值的方法通常是通过求导，得到函数的极值点并判断。对于多变量的函数，其最小值的方法不能简单的通过求导数得到，但是可以通过求梯度，并沿着梯度变化趋势的反方向修改当前值，然后再次计算，直到到达最小值。

求梯度通俗来说，就是对各个变量求偏导数得到的向量。对于误差E来说，其自变量是神经网络中的所有神经元之间的权值k，所以下面我们以3-4-2的神经网络中的$ k_{1-1}^1 $和$ k_{1-1}^2$ 为例，求其梯度，同时类比推导出对于一个a-b-c的神经网络，其第一层i神经元到第二层j神经元，以及第二层j神经元到第三层k神经元的权值的梯度。

首先是$ k_{1-1}^2$，对其进行偏导，可以得到$ \frac{\partial E}{\partial k_{1-1}^2}$，根据链式法则，我们先分析一下各函数的复合函数。

首先：

$$E=\frac{1}{2}(x_1^3-y_1{)}^2+\frac{1}{2}(x_2^3-y_2{)}^2=g_1(x_1^3,x_2^3)$$

可以看出$E$是关于$x_1^3$，$x_2^3$的函数，其中$x_1^3=f(s_1^3)$，$x_2^3=f(s_2^3)$，又有：

$$s_1^3=x_1^2\ast k_{1-1}^2+x_2^2\ast k_{2-1}^2+x_3^2\ast k_{3-1}^2+x_4^2\ast k_{4-1}^2=g_2(x_1^2,x_2^2,x_3^2,x_4^2,k_{1-1}^2,k_{2-1}^2,k_{3-1}^2,k_{4-1}^2)$$

$$s_2^3=x_1^2\ast k_{1-2}^2+x_2^2\ast k_{2-2}^2+x_3^2\ast k_{3-2}^2+x_4^2\ast k_{4-2}^2=g_2(x_1^2,x_2^2,x_3^2,x_4^2,k_{1-2}^2,k_{2-2}^2,k_{3-2}^2,k_{4-2}^2)$$

可以看出$s_1^3$是关于$x_1^2,x_2^2,x_3^2,x_4^2,k_{1-1}^2,k_{2-1}^2,k_{3-1}^2,k_{4-1}^2$的函数，$s_2^3$是关于$x_1^2,x_2^2,x_3^2,x_4^2,k_{1-2}^2,k_{2-2}^2,k_{3-2}^2,k_{4-2}^2$的函数。其中$x_1^2=f(s_1^2)$，$x_2^2=f(s_2^2)$，$x_3^2=f(s_3^2)$，$x_4^2=f(s_4^2)$，又有：

$$s_1^2=x_1^1\ast k_{1-1}^1+x_2^1\ast k_{2-1}^1+x_3^1\ast k_{3-1}^1=g_3(k_{1-1}^1,k_{2-1}^1,k_{3-1}^1)$$

其中$ x_1^1, x_2^1,x_31$是系统给定的输入，因此在进行偏差计算时不认为是一个变量，这里注意一下。同理可以得到$s_2^2,s_32,s_4^2$的函数关系式：

$$s_2^2=g_3(k_{1-2}^1,k_{2-2}^1,k_{3-2}^1)$$

$$s_3^2=g_3(k_{1-3}^1,k_{2-3}^1,k_{3-3}^1)$$

$$s_4^2=g_3(k_{1-4}^1,k_{2-4}^1,k_{3-4}^1)$$

又上述函数关系式可以得到各变量之间的求导关系，并利用开始提到的链式法则就能求出对任意一个变量的偏导数：

如图所示得到了一个链式法则的变量的传递图，根据这个图可以求出偏差E对于任意权值k的偏导数，例如当需要求出$ \frac{\partial E}{\partial k_{1-1}^2}$时，根据上图可以得到：

$$\frac{\partial E}{\partial k_{1-1}^2}=\frac{\partial E}{\partial x_1^3}\frac{\partial x_1^3}{\partial s_1^3}\frac{\partial s_1^3}{\partial k_{1-1}^2}$$

同理，当需要求出$ \frac{\partial E}{\partial k_{1-1}^1}$时，根据上图可以得到：

$$\frac{\partial E}{\partial k_{1-1}^1}=\frac{\partial E}{\partial x_1^3}\frac{\partial x_1^3}{\partial s_1^3}\frac{\partial s_1^3}{\partial x_1^2}\frac{\partial x_1^2}{\partial s_1^2}\frac{\partial s_1^2}{\partial k_{1-1}^1}+\frac{\partial E}{\partial x_2^3}\frac{\partial x_2^3}{\partial s_2^3}\frac{\partial s_2^3}{\partial x_1^2}\frac{\partial x_1^2}{\partial s_1^2}\frac{\partial s_1^2}{\partial k_{1-1}^1}$$

其他的权重的偏导数可以类比上述两个式子得到，当关于所有的权值的偏导数都得到后，组成的向量就是偏差在当前位置处的梯度。根据梯度就能不断靠近偏差的最小值点，从而得到满意的输出。

这里仔细观察上述的链式法则的变量传递图，可以发现一个有趣的事情，当我们把如图所示的部分视为一个新的神经元的话，整个链式法则就像是把神经网络反向一样，变成了一个2-4-(3)的神经网络。

实际上反向传递就是这么来的，神经网络通过对误差的反向传递得到对于所有权值的偏导，即当前的梯度，然后通过反向梯度的方法得到最优解。

读到这里应该已经对3-4-2的神经网络具体怎么工作有了一个概念，那么接下来要由特殊推至一般，得到任意架构的神经网络其梯度的算法。首先是对于三层的a-b-c的神经网络，上述过程的描述：

上面已经推导出了正向传递时的a-b-c的神经网络的关系方程：

第2层第j个神经元：

$$s_j^2=\sum _{i=1}^a{x}_i^1\ast k_{i-j}^1$$

$$x_j^2=f(s_j^2)$$

第3层第k个神经元：

$$s_k^3=\sum _{j=1}^b{x}_j^2\ast k_{j-k}^2$$

$$x_k^3=f(s_k^3)$$

偏差：

$$E=\frac{1}{2}\sum _{k=1}^c(x_k^3-y_k{)}^2$$

对于任意的第二层第j个神经元到第三层第k个神经元的权值$k_{j-k}^2$的偏导数$ \frac{\partial E}{\partial k_{j-k}^2}$，有：

$$\frac{\partial E}{\partial k_{j-k}^2}=\frac{\partial E}{\partial x_k^3}\frac{\partial x_k^3}{\partial s_k^3}\frac{\partial s_k^3}{\partial k_{j-k}^2}$$

这里已知：

$$\frac{\partial E}{\partial x_k^3}=x_k^3-y_k$$

$$\frac{\partial x_k^3}{\partial s_k^3}=f^{\prime }(s_k^3)$$

$$\frac{\partial s_k^3}{\partial k_{j-k}^2}=x_j^2$$

带入到上式中可以得到：

$$\frac{\partial E}{\partial k_{j-k}^2}=(x_k^3-y_k)\ast f^{\prime }(s_k^3)\ast x_j^2$$

同理对于第一层的第i个神经元到第二层的第j个神经元的权值$k_{i-j}^1$的偏导数，有：

$$\frac{\partial E}{\partial k_{i-j}^1}=\sum _{k=1}^c(\frac{\partial E}{\partial x_k^3}\frac{\partial x_k^3}{\partial s_k^3}\frac{\partial s_k^3}{\partial x_j^2}\frac{\partial x_j^2}{\partial s_j^2}\frac{\partial s_j^2}{\partial k_{i-j}^1})$$

这里已知：

$$\frac{\partial s_k^3}{\partial x_j^2}=k_{j-k}^2$$

$$\frac{\partial x_j^2}{\partial s_j^2}=f^{\prime }(s_j^2)$$

$$\frac{\partial s_j^2}{\partial k_{i-j}^1}=x_i^1$$

带入上式可以得到：

$$\frac{\partial E}{\partial k_{i-j}^1}=\sum _{k=1}^c[(x_k^3-y_k)\ast f^{\prime }(s_k^3)\ast k_{j-k}^2\ast f^{\prime }(s_j^2)\ast x_i^1]$$

到这里，仔细观察上述得到的两个一般情况下的权值的偏导数，可以看出来，假设将$ (x_k^{3-y_k)$看成输入，将$f’(s_k}3 )$看成函数处理，将$k_{j-k}^2$看成两细胞之间的权值，那么整个方程就可以看做是：

上一层的某一个神经元输入是$ (x_k^{3-y_k)$，经过该神经元$f’(s_k}3 )$的函数处理后，得到该神经元的输出，输出结果乘两神经元之间的权值$k_{j-k}^{2$是加权后的输出，所有加权后的输出结果的和就是$\sum_{k=1}}c [ (x_k^{3-y_k)*f’(s_k}3 )*k_{j-k}^2]$，也就是下一层的某个神经元的输入，再经过该神经元f^{\prime }(s_j^2)的处理得到$ \sum_{k=1}^c [ (x_k^{3-y_k)*f’(s_k}3 )*k_{j-k}^2]*f’(s_j2 )$…这个过程和前面所提到的神经网络的正向传递的步骤很相似，所以可以想到通过什么方法将正向和反向两个过程结合在一个神经网络的结构下。

这里仔细观察上一段话的描述，可以发现，如果我在神经元细胞中增加一个反向的通道，通道的输入是误差（对于输出层的神经元来说）或者上一层神经元的输出的加权和（对于隐层的神经元来说），函数处理是该神经元的$f^{\prime }()$，那么可以得到以下神经元的模型：

如图所示，虚线表示两个神经元之间的联系程度，即权值，s表示正向通道的加权和，即该神经元正向通道的输入，x表示正向通道的输出；t表示反向通道的加权和，即该神经元反向通道的输入，y表示反向通道的输出，则有一个神经元细胞有如下关系式：

正向通道：

$$s_j^M=\sum _{i=1}^a{x}_i^L{k}_{i-j}^{L-M}$$

$$x_j^M=f(s_j^M)$$

反向通道：

$$t_j^M=\sum _{k=1}^c{y}_k^N{k}_{j-k}^{M-N}$$

$$y_j^M=f^{\prime }(s_j^M)\ast t_j^M$$

该神经元左边任意一个权值的偏导数（因为反向传递时假如每一层都能得到该层左边的权值的偏导数，从输出层一层一层依次计算，就能得到全部的权值的偏导数）：

$$\frac{\partial E}{\partial k_{i-j}^{L-M}}=y_j^M\ast x_i^L$$

到这里，一个神经元已经可以搭建了，只要每个神经元都能实现上述正向通道、反向通道、权值偏导数计算即是一个合格的神经元，再将多个神经元组合成一层层的神经元层，再将各层之间进行连接，就得到了一个神经网络。这就是一个神经网络搭建的过程。

然后再提一点，就是在用Matlab搭建的时候，可以把每一层当做一个向量A、B…然后两层之间的权值写作一个矩阵，例如如果某一层的神经元个数为3，下一层为4，那么A=[1$$3]的向量，B=[1$$4]的向量，两层之间的权值矩阵是K_{A}B=[3$*$4],则有
$$A_{out}\ast K_{AB}=B_{in}$$
即A层的输出乘以权值矩阵等于B层的输入。

具体工程实例的搭建笔者已经根据上述内容自己写了一个Matlab神经网络的实例，在我的资源里可以下载MATLAB BP神经网络

或者不怕麻烦的话把下面的代码依次保存成.m文件，存到一个文件夹里，找到main.m文件执行。

1.main.m

P=[3,3,3,2];
learn=0.3;
net=net_int(P,learn);
OUTPUT=[0.2,0.4];
out=net_work(net,OUTPUT,1000);  

2.guiyi.m

function PN=guiyi(P,Pmin,Pmax,PNmin,PNmax)
PN=((P-Pmin)/(Pmax-Pmin))*(PNmax-PNmin)+PNmin;
end

3.layer_backward_input.m

        function a=layer_backward_input(a,b,K_ab);
            a.backward_in=b.backward_out*K_ab.matrix';
        end

4.layer_forward_input.m

        function b=layer_forward_input(a,b,K_ab);
            b.forward_in=a.forward_out*K_ab.matrix;
        end

5.layer_int.m

function layer=layer_int(number,mod,function_mod)
    layer=neuralnetwork_layer;
            layer.cell_number=number
            layer.forward_in=zeros(1,number)
            layer.forward_out=zeros(1,number)
            layer.backward_in=zeros(1,number)
            layer.backward_out=zeros(1,number)
            layer.backward_function=zeros(1,number)
    layer.mod=mod;
    layer.function_mod=function_mod;    
end

6.net_int.m

function net=net_int(P,lea)

    
    net=neuralnetwork_net;
    net.layer(1)=layer_int(P(1),'inputlayer','null');   
    for i=2:1:(length(P)-1)
        net.layer(i)=layer_int(P(i),'hidlayer','logsig'); 
    end
    net.layer(length(P))=layer_int(P(length(P)),'outputlayer','logsig');  
    
    
    for i=1:1:(length(P)-1)
        net.K(i)=neuralnetwork_weights;
        net.K(i)=weights_int(net.K(i),net.layer(i),net.layer(i+1),lea);
    end
    
end

7.net_work.m

function out=net_work(net,OUTPUT,times)
tic
for i=1:1:times    
INPUT=[((sin(i/100))+1)/2,(sin(i/100+1)+1)/2,(sin(i/100+2)+1)/2];
% OUTPUT=[0.2,0.4];
  net.layer(1)=inputlayer_change_input(net.layer(1),INPUT);

  for j=2:1:(length(net.layer))
    net.layer(j)=layer_forward_input(net.layer(j-1),net.layer(j),net.K(j-1));
    net.layer(j)=layer_forward_output(net.layer(j));
  end
  
  out(i,:)=net.layer(length(net.layer)).forward_out;
  
  net.layer(length(net.layer))=turn_back(net.layer(length(net.layer)),OUTPUT);
  
  net.layer(length(net.layer))=layer_backward_output(net.layer(length(net.layer)));
  net.K(length(net.layer)-1)=weight_get_gradient(net.layer(length(net.layer)-1),net.layer(length(net.layer)),net.K(length(net.layer)-1))
  
  for j=(length(net.layer)-1):-1:2
      net.layer(j)=layer_backward_input(net.layer(j),net.layer(j+1),net.K(j));
      net.layer(j)=layer_backward_output(net.layer(j));
      net.K(j-1)=weight_get_gradient(net.layer(j-1),net.layer(j),net.K(j-1))
  end
      
  for j=1:1:length(net.K)  
      net.K(j)=weight_rebuild(net.K(j));
  end
toc
end

8.neuralnetwork_layer.m

classdef neuralnetwork_layer
% 变量名称：
%     1.cell_number 神经元数目
%     2.forward_in 输出矩阵[n*1] 默认3*1
% 
% 函数名称：
%     1.layer_change_cell_number(a,number)
%         功能：改变该层的细胞个数
%         变量：a 该层变量；number 细胞个数；
%     2.inputlayer_change_input(a,INPUT)
%         功能：改变输入层的输入
%         变量：a 该层变量；INPUT 要改变的矩阵；
% 



% 变量名称：
%     1.cell_number 神经元数目
%     2.function_mod 正向传递函数种类 'purelin'/'logsig'/'tansig' 默认'logsig'
%     3.forward_in 输入矩阵[n*1] 默认3*1
%     4.forward_in 输出矩阵[n*1] 默认3*1
%     5.backward_in 反向输入矩阵[n*1] 默认3*1
%     6.backward_out 反向输出矩阵[n*1] 默认3*1
%     7.backward_function 反向输出方程系数矩阵[n*1] 默认3*1
% 
% 函数名称：
%     1.layer_change_cell_number(a,number)
%         功能：改变该层的细胞个数
%         变量：a 该层变量；number 细胞个数；
%     2.layer_forward_output(a)
%         功能：正向传递时，对该层进行函数处理后得到输出矩阵
%         变量：a 该层变量；
%     3.layer_backward_output(a)
%         功能：反向传递时，对该层进行函数处理后得到输出矩阵
%         变量：a 该层变量；
%     4.layer_forward_input(a,b,K_ab)
%         功能：正向传递时，对上一层的输出乘以权值矩阵得到该层的加权和输入
%         变量：a 该层变量；b 上一层变量；K_ab a-b层之间的权值矩阵
%     5.layer_backward_input(a,b,K_ab)
%         功能：反向传递时，对上一层的输出乘以权值矩阵的转置得到该层的加权和输入
%         变量：a 该层变量；b 上一层变量；K_ab a-b层之间的权值矩阵
%     n.函数名称
%         功能：
%         变量：
%     n.函数名称
%         功能：
%         变量：
%     n.函数名称
%         功能：
%         变量：
%     n.函数名称
%         功能：
%         变量：



    properties
        cell_number=3      ;
        mod='hidlayer';
        function_mod='logsig'    ;
        forward_in=zeros(1,3);
        forward_out=zeros(1,3);
        backward_in=zeros(1,3);
        backward_out=zeros(1,3);
        backward_function=zeros(1,3);
    end
    
    
    methods
        
        function obj=layer_change_cell_number(obj,number);   
            obj.cell_number=number
            obj.forward_in=zeros(1,number)
            obj.forward_out=zeros(1,number)
            obj.backward_in=zeros(1,number)
            obj.backward_out=zeros(1,number)
            obj.backward_function=zeros(1,number)
        end
         
        function a=layer_forward_output(a);
            switch(a.function_mod)
                case 'logsig'
                    a.forward_out=(1+exp(-a.forward_in)).^(-1);
                    a.backward_function=(1+exp(-a.forward_in)).^(-1)-(1+exp(-a.forward_in)).^(-2);
                otherwise
                    a.forward_out=a.forward_in;
            end
        end
            
        function a=layer_backward_output(a);
            a.backward_out=a.backward_function.*a.backward_in;
        end
        
        function a=turn_back(a,OUTPUT);
            a.backward_in=(a.forward_out-OUTPUT);
        end
        
        function a=inputlayer_change_input(a,INPUT);
            a.forward_out=INPUT
        end

        
                                      
    end
end

9.neuralnetwork_net.m

classdef neuralnetwork_net
    

properties
        layer_number=1      ;
        function_mod=[]    ;
%         layer_in=neuralnetwork_inputlayer;
%         layer_hid=neuralnetwork_hiddenlayer;
%         layer_out=neuralnetwork_outputlayer;
        layer=neuralnetwork_layer;
        K=neuralnetwork_weights;
    end      
    
end

10.neuralnetwork_weights.m

classdef neuralnetwork_weights
    properties
        matrix;
        gradient_matrix;
        learning_speed;
    end
    
    methods
        function K_ab=weights_int(K_ab,a,b,number);
            K_ab.matrix=rand(a.cell_number,b.cell_number)
            K_ab.gradient_matrix=rand(a.cell_number,b.cell_number)
            K_ab.learning_speed=number;
        end
        
        function K_ab=weight_change(K_ab,M);
            K_ab.matrix=M;
        end
                
        function K_ab=weight_rebuild(K_ab);
            K_ab.matrix=K_ab.matrix-K_ab.learning_speed*K_ab.gradient_matrix;
        end
        
        function K_ab=weight_change_learning_speed(number);
            K_ab.learning_speed=number;
        end
        
    end
        
end
    
    
    
    
    
    
    

11.out_guiyi.m

function P=out_guiyi(PN,Pmin,Pmax,PNmin,PNmax)
P=(PN-PNmin)/(PNmax-PNmin)*(Pmax-Pmin)+-Pmin;
end

12.weight_get_gradient.m

        function K_ab=weight_get_gradient(a,b,K_ab);
            K_ab.gradient_matrix=a.forward_out'*b.backward_out;
        end

以上就是我自己用Matlab搭建的BP神经网络，其实在我看来不是最终版本，还有很多细节可以补充，但是已经是可以实现构造一个任意层数任意神经元个数的一个BP神经网络架构了。有愿意学习的同学可以下下来看一看，如果上面那些公式推导你能看懂的话，那我写的架构应该很容易能够理解了。

其实MATLAB里有很多已经做好的函数包。想直接用神经网络解决问题的话，还是直接用别人造好的轮子。想要自己造轮子的话，或者想要自己探索不一样的造轮子方法的话，倒是可以参考上面的代码。但是只是参考哈，因为我在具体用上面代码的时候，还是发现了许多需要改进的地方，但是最近在忙其他课题，还没有时间去改进。