笔者近两年在实际工作中发现,制造业场景中会有很多问题可以用到优化算法(或启发算法)来解决,遗传算法作为最典型的算法可以解决绝大部分优化问题。遗传算法思想本身并不复杂,但在不同的场景中,其算子可以多种多样。
今天想跟大家讨论的是编码问题;编码作为遗传算法最开始的算子,其作用非常关键;目前网上大部分资料都是用二进制方法来编码;前段时间我看到一些NLP的文章,了解到one-hot方法来表示特征;能不能用到遗传算法中呢? 因此我做了一个简单的遗传算法-onehot版本,实验了一下是可行的。
先将算法思想简单陈述一下:
一、编码:
加入待求变量X区间为[1:10],DNA_SIZE设为10,即10个基因位;在初始化的时候,随机选取1到10以内任意一个整数作为表征;比如下图中,第五个元素为1,即该染色体代表5
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
二、交叉:
父代染色体基因位求平均值,子基因位=(P1的基因位+P2的基因位)/2
比如下图中,P1基因位是2,P2基因位是9 ;子代基因位=(2+9)/2=5(取整)
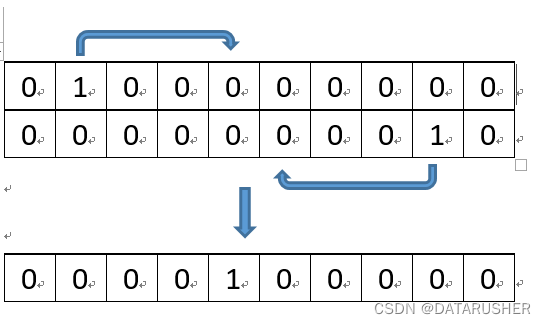
直观的表达就是: P1代表整数2,P2代表整数9,子代就是5
因为此方法编码的方式与传统的二进制编码不同,所以其交叉、变异算子也会不同;为什么交叉要取父代的平均值,因为这样可以大范围搜索解空间
三、变异
常规的二进制遗传算法中,变异算子通常是某个基因位变为0或1;本文中的变异算子为:向前或向后移动一位,比如某染色体基因位是8,根据随机数判断是向前还是向后移动一位,如果是向前移动一位,则变成8-1=7,如果是向后移动,则表示8+1=9;这个操作在交叉的基础上可以小范围精确搜索解空间
四、解码
解码即直接找到1所在元素的索引
其他算子逻辑与常规的算法逻辑相同
下面贴出实现代码:
其中 问题函数为:F(x)=x**2+1/x-9*x;x=[1:10],求F(x)最大值, 肉眼可知x=10时F(x)最大
import numpy as np
import random
from matplotlib import cm
#from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
DNA_SIZE = 10
POP_SIZE = 20
CROSSOVER_RATE = 0.3
MUTATION_RATE = 0.2
N_GENERATIONS = 30
X_BOUND = [0, 10]
k=2 #锦标赛 每次取K个染色体比赛
def fuc(x): #问题函数
return int(x**2+1/x-9*x)
def get_fitness(pop):#对种群每个个体打分
x=decode(pop)
result=[]
for i in range(len(pop)):
pred=fuc(x[i])
result.append(pred)
return result
def find_index(array): #找索引
count=0
for i in array:
count=count+1
if i==1:
break
count_back=count-1
return count_back
def decode(pop): #解码
x=[]
for i in pop[:]:
#i1=i.tolist()
z=find_index(i)+1
x.append(z)
return x
def crossover_and_mutation(pop,CROSSOVER_RATE,MUTATION_RATE):
new_pop = []
for father in pop:
child=[i for i in father]
if np.random.rand() < CROSSOVER_RATE: #交叉:父代交叉取索引之和除以2,相当于是找他们俩中间的数
mother = pop[np.random.randint(POP_SIZE-1)]
new_index=(find_index(father)+find_index(mother))/2
new_index=round(new_index)
child[find_index(child)]=0
child[new_index]=1
if np.random.rand() < MUTATION_RATE: #变异,-1或+1
if np.random.rand()<0.5:
if find_index(father)==0:
child[0]=1
else:
child[find_index(father)-1]=1
child[find_index(father)]=0
else:
if find_index(father)==len(child)-1:
child[-1]=1
elif find_index(father)<len(child)-1:
child[find_index(father)+1]=1
child[find_index(father)]=0
new_pop.append(child)
return new_pop
def select_run(pop, k): #锦标赛,随机取K个数,最大的放进赢家池
seq=[]
win=[]
for j in range(POP_SIZE):
r=random.sample(range(POP_SIZE),k)
for i in list(r):
seq.append( pop[i])
seq_fit=get_fitness(seq)
max_fitness_index = np.argmax(seq_fit)
win.append(seq[max_fitness_index])
seq=[]
return win
def print_info(pop,n):#打印出最优解
na.append(n)
fitness = get_fitness(pop)
max_fitness_index = np.argmax(fitness)
print("epo:", n)
print("max_fitness:", fitness[max_fitness_index])
x = decode(pop)
print("(最优解):", (x[max_fitness_index]))
best.append(x[max_fitness_index])
plt.figure(figsize=(10,8), dpi=80)
plt.plot(na,best)
plt.show()
n=0
na=[]
best=[]
pop=np.random.randint(1, size=(POP_SIZE, DNA_SIZE*10)) #初始化种群
for x in range(POP_SIZE):
r=np.random.randint(0, DNA_SIZE*10)
pop[x][r]=1
for _ in range(N_GENERATIONS):#迭代N代
n=n+1
pop_new=select_run(pop,k) #锦标赛生成新的种群
new_pop=crossover_and_mutation(pop_new,CROSSOVER_RATE,MUTATION_RATE)#交叉变异
print_info(new_pop,n)
pop=[i for i in new_pop] #更新种群进入下一次迭代
代码说明:
DNA_SIZE = 10 ;染色体长度为10,但是在代码中,我把长度做了处理(DNA_SIZE*10)相当于是100,虽然解的范围还是【1,10】但是其精确度可以达到0.1,如果长度变为1000,精确度达到0.01
POP_SIZE = 20 ;染色体数量
CROSSOVER_RATE = 0.3 ;交叉概率
MUTATION_RATE = 0.2 ;变异概率
N_GENERATIONS = 30 ;迭代次数
X_BOUND = [0, 10] ;X的取值范围
k=2 ;选择算子使用锦标赛来淘汰不佳的染色体,k表示每次比赛选几个染色体来PK
运行结果:
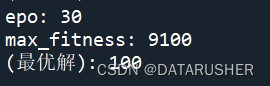
横轴代表迭代次数;纵轴代表X的值
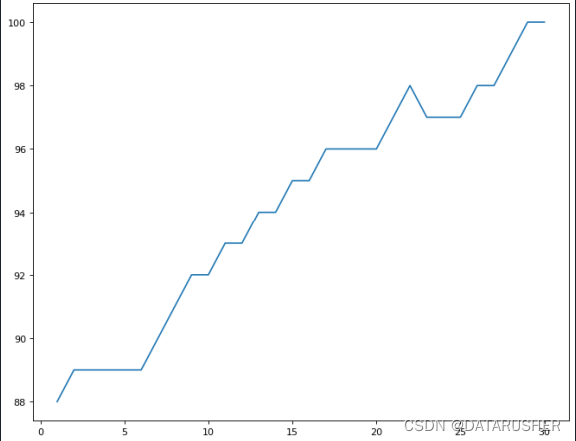
第29代即可收敛
总结:
1、代码运行慢,里面有很多重复的变量、for循环,后期改进时可以提高代码质量
2、运行效果,并不是每次都是30代收敛,有的需要50代以上,说明交叉、变异算子还有优化的空间;下一步可以借鉴动量梯度下降法的思想,在迭代初期可以把移动步幅变大,比如每次移动三步,在迭代后期减小移动步幅
3、one-hot虽然比较直观,但是如果问题函数的精确度要求比较高,染色体长度会变长,搜索效率会变低,可能不如二进制编码好





 本文探讨了将one-hot方法用于遗传算法编码的可行性。介绍了遗传算法one-hot版本的编码、交叉、变异、解码算子,给出实现代码及运行结果。指出代码存在运行慢、收敛不稳定等问题,还提到one-hot编码在高精度要求下搜索效率低,后续可借鉴动量梯度下降法优化。
本文探讨了将one-hot方法用于遗传算法编码的可行性。介绍了遗传算法one-hot版本的编码、交叉、变异、解码算子,给出实现代码及运行结果。指出代码存在运行慢、收敛不稳定等问题,还提到one-hot编码在高精度要求下搜索效率低,后续可借鉴动量梯度下降法优化。
















 1271
1271

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








